A型扩张仿射李代数的极大子代数
廖建玲,夏章生
(湖北民族学院 理学院,湖北 恩施 445000)
A型扩张仿射李代数的极大子代数
廖建玲,夏章生*
(湖北民族学院 理学院,湖北 恩施 445000)
摘要:设S是欧式空间n上的最小半格,由Jordan代数J(S)通过TKK构造可得到一个称之为TKK代数的李代数T(J(S)).进一步,可由TKK李代数T(J(S))得到一个A1型、零度为v,且带有扩张仿射根系R(A1,S)的扩张仿射李代数.研究了扩张仿射李代数的极大子代数,并得到了它的四类极大子代数.
关键词:扩张仿射李代数;TKK代数;半格;极大子代数
扩张仿射李代数,也称之为不可约拟单李代数,最初是由文献[1-2]的作者提出的,它是有限维单李代数,仿射Kac-Moody代数和Toroidal李代数的推广.文献[2]给出了带有任意的零度和一般扩张仿射根系结构的扩张仿射李代数L的一般结构,该扩张仿射李代数可从某个李代数G出发而得到.对于一个A1型、零度为v,且带有扩张仿射根系R(A1,S)的扩张仿射李代数,李代数G可以选择为一个Jordan代数J(S)通过TKK构造得到的称之为TKK代数的李代数T(J(S)),其中S是欧式空间n上的一个半格.在文献[3]中,TKK李代数通过另外一种新的方法得到:T(J(S))=sl2(⊗J⊕[LJ,LJ].在本文中将沿用这种新的结构.众所周知,从半格相似的意义来看,在2上,仅有两个非相似的半格,即一个非格的半格和格2.在文献[3-4]中,作者分别研究了与两个半格相关的TKK李代数和它们的顶点算子表示.在文献[5]中,作者研究了TKK李代数T(J(2)),并给出了它的2-阶化自同构群.类似地,在文献[6]中,本文作者研究了n上的最小半格(S0+ei)对应的TKK李代数T(J(S)),并得到它的n-阶化自同构群及其结构分解,其中S0=2n,e0=0,ei是n中第i个分量为1,其余分量全为0的单位向量.本文研究了由这个TKK李代数T(J(S))得到的扩张仿射李代数,并给出了它的四类极大子代数.为方便计,首先给出相关符号说明:将用和分别表示整数集和复数集,用x+=e12,x-=e21和h=e11-e22分别表示单李代数sl2()的Chevalley基.
1A1型的扩张仿射李代数
首先回顾一下文献[2]中有关扩张仿射李代数的一些基本概念.
1)S是离散的,
3)0∈S,-S=S,且S+2S⊆S.
进一步,若用S+S⊆S代替S+2S⊆S,上述其他条件也成立时,则称S是n上的一个格.设S和S′是n上两个半格,如果存在n的一个线性自同构φ,使得φ(S)=S′,则称S和S′是同构的,记为S≅S′;如果存在σ′∈S′,使得S≅S′+σ′,则称S和S′是相似的.
根据半格的相关性质,在文献[2]中作出了如下假定:在相似的意义下,一般将n上的每一个半格S认定成n关于子群2n的若干陪集的并,而且包含着平凡陪集2n,以及由S生成的子群〈S〉=n.
则J是一个含有单位元1=x0的Jordan代数.
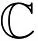
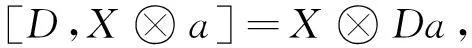
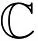
因此,TKK代数T是n-阶化的:,其中:
(1)
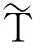
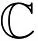
其中σ∈S,则在[LJ,LJ]上存在一个不变的对称双线性型(·,·)[2],使得:(D,[La,Lb])=η((Da)·b),
其中D∈[LJ,LJ],a,b∈J.特别地,对于任意的σ,τ∈I,(D(σ),D(τ))=4δσ+τ,0.
可以将此双线性型扩充成T上一个不变的对称双线性型(·,·):
(X⊗a+D1,Y⊗b+D2)=(X,Y)η(a·b)+(D1,D2)
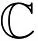
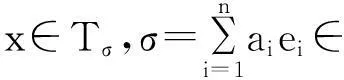
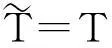
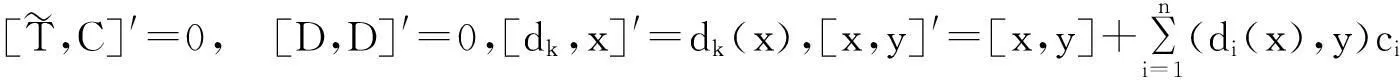
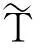
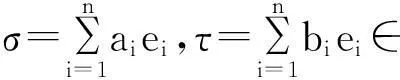
(2)
(3)
(4)
(5)
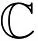
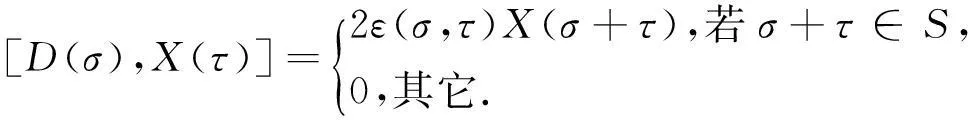
(6)
(7)
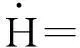
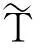
定理2M是H-阶化的.
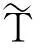
定理2的另一说法是,M的每一个元素的阶化分量也是属于M的,比如:若2x+(σ1)+3x+(σ2)-3x-(σ3)+5h(σ4)-7D(τ5)∈M,则x+(σ1),x+(σ2),x-(σ3),h(σ4),D(τ5)∈M.
为此,定义下述记号:
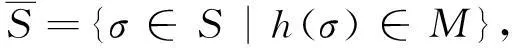
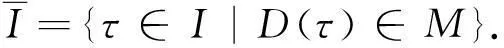
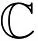
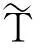
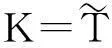
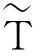
定理3中的两个极大子代数,分别满足S+=∅和S-=∅.由此,下文中将假定:S+≠∅且S-≠∅.
证明因为S+≠∅且S-≠∅,取σ∈S+,σ′∈S-.则有下面5种情况:
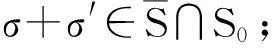
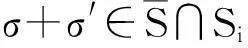
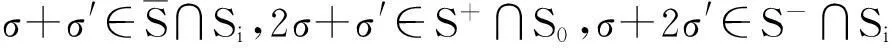
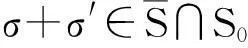
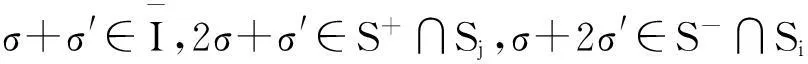
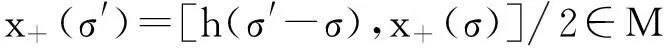
类似地,S-是2n在n中的某个陪集的并集.根据引理2:对于每个i=0,1,…,n,S+∩Si≠∅当且仅当S-∩Si≠∅,可得S+=S-.证毕.
定理4设J1,J2是{1,2,…,n}的两个互补的子集,且J2≠∅,则:
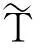
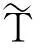
若J1≠∅,有下述三种情况:
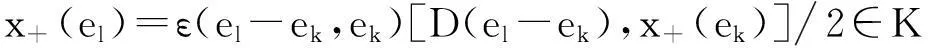
2)若存在某个h(σ0)∈K,其中σ0∈Sk,k∈J2,则由x+(0)∈M3⊆K,可得:
再由情况(1)可推知对任意k∈J2,x+(ek)∈K;
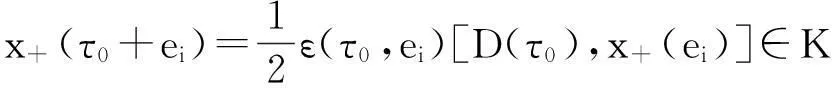
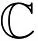
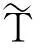
定理5设J1,J2是{1,2,…,n}的两个互补的子集,且J1≠∅,则:
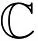
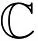
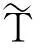
若J2≠∅,分下述三种情况来分析:
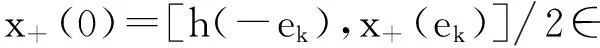
2)若存在某个h(σ0)∈K,其中σ0∈Sk,k∈J1,则因x+(-σ0)∈M4⊆K,有:
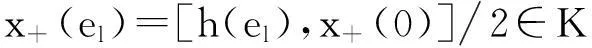
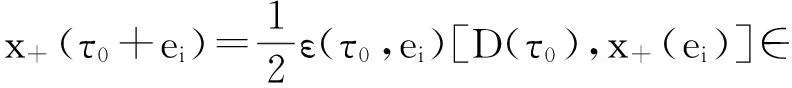
另一方面,若J2=∅,则:
并且K必包含某个x+(σ1)或x-(σ1)或h(σ2),其中σ1∈S0,σ2∈Sk,k∈J1={1,2,…,n}.同样由情况(1)和情况(2)可得,对任意k∈J2,x+(ek)∈K.
参考文献:
[1]RHoegh-Krohn,BTorresani.Classificationandconstructionofquasi-simpleLiealgebras[J].JournalofFunctionalAnalysis,1990,89:106-136.
[2]BAllison,NAzam,SBerman,etal.ExtendedaffineLiealgebrasandtheirrootsystems[M].MemoirsoftheAmericanMathematicalSociety,1997.
[3]STan.TKKalgebrasandvertexoperatorrepresentations[J].JournalofAlgebra,1999,211:298-342.
[4]XMao,STan.VertexoperatorrepresentationsforTKKalgebras[J].JournalofAlgebra,2007,308:704-733.
[5]CYe,STan.GradedautomorphismgroupofTKKalgebra[J].ScienceinChina,SeriesA,2008,51:161-168.
[6]ZXia.GradedautomorphismgroupofTKKLiealgebraoversemilattice[J].ActaMathematicaSinica,EnglishSeries,2011,27:537-544.
[7]VGKac.InfinitedimensionalLiealgebras[M].CambridgeUniversityPress,1988.
责任编辑:时凌
Maximal Subalgebras of Extended Affine Lie Algebra of Type A
LIAO Jianling,XIA Zhangsheng*
(School of Science,Hubei University for Nationalities,Enshi 445000,China)
Abstract:Let be the extended affine Lie algebra of type A1 and of nullity v with extended affine root system R(A1,S),which is constructed from a TKK Lie algebra T(J(S))obtained from the Jordan algebra J(S) by the so-called Tits-Kantor-Koecher construction,where S is the ″smallest″ semilattice in Euclidean spacen.In this paper,we study maximal subalgebras of extended affine Lie algebra and obtain four kinds of maximal subalgebras.
Key words:extended affine Lie algebra;TKK Lie algebra;semilattice;maximal subalgebra
收稿日期:2016-02-13.
基金项目:国家自然科学基金项目(11126078,11571145);湖北省教育厅科研项目(Q20122906).
作者简介:廖建玲(1979- ),女,硕士生,主要从事李代数的研究;*通信作者:夏章生(1978- ),男,博士,副教授,主要从事李代数的研究.
文章编号:1008-8423(2016)01-0024-05
DOI:10.13501/j.cnki.42-1569/n.2016.03.006
中图分类号:O152.5
文献标志码:A

