基于非合作博弈的应急车辆调度与再配置*
赵建东 段晓红 宋守信
(1.北京交通大学 机械与电子控制工程学院, 北京 100044;2.北京交通大学 经济管理学院, 北京 100044)
基于非合作博弈的应急车辆调度与再配置*
赵建东1段晓红1宋守信2
(1.北京交通大学 机械与电子控制工程学院, 北京 100044;2.北京交通大学 经济管理学院, 北京 100044)
摘要:多事故多救援站点的应急车辆调度问题中,在处置当前事故时,若将空闲车辆再配置于救援站点,有利于对潜在事故的快速响应.文中采用双层规划理论和非合作博弈理论建立应急车辆调度与再配置模型.上层模型在事故需求和救援时间窗约束下,最小化当前事故响应时间;下层模型将各救援站点视为非合作博弈的局中人,综合考虑车辆再配置时间和救援站覆盖区域潜在风险,确定局中人的收益函数,将优化再配置策略转化为寻求非合作博弈的纳什均衡.然后,提出一种层次混合蛙跳算法,其中上层算法用于求解约束单目标规划问题,下层算法用于求解非合作博弈模型.求解事故算例证明了应急车辆调度与再配置模型的合理性和层次混合蛙跳算法的有效性.
关键词:应急车辆;调度算法;资源配置;博弈论
高速公路里程和路网密度的迅速增加、交通出行量和交通事故发生频率的急剧上升、交通安全形势的日趋严峻,对快速高效的事故应急救援能力提出了迫切需求.科学合理地调度有限的应急车辆是应急救援的关键问题,可有效减少事故损失.
目前,应急车辆调度研究主要集中在调度建模方法和调度求解算法.调度建模方面,Yamada[1]提出仅考虑当前事故救援需求,应急资源调度决策可转化为路网最短路的求解,以选择事故最近出救点.何建敏等[2]针对单事故下多出救点选择问题,引入时间最短的概念,提出了单目标、多目标等多种组合优化模型.戴更新等[3]将单资源调度扩展到多资源调度,以救援起始时间最早为目标,建立了多资源调度数学模型.Carter等[4]指出考虑未来事故需求,选择离事故点最近的出救点不一定是最优策略.Sherali等[5]将资源调度总成本定义为当前事故救援成本和潜在事故救援机会成本的总和,建立了应急车辆调度的机会成本法模型.Ozbay等[6]针对潜在事故资源需求的随机性,引入服务质量概念,建立了一种带有概率型约束的整数规划模型,用以解决交通事故响应和资源调配问题.Zhao等[7]针对机会成本模型中车辆速度和潜在事故概率的不确定性问题,引入削弱救援车速系数概念,修正了机会成本模型中的速度参数.杨继君等[8]研究了在应急资源有限条件下的多灾点资源调度问题,考虑到各灾点利益的冲突性,建立了基于非合作博弈的应急资源调度模型.Yang等[9]建立了带区域覆盖约束的应急优化车辆调度模型,通过将空闲车辆重新配置于各救援站点的方法避免对潜在事故的救援延迟.
调度求解算法方面,Chang等[10]提出一种基于贪婪搜索的多目标遗传算法,自动生成多种可行的应急物资调度策略.Ichoua等[11]应用并行禁忌搜索算法,分别求解了基于静态和动态参数的车辆调度模型.刘芹等[12]设计了一种混合粒子群算法来实现车辆调度模型的求解.杨仁法等[13]运用蚁群算法把时间窗约束转化为惩罚函数形式,求解了带时间窗约束的配送中心车辆调度问题.
综述文献,国内外学者在应急车辆调度建模时已考虑车辆再配置.笔者在文献[14]中提出将救援站覆盖区域潜在风险作为关键约束,建立了应急车辆调度与再配置的多目标规划模型.接着,在文献[15]中分析了应急车辆调度和再配置两类目标间的层级关系,建立了双层规划模型.模型以当前事故响应时间最短为上层目标,应急车辆再配置时间最短为下层目标.进一步分析文献[8]、[16-17]发现,非合作博弈理论在求解资源限制条件下的多灾点应急资源调度、作业车间任务调度及出租车调度等竞争问题时均体现了考虑各局中人之间利益冲突的优点.因此,在文献[14-15]的研究基础上,文中提出应用非合作博弈理论求解下层应急车辆再配置过程中的冲突问题.通过将各个救援站视为博弈模型的局中人,可能的车辆再配置方案映射为策略集,从而将应急车辆再配置问题转化为对非合作博弈模型的纳什均衡点求解.此外,还设计了一种层次混合蛙跳算法实现模型求解.
1问题描述


图1 多事故多救援点应急车辆调度问题Fig.1 Emergency vehicle scheduling problem with multiple accidents and multiple rescue sites
2模型构建
路网内应急车辆储备有限,导致当前事故救援需求和潜在事故储备之间存在着竞争关系.应急车辆应优先调度至事故点,以救援当前事故.当前事故救援策略可指导以保证潜在事故资源储备为目标的应急车辆再配置决策.同时,应急车辆调度决策也需兼顾考虑车辆再配置选择.据此,文中将当前事故救援问题作为上层问题,应急车辆再配置问题作为下层问题,建立双层规划模型.
2.1上层模型构建
2.1.1 上层目标函数
事故响应时间是调度决策的关键因素,事故响应时间由调度决策时间与车辆在途时间构成[5],上层目标函数用于最小化车辆在途时间:
(1)
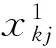
2.1.2上层约束条件
(1)事故需求约束
前往事故ej的车辆总和与事故ej的需求Nj相一致:
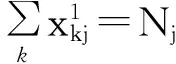
(2)
(2)救援时间窗约束
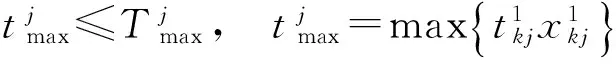
(3)

(4)
2.2下层模型构建
在路网内应急车辆有限的情况下,各个救援站所需资源是相互冲突的,各方利益相互影响,一方利益的增加必然导致其他救援站利益的减少.从博弈论角度来看,各救援站间潜在事故对应急车辆的需求可认为是非合作博弈的,博弈的目的是尽量为自身争取更合理的效用,即以更少的成本获得更多的资源.
(1)策略集

(5)
(2)效用函数

(6)

2.2.1下层目标函数
定义1策略组合X2*是I人非合作博弈的一个纳什均衡解,如果X2*满足:
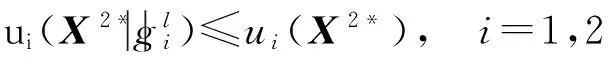
(7)

在应急车辆再配置问题中,每一个救援站si从其策略集Gi中选取某一种策略,组成I人博弈的策略组合X2.根据纳什均衡定义,下层目标函数为
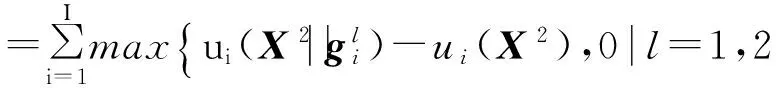
(8)
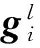
2.2.2下层约束条件
应急车辆vk可以派往当前事故点或者再配置于救援站点,且只能处于两种状态之一:
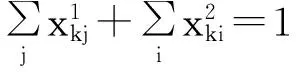
(9)
3基于层次混合蛙跳算法的车辆调度模型求解
混合蛙跳算法(SFLA)是一种模因元启发式算法,采用混合进化算法(SCE)的全局寻优策略和粒子群算法(PSO)的局部迭代规则.算法基于族群内个体模因进化和种群中全局信息交流,将青蛙种群分为多个族群,各族群内青蛙通过信息交换实现局部深度进化.一段时间后,将各子族群混合,使信息在整个种群内得到交流.各子族群内局部寻优和全局信息融合往复执行至达到指定进化代数.

(10)
其中,Mo表示第o个族群.
根据式(11)及(12),各子族群中的最差青蛙位置W跟随族群内最优青蛙位置Y或种群最优青蛙位置Z进行局部更新,直到完成指定迭代次数α.
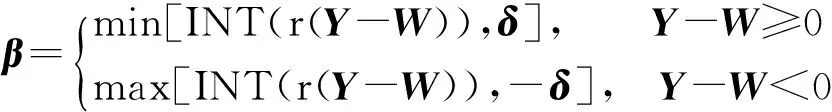
(11)
Wnew=Wold+β
(12)
其中,r为一随机数且r∈[0,1],β表示青蛙个体的调整矢量,δ表示最大调整步长,Wold和Wnew分别为更新前、后的最差青蛙位置 .
完成局部搜索的各族群重新混合,排序后执行下一次分组及局部搜索,直至完成指定的外层迭代次数η.
3.1求解非合作博弈模型的混合蛙跳算法
求解非合作博弈模型的混合蛙跳算法中,每只青蛙的位置g=(g1,g2,…,gI),gi∈Gi,1≤i≤I,代表I人博弈的一个策略组合.青蛙群体在策略组合空间中寻找最优位置,青蛙位置的优劣由适应度函数反应,当青蛙处于最优位置时对应的适应度函数到达最大.与目标函数相一致,应急车辆再配置问题的适应度函数定义为


(13)
3.2求解双层规划问题的层次混合蛙跳算法
采用与文献[15]相同的双层架构,设计求解应急车辆调度与再配置的层次混合蛙跳算法.该架构集成了两个基本混合蛙跳算法模型SFLA_U及SFLA_D.
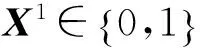


3.2.1编码方案设计

X(χ,:)=[xχ,1,xχ,2,…,xχ,k,…,xχ,K]
(14)

3.2.2适应度函数设计


(15)
ωj=ξj
(16)

(17)

(18)
式中,εj、ξj分别表示事故ej的现场疏散能力及事故严重程度.同文献[15],εj定义见表1.对应于事故由轻微到严重的4个等级,εj的取值依次为40、60、80、100.
表1时间窗约束惩罚
Table 1Punishment for time window constraints

被影响车道数目εjjmin1812.52616.7被影响车道数目εjjmin3425.0>3250.0
下层混合蛙跳算法SFLA_U用来求解基于非合作博弈论的应急车辆再配置模型,其适应度函数κD(X2)为
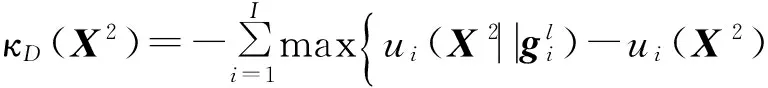
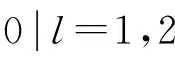
(19)
4算例分析
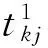
表2救援站参数
Table 2Rescue site parameters

si算例Ris1I25II21s2I22II24si算例Ris3I17II27s4I10II10
表3当前事故参数
Table 3Current accident parameters

ej算例NjξjεjTjmaxTjminωjjmaxjmine1I2604155606025.0II1408100404012.5e2I140880404012.5II16062010606016.7e3III1804156808025.0
表4车辆在途时间
Table 4Travel time matrix

应急车辆算例e1e2e3s1s2s3s4v1I810II6812010514v2I126II12814100128v3I612II713131111614v4I715II9167131209v5I1310II15149166155
根据决策变量规模大小,层次混合蛙跳算法参数选择如表5所示.运行层次混合蛙跳算法,经过寻优过程,获得两个算例的最优解如表6所示.表中包含有文献[15]原模型的最优解数据.并分别采用层次混合蛙跳算法(SFLA)和文献[18]中的层次粒子群算法(PSO)对两个算例进行求解,结果见表7.
表5层次混合蛙跳算法参数设置
Table 5Selection of parameters of integrated bi-level shuffled frog-leaping algorithm

算例上层种群规模上层族群数上层组内迭代次数上层全局迭代次数上层最大调整步长I30020155[6,6,6,6,6]II500252010[7,7,7,7,7]编号下层种群规模下层族群数下层组内迭代次数下层全局迭代次数下层最大调整步长I15015105[6,6,6,6,6]II15015105[7,7,7,7,7]
表6算例最优解
Table 6Optimal solutions of examples

算例上层目标最优值下层目标最优值最优解本模型原模型文中模型原模型文中模型原模型I19460.3733113,2,1,1,43,2,1,1,4II28570.1900154,5,1,3,21,5,2,3,6
表7层次混合蛙跳算法与层次粒子群算法的对比
Table 7Comparison of integrated bi-level shuffled frog-leaping algorithm and particle swarm optimization algorithm

算例最优解平均迭代次数求解时间/s10次运行中获得最优解的比例/%SFLAPSOSFLAPSOSFLAPSOSFLAPSOI3,2,1,1,45.342.68.5225.489050II4,5,1,3,26.851.315.0344.379050
4.1算例I的结果分析
文中模型获得的最优解均为[3,2,1,1,4],和原模型一样.最优调度与再配置策略如图2所示,表示应急车辆v1前往救援站s1,应急车辆v2前往事故点e2,应急车辆v3和v4前往事故点e1,应急车辆v5前往救援站s2.最优策略分析如下.

图2 最优调度与再配置策略Fig.2 Optimal scheduling and reallocation strategy
4.1.1对于事故e1的应急车辆调度策略
事故e1的应急车辆需求为2,将5辆车到达事故点e1的在途时间升序排列为(v3:6 min),(v4:7 min),(v1:8 min),(v2:12 min)和(v5:13 min).若将车辆v3和v4派往事故e1,则满足使应急车辆在途时间最小的上层目标.然而,在满足事故点e1应急车辆需求的同时,还应考虑事故点e2的需求及对各救援站的车辆再配置.假设选择次优策略,应急车辆v1代替v3或v4被派往事故e1,则增加了车辆在途时间的同时,也使对救援站s1的再配置时间延长了至少10 min.可见,将应急车辆v3和v4派往事故e1是合理的.
4.1.2对于事故e2的应急车辆调度策略
事故e2的应急车辆需求为1,将5辆车到达事故点e2的在途时间升序排列为(v2:6 min),(v1:10 min),(v5:10 min),(v3:12 min)和(v4:15 min).若将车辆v2派往事故e2,则满足使应急车辆在途时间最小的上层目标.假设选择次优策略,将车辆v1派往事故e2,则车辆在途时间增加了4 min,为保证对当前事故e2的快速救援,应将车辆v2派往事故e2.
4.1.3应急车辆再配置策略
由于应急车辆v2、v3和v4前往救援当前事故,空闲车辆为v1和v5.为分析下层模型的有效性,计算所有可能再配置策略对应的目标函数值,结果如表8所示.
表8再配置策略下层目标函数值
Table 8Performance function value of the second level of possible strategies
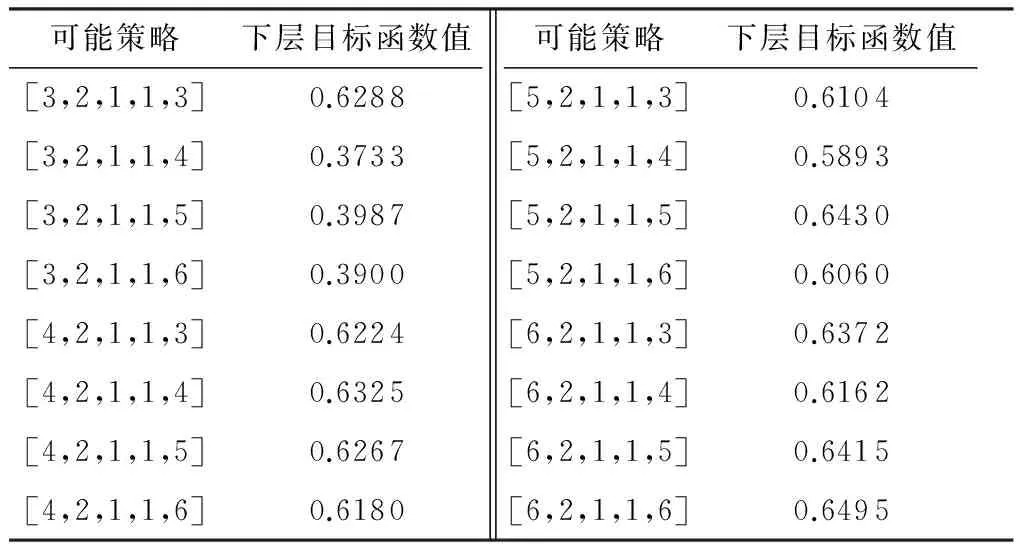
可能策略下层目标函数值[3,2,1,1,3]0.6288[3,2,1,1,4]0.3733[3,2,1,1,5]0.3987[3,2,1,1,6]0.3900[4,2,1,1,3]0.6224[4,2,1,1,4]0.6325[4,2,1,1,5]0.6267[4,2,1,1,6]0.6180可能策略下层目标函数值[5,2,1,1,3]0.6104[5,2,1,1,4]0.5893[5,2,1,1,5]0.6430[5,2,1,1,6]0.6060[6,2,1,1,3]0.6372[6,2,1,1,4]0.6162[6,2,1,1,5]0.6415[6,2,1,1,6]0.6495
由表可见,策略[3,2,1,1,4]的下层目标函数值最小,该策略更符合应急车辆调度与再配置模型的优化目标.
4.2算例II的结果分析
文中模型求得的最优解为[4,5,1,3,2],而原模型的最优解为[1,5,2,3,6],如表9所示,将最优解解码并进行比较.最优调度与再配置策略如图2所示,表示应急车辆v1前往救援站s1,应急车辆v2前往救援站s2,应急车辆v3前往事故点e1,应急车辆v4前往事故点e3,应急车辆v5前往事故点e2.
4.2.1对于当前事故的应急车辆调度策略
事故e1的应急车辆需求为1,将5辆车到达事故点e1的在途时间升序排列为(v1:6 min),(v3:7 min),(v4:9 min),(v2:12 min)和(v5:15 min).若将车辆v1派往事故e1,则满足使应急车辆在途时间最小的上层目标.假设选择次优的策略,应急车辆v3代替v1被派往事故e1,则当前事故e1的救援时间仅延长1 min,而对具有最高潜在风险的救援站s1的再配置时间缩短了10 min,可见,应该将应急车辆v3派往事故点e1.
同理,可证明对事故点e2和e3的调度策略是合理的.
4.2.2应急车辆再配置策略
由表9可知,文中模型求得最优策略的目标函数值较原模型优化了56%,说明策略[4,5,1,3,2]的整体效用比 [1,5,2,3,6]高,因此文中模型获得的策略更加合理.
表9算例II两种最优策略对比
Table 9Comparison of two optimum strategies of example II
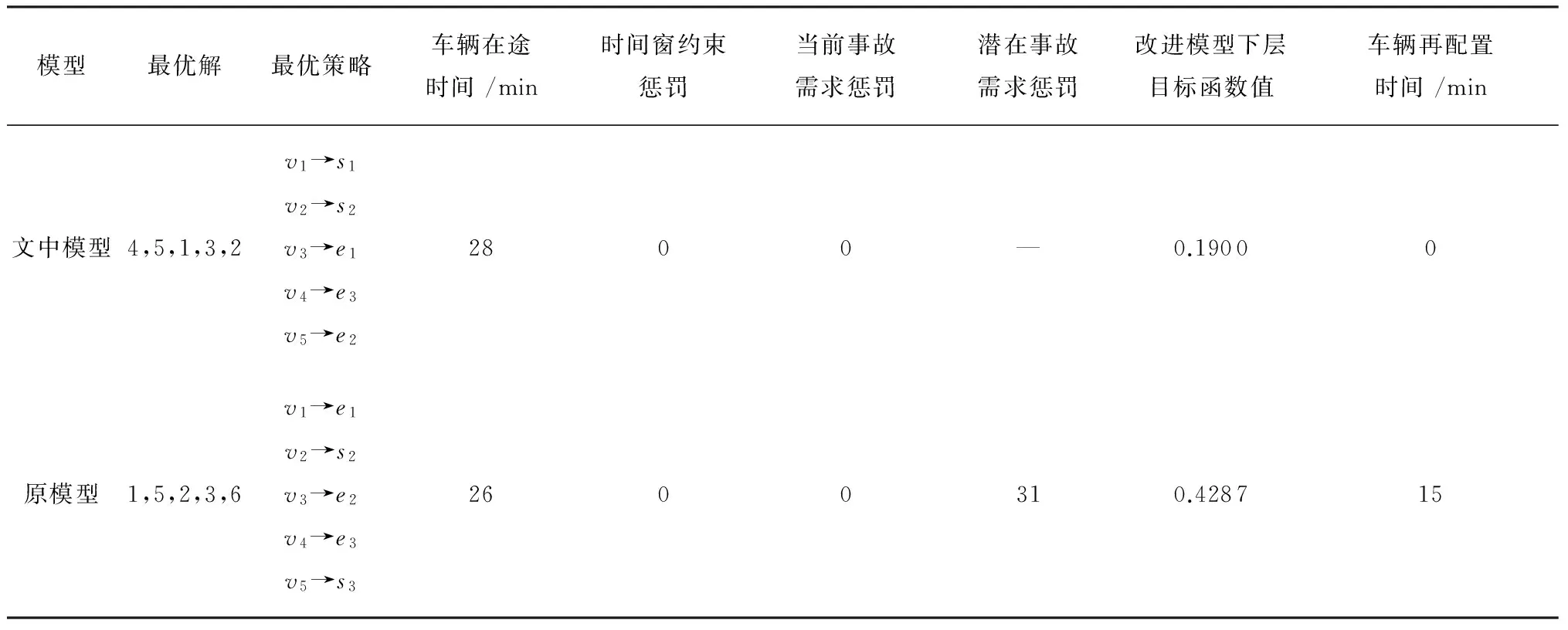
模型最优解最优策略车辆在途时间/min时间窗约束惩罚当前事故需求惩罚潜在事故需求惩罚改进模型下层目标函数值车辆再配置时间/min文中模型4,5,1,3,2v1→s1v2→s2v3→e1v4→e3v5→e22800—0.19000原模型1,5,2,3,6v1→e1v2→s2v3→e2v4→e3v5→s32600310.428715
4.3算法性能分析
表7中2个算例数据表明,层次混合蛙跳算法和层次粒子群算法在10次运行后均能获得最优解,层次混合蛙跳算法平均求解时间大约为层次粒子群算法的1/3;前者10次运行中获得的最优解比例高于后者.
5结语
事故发生后,调度应急车辆对当前事故进行有效救援的同时,综合考虑救援站覆盖区域潜在风险情况,对应急车辆进行统筹再配置,可以有效缩短对潜在事故的响应时间.文中基于应急车辆调度与再配置双层规划模型,考虑各救援站点对于有限资源的竞争关系,将各救援站点视为非合作博弈的局中人,定义了与再配置时间和救援站覆盖区潜在风险相关的收益函数,通过寻求多人非合作博弈的纳什均衡解获得优化的再配置策略;设计了一种层次混合蛙跳算法完成了模型的求解,上层算法采用基于权重的混合蛙跳算法模型,下层采用求解非合作博弈的混合蛙跳算法模型.模型的算例验证结果表明:文中双层规划模型符合应急车辆调度与再配置问题的决策规则;下层模型综合考虑应急车辆再配置时间和区域潜在风险,符合下层问题的决策目标;基于双层规划问题及非合作博弈问题求解思想设计的层次蛙跳算法,能较好地求解应急车辆调度与再配置模型,且在求解速度和准确度方面均优于层次粒子群算法.
参考文献:
[1]YAMADA Takeo. A network flow approach to a city emergency evacuation planning [J]. International Journal of Systems Science,1996,27(10):931-936.
[2]何建敏,刘春林,尤海燕. 应急系统多出救点的选择问题 [J]. 系统工程理论与实践,2001,21 (11):89-93.
HE Jian-min,LIU Chun-lin,YOU Hai-yan. Selection of multi-depot in emergency systems [J]. Systems Engineering—Theory and Practice,2001,21(11):89-93.
[3]戴更新,达庆利. 多资源组合应急调度问题的研究[J]. 系统工程理论与实践,2000,20(9):52-55.
DAI Geng-xin,DA Qing-li. The study of combinatorial scheduling problem in emergency systems [J].Systems Engineering—Theory and Practice,2000,20 (9):52-55.
[4]CARTER G M,CHAIKEN J M,IGNALL E. Response area for two emergency units [J]. Operations Research,1972,20(3):571-594.
[5]SHERALI H D,SUBRAMANIAN S. Opportunity cost-based models for traffic incident response problems [J]. Journal of Transportation Engineering,1999,125(3):176-185.
[6]OZBAY Kaan,XIAO Weihua. Probabilistic programming models for response vehicle dispatching and resource allocation in traffic incident management[C]∥Proceedings of the 83rdAnnual Meeting Compendium of Papers CD-ROM. Washington D C: Transportation Research Board,2004.
[7]ZHAO Jiandong,DUAN Xiaohong,ZHANG Lina,et al. Traffic emergency resources dispatch based on opportunity cost method with GA-BP optimization model [J]. Advances in Information Sciences and Service Sciences,2013,5(9):301-309.
[8]杨继君,许维胜,黄武军,等. 基于多灾点非合作博弈的资源调度建模与仿真[J]. 计算机应用,2008,28(6):1620-1623.
YANG Ji-jun,XU Wei-sheng,HUANG Wu-jun,et al. Modeling and analyzing of simulation based on non-coope-rative games for multiple emergency locations in resources scheduling [J]. Computer Applications,2008,28(6):1620-1623.
[9]YANG Saini,HAMEDI Masoud,HAGHANI Ali. Online dispatching and routing model for emergency vehicles with area coverage constraints [J]. Transportation Research Record,2005,1923:1-8.
[10]CHANG Fu-Sheng,WU Jain-Shing,LEE Chung-Nan,et al. Greedy-search-based multi-objective genetic algorithm for emergency logistics scheduling [J]. Expert Systems with Application,2014,41(6):2947-2956.
[11]ICHOUA Soumia,GENDREAU Michel,POTVIN Jean-Yves. Vehicle dispatching with time-dependent travel times [J]. European Journal of Operational Research,2003,144(2):379-396.
[12]刘芹,史忠科. 混合粒子群算法求解交通路网中的车辆调度问题[J]. 控制与决策,2006,21 (11):1284-1288.
LIU Qin,SHI Zhong-ke. Hybrid particle swarm algorithm for vehicle routing problem in road networks [J]. Control and Decision,2006,21 (11):1284-1288.
[13]杨仁法,龚延成. 带时间窗车辆调度问题的蚁群算法[J]. 交通运输工程学报,2009,9(4):71-74.
YANG Ren-fa,GONG Yan-cheng. Ant colony algorithm of vehicle scheduling problem with time windows [J]. Journal of Traffic and Transportation Engineering,2009,9(4):71-74.
[14]DUAN Xiaohong,SONG Shouxin,ZHAO Jiandong,et al. Emergency vehicle dispatching based on shuffled frog leaping algorithm [J]. Journal of Computational Information Systems,2013,9(24):9875-9884.
[15]DUAN Xiaohong,SONG Shouxin,ZHAO Jiandong. Emergency vehicle dispatching and redistribution in highway network based on bi-level programming [J]. Mathematical Problems in Engineering,2015,2015:1-12.
[16]周光辉,王蕊,江平宇,等. 作业车间调度的非合作博弈模型与混合自适应遗传算法[J]. 西安交通大学学报,2010,44(5):35-39.
ZHOU Guang-hui,WANG Rui,JIANG Ping-yu,et al. Non-cooperation game model and hybrid adaptive genetic algorithm for job-shop scheduling [J]. Journal of Xi’an Jiaotong University,2010,44(5):35-39.
[17]BAI R B,LI J W,Atkin J A D,et al. A novel approach to independent taxi scheduling problem based on stable matching [J]. Journal of the Operational Research Society,2014,65(10):1501-1510.
[18]赵志刚,顾新一,李陶深. 求解双层规划模型的粒子群优化算法[J]. 系统工程理论与实践,2007,27(8):92-98.
ZHAO Zhi-gang,GU Xin-yi,LI Tao-shen. Particle swarm optimization for bi-level programming problem [J]. Systems Engineering—Theory and Practice,2007,27(8):92-98.
Emergency Vehicle Scheduling and Reallocation on the Basis of Non-Cooperative Game
ZHAOJian-dong1DUANXiao-hong1SONGShou-xin2
(1.School of Mechanical and Electronic Control Engineering, Beijing Jiaotong University, Beijing 100044, China;2.School of Economics and Management, Beijing Jiaotong University, Beijing 100044, China)
Abstract:When an emergency vehicle scheduling problem involving multiple accidents and multiple rescue sites occurs, the response time of potential accidents can be shortened by redistributing idle emergency vehicles on rescue sites, in addition to optimizing the scheduling of vehicles for current accidents.This paper presents an improved model of emergency vehicle scheduling and reallocation on the basis of bi-level programming and non-cooperative game.The upper level of the model is established under the constraints of accident requirements and accident rescue window to minimize the response time for current accidents, while in the lower level of the model, each rescue site is treated as a participant in a non-cooperative game, the payoff function of each participant is determined after taking into account the reallocation time of the vehicle and the potential risks within the coverage area of each rescue site, so that the optimal reallocation strategy is transferred into Nash equilibrium in a non-cooperative game.Afterwards, an integrated bi-level shuffled frog-leaping algorithm is proposed, which contains an upper-layer algorithm for single-objective programming and a lower-layer algorithm for solving the non-cooperative game.Several illustrative examples verify the rationality of the proposed model and the effectiveness of the integrated bi-level shuffled frog-leaping algorithm.
Key words:emergency vehicles; scheduling algorithms; resource allocation; game theory
收稿日期:2015- 05-11
*基金项目:国家科技支撑计划项目(2011BAG07B05-2)
Foundation item:Supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China(2011BAG07B05-2)
作者简介:赵建东(1975-),男,博士,副教授,主要从事交通安全与控制研究.E-mail:zhaojd@bjtu.edu.cn
中图分类号:X951
doi:10.3969/j.issn.1000-565X.2016.03.016
——博弈论

