内外激励作用下多自由度齿轮系统的非线性动力学特性

向　玲， 贾　轶， 李媛媛， 冯晓冉, 高雪媛， 邸薇薇

(华北电力大学 机械工程系，河北 保定　071003)

内外激励作用下多自由度齿轮系统的非线性动力学特性

向玲， 贾轶， 李媛媛， 冯晓冉, 高雪媛， 邸薇薇

(华北电力大学 机械工程系，河北 保定071003)

采用周期扩大法，建立了齿轮副的六自由度非线性动力学模型，模型考虑了齿轮副间的时变啮合刚度、齿侧间隙、齿面摩擦等非线性因素；对模型中的相关周期项作傅里叶级数展开，并采用数值积分方法研究六自由度齿轮传动系统的运动随转速、支撑刚度的分岔特性。结合poincaré截面图、分岔图、FFT频谱及最大Lyapunov指数图，系统地分析了支撑刚度对齿轮系统的影响。结果发现，随着激励频率的提高，系统经过多次跳跃进入混沌，提高支撑刚度会使系统的跳跃点数目增加，并且使系统的混沌区减小且整体后移，致使系统推迟进入混沌；再者会使系统通向混沌的道路多样化，除了拟周期通道之外，还出现了激变性、阵发性的混沌道路及“周期5-拟周期-锁相-不稳定吸引子-混沌”的非常规混沌道路。另外支撑刚度的提高会使系统的1/2次谐振加强，致使谐振频率下的动态啮合力(DMF)增大，但会使一些混沌区的DMF逐渐减小，并且使啮合轮齿经历“双边冲击-单边冲击-无冲击”的状态变化。

齿轮副；非线性动力学；摩擦；间隙；支撑刚度

齿轮系统是机械系统的重要组成部分，长期以来，人们对齿轮传动系统的振动特性进行了各种各样的理论和实验研究，也不断揭示了齿轮系统的运行机理及存在的一些复杂的非线性现象。其中， Vaishya等[1]考虑了摩擦的影响，建立了一对齿轮副的单自由度非线性微分方程，并用floquet理论研究了摩擦对齿轮的动态响应及稳定性的影响。Li等[2]通过建立润滑模型引入了摩擦并研究了齿对表面粗糙度、润滑液温度等因素对直齿轮副稳态响应的影响。Wang等[3]研究了摩擦对单自由度直齿轮副分岔与混沌特性的影响，结果表明摩擦对系统的混沌振动有抑制作用。Morad等[4]用多尺度法研究了单自由度直齿轮副的振幅跳跃现象及主共振和次谐共振响应。张锁怀等[5]对齿轮-轴承系统进行了一系列的研究，用多种方法研究了齿侧间隙、转速、等参数对转子轴承系统响应的影响，揭示了系统响应存在复杂的非线性现象。张义民等[6]研究了转速和扭矩对单自由度齿轮副的稳态响应(动态传递误差)的影响，结果表明两者对齿轮的冲击影响较大。李应刚等[7]用谐波平衡法研究了外部动态激励下单自由度直齿轮副的非线性振动响应，结果表明系统会出现参数共振和幅值跳跃等非线性动力学行为。盛冬平等[8]建立了齿轮-转子-轴承系统的四自由度的弯扭耦合的非线性振动模型，并分析了转速、啮合阻尼、齿侧间隙以及支承间隙等参数对系统分岔特性的影响。宋雪萍等[9]研究了啮合刚度、支撑刚度和阻尼对压缩机齿轮-转子系统稳定性的影响，结果表明，支撑刚度和阻尼的增大会使系统临界转速提高，进而提高系统的稳定性。王三民等[10]建立了齿轮系统的三自由度耦合振动模型，并研究了支撑刚度和阻尼对系统分岔与混沌的影响，结果表明，两者的相互作用会影响系统进入混沌的途径。靳广虎等[11]综合支撑弹性变形等非线性因素建立了正交面齿轮系统的5自由度动力学模型，并研究了间隙和啮合频率变化时系统响应的变化，认为可以通过调整支撑刚度来改变系统的冲击状态。

综上所述，以往关于直齿轮副分岔与混沌的研究主要集中于3自由度模型且多数文献并未考虑摩擦的作用；而支承刚度对齿轮-转子系统的分岔和混沌具有很重要的影响，但过去关于支撑刚度对直齿轮副非线性影响的研究则相对较少或只研究了固定激励频率下支撑刚度对系统分岔、振幅跳跃及混沌的影响。最近的文献[12]虽建立了自由度数量较多的齿轮-转子模型，但模型中并未考虑摩擦的影响且对于支撑刚度对系统分岔特性及冲击状态的影响并未作深入地分析。综合上述情况，本文基于周期扩大法[13]的思想建立了一对直齿轮副的六自由度非线性动力学模型，模型中采用矩形波时变刚度，并考虑了齿面摩擦、齿侧间隙和综合啮合误差等非线性因素，深入研究了支撑刚度对系统的分岔与混沌、动态啮合力及冲击状态的影响，为实际中齿轮转子系统的振动特性分析提供了一定的理论依据。

1　周期扩大法及啮合刚度的处理

直齿轮的重合度ε一般位于1到2之间，这就意味着齿轮在传动时处于单双齿交替啮合状态，如图1(a)所示为一对齿的啮合历程，齿轮的单、双齿区啮合时间分别为t1、T0-t1，其中T0为一个法距对应的啮合时间。周期扩大法的思想即为当一对齿啮出时，假设继续保持啮合一个单齿区啮合时间，但对应的啮合刚度、摩擦因数等参数均为0 ，以一对齿的矩形波时变刚度模型[14-15]为例作说明，假设其扩大周期后的刚度曲线为kh2(t)，则另外一对参与啮合齿的刚度kh1(t)可表示为kh2(t+T0)，轮齿的综合刚度曲线可由两齿对的刚度表示，如图1(b)所示。可知其综合刚度并未因周期的扩大而改变。图中，k1，k2，kmax，kmin分别相关的刚度参数，文中为了进行长期地动力学分析，将单对齿的时变刚度kh2(t)扩展为以2T0为周期的傅里叶级数，则kh1(t)可由kh2(t)得到，两者同取二次谐波项

(1)

式中，a0、a1、a2均为傅里叶展开系数。

(a)　单双齿交替啮合状态

(b)　齿轮的综合刚度曲线图1　齿轮的时变啮合刚度Fig.1 The time varying stiffness of gear pair

2　非线性动力学模型的建立

一对直齿轮副的非线性动力学模型如图2所示。这里引入系统的6个自由度，即{d}={θ1θ2xo1yo1xo2yo2}，图中θ1、θ2为齿轮1、2的扭转角位移；xo1、xo2为齿轮1、2的横向位移；yo1、yo2为齿轮1、2的径向位移。齿轮副的动态啮合力可表示为

图2　直齿轮副非线性动力学模型Fig.2 Nonlinear dynamic model of a spur gear pair

(2)

式中：Fmeshi(i=1,2)为齿对i之间的啮合力；khi(t)(i=1、2)为齿对i之间的时变啮合刚度；chi(i=1,2)为齿对i之间的啮合阻尼；δ(t)为齿轮副的动态传递误差(DTE)，e(t) 为静态传动误差。f(x)为具有分段线性特征的间隙非线性函数

(3)

2.1摩擦力及摩擦力矩

对于一对啮合齿，当啮合点在节圆上部和下部时，由于齿面间的滑动速度改变方向，致使摩擦力的方向发生改变。根据库伦摩擦定律，由式(1)可得到啮合时各齿对之间的齿面摩擦力

fi=μiλiFmeshii=1,2

(4)

式中μi为齿面摩擦因数，其大小随齿对的相对滑动速度的变化而周期性变化，但变化范围不大；λi为扩大周期后的摩擦力方向系数。

(5)

摩擦力矩可由几何关系推导得到，S1i，S2i(i=1,2)表示齿对i之间的摩擦力对齿轮1、齿轮2的力矩，rbi、rai分别为齿根圆、齿顶圆半径；α为压力角，w1为主动轮角速度，Pb为基圆节距。

(6)

2.2动力学方程及量纲一化

可得图2模型中齿轮副的非线性动力学微分方程

(7)

引入以下无量纲参数，对式(7)进行无量纲处理

F=T1/rb1me1+T2/rb2me2

τ=wnt,δ(t)=ubn,xo1=x1bn,

yo1=y1bn,xo2=x2bn

yo2=y2bn,ch1=ch2=ch,cn=ch/2Mewn

c3=c2x/ch,c4=c2y/ch,k1=k1x/k0,k2=k1y

/k0,k3=k2x/k0,k4=k2y/k0,w=wh/wn,

用t替代τ，则微分方程为

式中：f1、f3为轴承的横向预紧力，f2、f4为轴承的径向预紧力；ζ1(t)、ζ2(t)均为周期函数；ρ1(t)、ρ2(t)为摩擦力方向系数的函数。

同样，为了进行长期的动力学分析，对ζ1(t)，ζ2(t)，ρ1(t)、ρ2(t)展开成以2T0为周期的傅里叶级数，类似于式(3)对函数的傅里叶级数取二次谐波项进行动力学分析。另外，可推导得到量纲一化后的动态啮合力为

3　数值求解及分析

式(8)表示一强非线性时变参数系统，本文采用4～5阶变步长龙格-库塔法对其进行数值求解，为了消去瞬态响应，舍弃前2 000周期的结果。以稳态响应为基础，分别得到系统的poincaré截面图、FFT频谱、分岔图、最大Lyapunov指数等，以此分析支撑刚度对系统分岔特性、啮合状态的影响，系统的主要参数如表1所示。

表1　系统的主要参数

3.1支撑刚度对系统分岔特性的影响

为了方便分析，这里引入支撑刚度和轮齿平均啮合刚度的比值来表征支撑刚度的变化，即式(10)中的ki(i=1,2,3,4)。设置参数Fm=0.1，ej=0.25，cn=0.02，ci=2(i=1,2,3,4)，b=0.4，通过调节ki来研究系统的变化规律。

图3分别为ki=1.3时系统随量纲一频率w变化时的分岔图和最大Lyapunov指数曲线(LLE曲线)。跳跃现象多发生于间隙机构，由图3分岔图可知，在低频区，系统响应在频率w为0.38和0.83时出现了跳跃，对应的LLE曲线出现了指数突变，并且在第二次跳跃之后在w为0.98附近经拟周期途径经环面破裂进入第一个混沌区域 (0.98 1.42)；随后，在频率1.42处经拟周期通道由混沌进入短周期运动。在频率区间 (1.42 1.73)内，系统响应进行了短周期与短周期运动之间的分岔，如分岔图细节图所示；在频率为1.73和2.16处分别经拟周期通道进入和离开第二个混沌区域，总体上，当激励频率w变化时，系统主要经拟周期通道进入混沌运动，对应的LLE指数在此过程经历了“负-零-正”的变化，如图3(b)所示。系统在拟周期分岔点w为0.98、1.42、1.73和2.16处的LLE指数分别为-0.000 114、-0.000 307、0.000 010 8和-0.000 143，由于存在计算精度的问题及量级的对比，这些拟周期点的LLE指数近似为0；另外，对比两图可发现相应的倍周期以及拟周期分岔点处的LLE指数接近于0，且在混沌区域存在一定的周期窗口。

随着ki的增加，当ki=1.75时，系统在w为0.41、0.43、0.48、0.84和0.96处发生了短周期与短周期运动之间的跳变，如图4所示。并且系统在w为1.12、1.34、1.405、1.58、2.02和2.19通过拟周期通道进入或离开混沌，在LLE曲线可看到，在这些分岔点附近，指数也出现了“负-零-正”的变化。结合LLE曲线图可大致确定系统的混沌响应区间为(1.12 1.34)∪(1.405 1.58)∪(1.73 1.825)∪(2.02 2.19)。另外，从分岔图中可见，当系统响应在进入或离开混沌区域(1.73 1.825)时具有“激变”特征，在此区域(图中标示区域)，系统运动经历了“周期2-混沌-周期2-混沌-周期2”的过程，属于通向混沌道路里的“阵发性混沌道路”，对应的LLE曲线经历了“负-正-负-正-负”的过程，曲线的变化趋势比较剧烈，这并不同于通向混沌的拟周期道路。同样，在混沌区域可观察到小范围周期性窗口的存在，对应的LLE指数为负值。

当ki增加至1.98时，如图5分岔图所示，系统响应在w为0.44、0.48、0.51、0.905、0.995和1.045处发生跳变，从LLE曲线中也可明显看到跳变点的存在；系统在频率为1.35、1.57、1.67经拟周期通道进入或离开混沌区；同样由LLE曲线可确定系统的主要混沌区为(1.225 1.35)∪(1.43 1.46)∪(1.57 1.67)∪(1.9 1.99)；从分岔图可看到，系统响应在进入和离开混沌区(1.43 1.46)和(1.9 1.99)时也具有“激变”特征，对应的LLE指数会发生“正-负”或“负-正”的突变，如图中标注区域所示。另外，在频率2.15～2.24之间，系统响应由“周期2-拟周期-周期2”的变化，相应的LLE指数如图所示经历了“负-零-负”的变化。

综上，对比各刚度下的分岔图和LLE曲线图可发现，刚度的提高使得系统响应在低频时的跳跃点增加，并且跳跃点对应的频率值略有增大。另外，系统的混沌区域有所减小，在有些频率区间内混沌逐步退化为周期或拟周期运动，以至于系统的分岔变得更为复杂，同时系统进入混沌的临界频率值相应增大，也从侧面说明了支撑刚度对系统固有频率的影响；再者，随着刚度的增加，系统通向混沌的道路也多样化，出现了激变性和阵发性的混沌道路；对比各LLE曲线可见，随着支撑刚度的增大，混沌区的LLE指数相对减小，说明支撑刚度的增加使系统的混沌吸引子逐步减弱。

(a)分岔图(a)分岔图(a)分岔图

(b)最大Lyapunov指数曲线图3 ki为1.3时随w变化的分岔图和对应的最大Lyapunov指数图Fig.3BifurcationdiagramsandthelargestLyapunovexponents(ki=1.3)(b)最大Lyapunov指数曲线图4 ki为1.75时随w变化的分岔图和对应的最大Lyapunov指数图Fig.4BifurcationdiagramsandthelargestLyapunovexponents(ki=1.75)(b)最大Lyapunov指数曲线图5 ki为1.98时随w变化的分岔图和对应的最大Lyapunov指数图Fig.5BifurcationdiagramsandthelargestLyapunovexponent(ki=1.98)

3.2系统随支撑刚度变化的分岔特性

为了进一步说明支撑刚度对系统的影响，这里主要的参数设置同上节所述，但令w=1，相当于从图3～5所示的分岔图中截取一个w截面，从另外一个角度研究系统响应随刚度比ki的变化。图6所示为系统响应随刚度比ki变化时的分岔图和LLE曲线图。

(a)全局分岔图(b)最大Lyapunov指数曲线(c)局部放大图6 系统随ki变化的分岔图和对应的最大Lyapunov指数图Fig.6BifurcationdiagramsandthelargestLyapunovexponentsofki

图6展示了系统稳态运动随刚度比变化时表现出来的丰富的分岔特性。可以看到，随着刚度比的增加，系统总体经历“混沌-周期”运动的历程，并且运动状态在刚度比ki为1.005、1.053、1.465进行了混沌与周期或拟周期的转变，在1.751、2.557、2.674和3.579处进行了周期运动之间的切换，对应的LLE指数在这些分岔点处也有明显的变化。系统运动的混沌区(设为一、二)主要为(0.65 1.005)∪(1.053 1.465)，图6(c)左图为系统响应在混沌区一、二之间切换的细节分岔图，系统响应经历了“混沌-周期6-混沌”，但状态的切换具有“激变”特征，对应的LLE指数变化也具有突变性，如图b标注区域所示。相应地，图7为系统运动在此区间内切换时的poincaré截面图。

随着ki的提高，系统在ki为1.464 7附近离开混沌区，但从分岔图中并不能直接判断分岔类型。由图9所示poincaré截面的变化可判断，当ki从1.464 7到1.464 2变化时，系统由周期5运动经次谐分岔进入拟周期1运动，然后经锁相，再由不稳定的吸引子后进入混沌运动，此属于非常规的混沌道路，对应的poincaré截面经历了“五个离散的点(e)-封闭的自缠绕圆环(d)-非封闭的圆环吸引子(对应系统在环面上的锁相运动,图(c))-不稳定的吸引子(环面破裂，图(b)-混沌(a)”的变化。相应的LLE指数经历了“负-零-负(接近于0)-正”的变化。

当系统离开混沌区后，由局部分岔图6(c)可知，当ki∈(1.464 7 1.764)时，系统在1.551时由周期5运动经倍周期分岔进入周期10运动，随后经历了复杂的“周期10-周期1-周期10-周期1-周期5-周期1”的变换，分岔类型均为次谐分岔，对应的LLE指数也发生了“突变”。当ki∈(1.764 4.112)时,系统运动在ki为2.336时经倍周期分岔进入周期2运动，随后由经多次“跳跃性”的倍周期分岔和倒分岔进入稳定的周期1运动。ki=2.336处的LLE指数为-1.82×10-5，而在跳跃性倍周期分岔点处的LLE指数同样产生了“跳变”。

(a) ki=1.001(b) ki=1.005

(c) ki=1.049(d) ki=1.053图7 混沌区一、二切换时的poincaré截面变化Fig.7ThechangesofpoincarémapsfromchaoticregionItoⅡ

(a) ki=1.4642(b) ki=1.46431(c) ki=1.46438

(d) ki=1.46453(e) ki=1.4647图8 ki在1.4642～1.4647时系统poincaré截面图和FFT谱Fig.8PoincarémapsandFFTspectrumsofsystemviaki∈[1.46421.4647]

综上可知，支撑刚度对系统分岔特性的影响不容忽视，随着支撑刚度的变化，系统表现出丰富的非线性动力学行为，支撑刚度的提高能使系统由混沌逐步趋向稳定的周期运动，但过程中出现了较多的跳跃性分岔点，而分岔点对应的是系统状态的“突跳”，会造成系统的运动稳定性能低下，因此在设计时支撑刚度时应尽量避开相应的分岔点。

3.3支撑刚度对啮合状态的影响

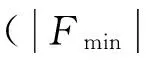
图9　不同刚度比下DMF随w变化的最大值和最小值曲线Fig.9 Maximum and Minimum curve of DMF with different ki

图10　DMF随刚度比变化的最大值和最小值曲线Fig.10 Maximum curve and Minimum curve of DMF via ki

4　结　论

(1) 在低频(激励频率)区，系统经多次跳跃由拟周期通道进入混沌运动，随着支撑刚度的提高，系统的跳跃点数目增加，且跳跃点对应的频率值逐渐增大。

(2) 当支撑刚度增大时，系统的混沌区域有所减小且混沌的程度有所降低，且在有些频率区间内混沌运动退化为周期或拟周期运动，使得系统的分岔特性变得更为丰富复杂，同时系统进入混沌的临界频率值也随之增大；再者，系统通向混沌的道路也多样化，除了拟周期通道之外，还出现了激变性和阵发性的混沌道路。而在定频率(混沌区的某一频率)条件下，不断地提高支撑刚度，系统由混沌运动经多次分岔(倍周期分岔和次谐分岔)最后稳定在周期运动且过程中出现了激变性混沌道路和“周期5-拟周期-锁相-不稳定吸引子-混沌”的非常规混沌道路。

(3) 当支撑刚度增加时，系统的1/2次谐振有所加强，对应的DMF明显增加；并且，DMF最大值和最小值曲线整体后移，峰值频率区域(也即转速区)减小。同样在定频率条件下，当支撑刚度不断增大时，混沌区的DMF的最大值和最小值的绝对值逐渐减小，而周期区的DMF则变化较小；整体上，当刚度提升时，齿轮啮合状态经历了“双边冲击-单边冲击-无冲击”的历程，因此，适当地提高支撑刚度可对系统的混沌进行抑制进而提高系统的稳定性。

[1] Vaishya M, Singh R. Analysis of periodically varying gear mesh systems with Coulomb friction using Floquet theory[J]. Journal of Sound and Vibration, 2001, 243(3): 525-545.

[2] Li S, Kahraman A. A tribo-dynamic model of a spur gear pair[J]. Journal of Sound & Vibration, 2013, 332 (20):4963-4978.

[3] Wang J, Zheng J, Yang A. An analytical study of bifurcation and chaos in a spur gear pair with sliding friction[J]. Procedia Engineering, 2012, 31(16):563-570.

[4] Moradi H, Salarieh H. Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity[J]. Mechanism & Machine Theory,2012,51(5):14-31.

[5] 张锁怀，李忆平. 用谐波平衡法分析齿轮耦合的转子-轴承系统的动力特性[J]. 机械工程学报，2000，36(7):18-22.

ZHANG Suo-huai，LI Yi-ping. Dynamic analysis of a rotor-bearing system geared by means of the harmonic balance method[J]. Chinese Journal of Mechanical Engineering，2000，36(7): 18-22.

[6] 张义民, 路金昌, 胡鹏. 转速及扭矩对啮合齿轮副非线性特性影响分析[J]. 东北大学学报：自然科学版, 2014, 35(3):397-401.

ZHANG Yi-min, LU Jin-chang, HU Peng.Non-linear characteristics analysis of gear pairs with the impact of rotational speed and torque[J]. Journal of Northeastern University:Natural Science, 2014,35(3):397-401.

[7] 李应刚, 陈天宁, 王小鹏,等. 外部动态激励作用下齿轮系统非线性动力学特性[J]. 西安交通大学学报, 2014, 48(1):101-105.

LI Ying-gang, CHEN Tian-ning, WANG Xiao-peng, et al. Non-linear dynamics of spur gear pair under external periodic excitation[J]. Journal of Xi’an Jiaotong University,2014,48(1):101-105.

[8] 盛冬平, 朱如鹏, 陆凤霞,等. 多间隙弯扭耦合齿轮非线性振动的分岔特性研究[J]. 振动与冲击, 2014, (19):116-122.

SHENG Dong-ping, ZHU Ru-peng, LU Feng-xia, et al. Bifurcation characteristics of bending-torsional coupled gear nonlinear vibration with multi-clearance[J]. Journal of Vibration and Shock, 2014, (19):116-122.

[9] 宋雪萍, 于涛, 李国平, 等. 齿轮轴系弯扭耦合振动特性[J]. 东北大学学报, 2005, 26(10): 990-993.

SONG Xue-ping, YU Tao, LI Guo-ping,et al. Characteristics of bending-torsional coupled vibrations of gear shafting[J]. Journal of Northeastern Uinversity,2005, 26(10), 990-993.

[10] 王三民, 沈允文, 董海军. 多间隙耦合非线性动力系统的分叉与混沌[J]. 西北工业大学学报,2003,21(2):191-194.

WANG San-min, SHEN Yun-wen, DONG Hai-jun. Bifurecation and chaos in a nonlinear dynamic system with multiple clearances and time-varying stiffness[J].Journal of Northwestern Polytechnical University,2003,21(2):191-194.

[11] 靳广虎, 朱如鹏, 鲍和云. 正交面齿轮传动系统的非线性振动特性[J]. 中南大学学报:自然科学版,2010,41(5):1807-1813.

JIN Guang-hu, ZHU Ru-peng, BAO He-yun. Nonlinear dynamical characteristics of face gear transmission system[J]. Journal of Central South University,2010, 41(5): 1807-1813.

[12] 崔亚辉, 刘占生, 叶建槐,等. 内外激励作用下含侧隙的齿轮传动系统的分岔和混沌[J]. 机械工程学报, 2010, 46(11):129-136.

CUI Ya-hui, LIU Zhan-sheng, YE Jian-huai, et al. Bifurcation and chaos of gear transmission system with clearance subjected to internal and external excitation[J]. Chinese Journal of Mechanical Engineering. 2010, 46(11):129-136.

[13] Tang J, Chen S, Zhou C. An improved nonlinear dynamic model of gear transmission[C]//ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference[J]. American Society of Mechanical Engineers, 2007: 577-583.

[14] Gill-Jeong C, Nonlinear behavior analysis of spur gear pairs with a one-way clutch[J]. Journal of Sound and Vibration,2007(301):760-776.

[15] Walha L, Fakhfakh T, Haddar M. Nonlineardynamics of a two-stage gear system with mesh stiffness fluctuation, bearing flexibility and backlash[J].Journal of Mechanism and Machine Theory,2009(44):1058-1069.

Non-linear dynamic features of a gear system with multi-DOF subjected to internal and external excitation

XIANG Ling, JIA Yi, LI Yuan-yuan, FENG Xiao-ran, GAO Xue-yuan, DI Wei-wei

(Mechanical Engineering Department, North China Electric Power University, Baoding 071003, China)

Based on the period-enlargement method, a 6-DOF nonlinear dynamic model of a spur gear pair was developed considering rectangular-wave mesh stiffness, backlash, sliding friction and other no-linear factors. Periodic terms in the dynamic equations were expanded with Fourier series and numerical integration was used to investigate the influences of system parameters including rotating speed and supporting stiffness on the bifurcation features of the system. The Poincaré maps, bifurcation diagrams, FFT spectrum and the largest Lyapunov exponents were achieved to systematically analyze the effects of supporting stiffness on the gear system . It was shown that the system goes into chaos motion after several “frequency hoppings” with increase in exciting frequency; besides, as the supporting stiffness increases, the number of “frequency hoppings” increases accordingly, the regions of exciting frequency corresponding to chaos motion are smaller and delayed, in other words, the system enters later chaotic motion due to the larger supporting stiffness; moreover, the roads to chaos become diverse, in addition to quasi-periodic route, there exist intermittent and catastrophic chaos routes and the non-typical ‘period 5 quasiperiodic-locked-unsteady attractor-chaos’chaos route; with increase in supporting stiffness, the resonance of the system at w/2(w is the exciting frequency) becomes stronger and the dynamic meshing force (DMF) increases accordingly, but the DMF in some chaotic regions decreases gradually, the gear system exhibits a state change of “double-side impact-single-side impact-no impact”.

spur gear pair; nonlinear dynamics; friction; backlash; supporting stiffness

10.13465/j.cnki.jvs.2016.13.025

国家自然科学基金(51475164)；河北省自然科学基金(E2013502226)

2015-05-26修改稿收到日期：2015-07-10

向玲 女，博士,教授，1971年生

TH113

A