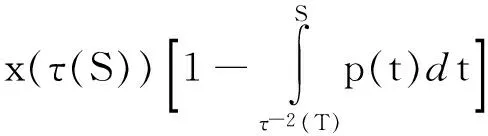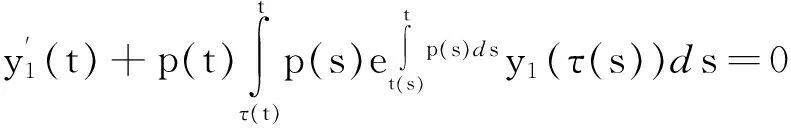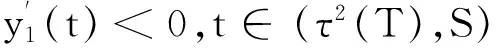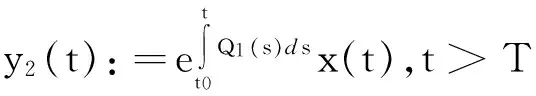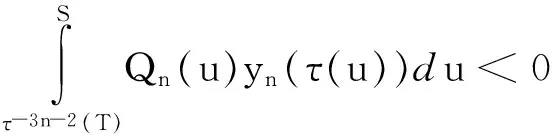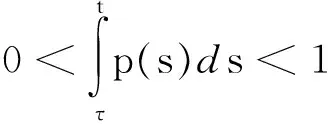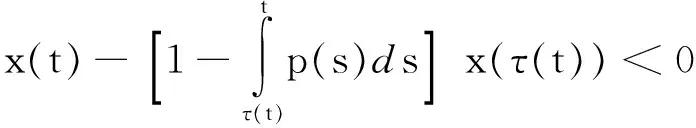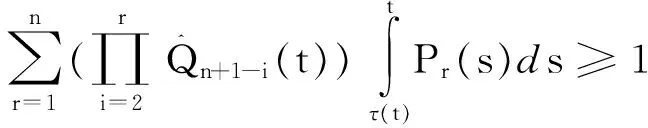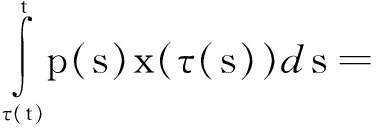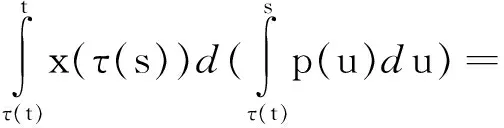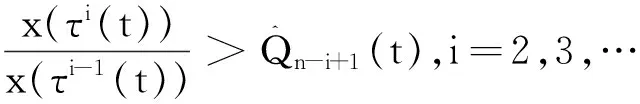一阶变时滞微分方程解的零点间距上界估计

王 淑 萍

(中国石油大学(北京)理学院 数学系，北京 102249)



一阶变时滞微分方程解的零点间距上界估计

王 淑 萍

(中国石油大学(北京)理学院 数学系，北京 102249)

给出了一阶变时滞微分方程的零点存在条件，从而相应地给出该方程解零点震荡的条件以及零点间距的上界估计，给出了关于方程零点分布更广泛的结论.

零点间距；震荡；变时滞

1　引　论

本文给出下述一阶变时滞微分方程的零点存在的判定条件，从而进一步得到该微分方程零解震荡的判定条件以及零点间距的上界估计.

考虑如下变时滞微分方程

x′(t)+p(t)x(τ(t))=0,t≥t0

(1)

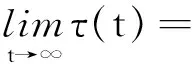
关于时滞微分方程的零解震荡性以及零点间距上界的估计，到目前为止这方面的著述颇丰[1-13]，具体的内容综述，笔者在这里不再赘述.

至于本文所涉及的研究内容，最新的进展可追溯到HassanA·El-Morshedy，FaroqA.Baker，LynnErbe，HongwuWu等诸多文献中，较为开端性的工作可以从B·G·Zhang[2]和YongZhou[4]的文献中读到，El-Morshedy[8]给出了一阶常时滞微分方程的零点分布的诸多性质；之后HongwuWu等[6，9，10]给出了更多的推广以及一些新的结论；可以在文献[11]中看到他们在中立型泛函微分方程零解分布方面的结果，文献[12]的结果对于一阶变时滞微分方程的零点分布作了更进一步的推广，无疑结果是令人兴奋的.本文是对El-Morshedy[8]一些结论的推广，而其中的证明思想正是源于上述的诸多文献.

本文会多处用到τ(t)的逆函数，为了简明陈述文中的结论，引入下面的记号：

τ0(t)=t

τ-i(t)=τ-1(τ-(i-1)(t)),i=1,2,…

我们定义d(x)表示相邻零点间的最大距离.

2　主要结论

定理1：设x(t)是方程在[t0,∞)的解，假设T≥t0，并且S∈(τ-2(T),τ-3(T))，如果

(2)

那么区间(T,S]至少包含x(t)的一个零点，进一步，如果对于所有的t≥t0，

(3)

那么方程存在震荡解x(t).

证明：我们假设对于t∈(T,S)，x(t)≠0 ，S∈(τ-2(T),τ-3(T))，不失一般性，我们不妨设t∈(T,S)，x(t)>0于是

x(τ(t))>0,t∈(τ-1(T),S)，

并且

x′(t)=-p(t)x(τ(t))≤0，t∈(τ-1(T),S).

因此，x(τ(t))在区间(τ-2(T),S)上非增，于是我们可以得到：

因为 x(τ-2(T))≤x(τ(S))，

因此0

推论1：设x(t)是方程在[t0,∞)的解，假设t≥t0，并且St∈(τ-2(t),τ-3(t)]，如果

(4)

那么d(x)≤supt≥t0(St-t).

注：如果我们令τ(t)=t-τ，上述结论便简化为文献[8]中的结果，显然上述结论是对文献[8]中定理2.2给出结论的推广.在推论1中，如果我们用τ-n(t)代替其中的t可得到下述结论

推论2：设x(t)是方程在[t0,∞)的解，假设t≥t0，并且St∈(τ-n-2(t),τ-n-3(t)]，如果

(5)

那么d(x)≤supt≥t0(St-τ-n(t)).

下面定义序列{Qn(t)}满足

Q0(t)=p(t),t≥T

定理2：设n为一正整数并且有下式成立

(6)

那么方程在(T,S)上有零解.进一步，对于任意，如果

(7)

那么方程存在震荡解，且零点间的距离为

d(x)supT≥t0(St-t),St∈(τ-3n-2(t),τ-3n-3(t)).

证明：不失一般性，对于T≥t0不妨设在(T,S)上x(t)>0为方程的任一解，S∈(τ-3n-2(T),τ-3n-3(T))，于是我们得到：

容易看出

t∈(τ-2(T),S).

于是

迭代n次后我们得到

yn(S)-yn(τ-3n-2(T))+

S∈(τ-3n-2(T),τ-3n-3(T))

进而得到

yn(S)-yn(τ-3n-2(T))+

-yn(τ-3n-2(T))≥-y(τ(S))

于是

由yn(S)>0知上式不成立，从而推断出区间(T,S)上至少有x(t)的一个零点.相应地，我们可以得到解的震荡性以及零点间距的上界.

设x(t)是方程(1)在[t0,∞)上的解并且在区间[T0,T]上大于0，这里T0≥t0,T≥τ-3(T0)，并且我们假设

(8)

我们容易知道x′(t)<0,t∈[τ-1(T0),T].因此，当t>τ-3(T0)时，x(τ(s))在区间[τ(t),t]上递减，且有

从而有

进一步，当t≥τ-4(T0)时，我们有

我们看到式(1)满足

两边积分可得到

从而得到

通过归纳法可证明：

(9)

接下来我们定义序列{Pn(s)},s∈(τ(t),t)如下

定理3：设有正整数n满足

(10)

那么方程(1)有震荡解，且d(x)≤supT0≥t0(τ-n-2(T0)-T0).

证明：假设x(t)>0，t∈[T0,T]且T>τ-n-2(T0),T0≥t0.首先，我们容易得到下式

利用归纳法可知

另一方面，由式(9)知

于是

从而得到

于是有

x(t)-[1-

(11)

对于所有的t∈[τ-n-2(T0),T]，式(11)与我们给出的假设矛盾，结论成立.

[1]ERBELH,KONGQ,ZHANGBG.Oscillationtheoryforfunctionaldifferentialequations[M].NewYork:MarcelDekker, 1995.

[2]ZHANGBG,ZHOUY.Thedistributionofzerosofsolutionsofdifferentialequationswithavariabledelay[J].J.Math.Anal.Appl., 2001, 256: 216-228.

[3]LIANGFX.Thedistributionofzerosofsolutionoffirstorderdelaydifferentialequations[J].J.Math.Anal.Appl., 1994, 186: 383-392.

[4]ZHOUY.Thedistributionofzerosofsolutionsofneutraldifferentialequations[J].HiroshimaMath.J., 1999, 29: 361-370.

[5]YEH,GAOG.TheDistributionofzerosofsolutionsofneutraladvanceddifferentialequations[J].AppliedMathematicsLetters, 2004, 17: 997-1005.

[6]WUHW,XUYT.Thedistributionofzerosofsolutionsofneutraldifferentialequations[J].AppliedMathematicsandComputation, 2004, 156: 665-677.

[7]SHANW,NIUZ,GUOY.Thedistributionofzerosofsolutionsforaclassofneutraldelaydifferentialequations[J].AppliedMathematicsandComputation, 2007, 186: 1137-1150.

[8]HASSANA，El-MORSHEDY.Onthedistributionofzerosofsolutionsoffirstorderdelaydifferentialequations[J].NonlinearAnalysis, 2011, 74: 3353-3362.

[9]WUH,CHENGSS.Upperboundsforthedistancesbetweenadjacentzerosofsolutionsofdelaydifferentialequations[J].AppliedMathematicsandComputation, 2011, 218: 3379-3386.

[10]WUHW,ERBEL.Onthedistancebetweenconsecutivezerosofsolutionsoffirstorderdelaydifferentialequations[J].AppliedMathematicsandComputation, 2013, 219: 8622-8631.

[11]BAKERFA,EL-MORSHEDYHA.Thedistributionofzerosofallsolutionsoffirstorderneutraldifferentialequations[J].AppliedMathematicsandComputation, 2015, 259: 777-789.

[12]WUH,ERBEL,PETERSONA.Upperboundsforthedistancesbetweenconsecutivezerosofsolutionsoffirstorderdelaydifferentialequations[J].J.Math.Anal.Appl., 2015,AcceptedManuscript.

[13]STAVROULAKISIP.Asurveyontheoscillationofdifferentialequationswithseveraldeviatingarguments[J].JournalofInequalitiesandApplications, 2014, 2014: 399.

Upper bounds estimation of distances between consecutivezerosoffirstorderdifferentialequationwithvariabledelay

WANGShu-ping

(China University of Petroleum (Beijing), Science Department of Mathematics, Beijing 102249，China)

Inthispaper,aconclusionfortheexistenceofzerosoffirstorderdifferentialequationwithavariabledelaywasgiven,provedatheoremontheoscillationofzerosofsuchequationsandanestimationofdistancebetweenconsecutivezeroswillbeproved.Ageneralconclusiononthedistributionofzerosofsuchequationswasgiven.

distancebetweenconsecutivezeros;oscillation;variabledelay

2015-09-09.

国家自然科学基金(11071257)；中石油创新基金项目(2011D-5006-0307)

王淑萍(1989-)，女，硕士，研究方向：微分方程与动力系统.

O175

A

1672-0946(2016)04-0473-03