高数思想指导　完善初数错漏

彭翕成

高数思想指导完善初数错漏

彭翕成

有老师表示，高等数学对中学数学的指导作用毋庸置疑，很多题目用初等数学方法解答较为困难，但使用高等数学方法则比较简单。比如罗必塔法则、泰勒展开式，让很多题目变得容易，因为命题人很可能就是从高等数学里获得灵感。问题是，考试时不能直接应用这些高等数学公式，可谓“空有屠龙技艺，没有用武之地”！

这种情况确实存在。这就好比成年人做小学的应用题，本来用列方程很容易解决，但限于算术方法，解答起来则十分困难。这说明高等数学应用于初等数学，需要研究如何化用，而不能照搬。除了明面上的应用，也可以是无形中的渗透，指导我们从更高的角度认识问题，特别是在初等数学中容易忽视的问题。下面笔者举例说明。

多本资料上有这道题，解法也各不相同。

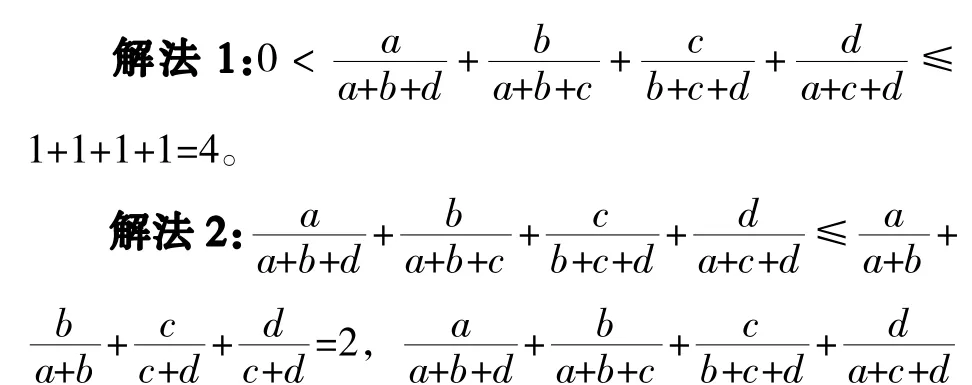
由于a，b，c，d是任意正实数，放缩时等号不能取到，所以1＜s＜2。

对比之下，相信大多数人都会选择解法2。但解法2真的就是完美的么？要知道此题是第16届IMO试题，又怎会如此容易！

解法2只是证明了1＜s＜2，但s能否真的取尽（1，2）中的所有数？如果不能证明s取尽（1，2）中的所有数，那只是说明了1（2）是s的下（上）界，而不能说明是下（上）确界，也就和解法1中得到范围（0，4］并无实质的区别。

（1，2）中的所有数。

思考：解法1并无错，只是得到（0，4］是下（上）界，而非下（上）确界，需要进一步压缩。解法2利用放缩技巧，得到更精确的取值范围，只是忽视了连续性。中学里接触的函数几乎都是初等函数，多数情况下不会出问题，因而这一问题也常常被忽视。而对学过高等数学的老师而言，还是要做到心中有数为好。

这样解答看似没有问题，但对学习过高等解析几何的人来说，遇到此题应该很快地联想到这是一个平面和单位球，而原点到平面的距离要大于球的半径1，平面与球不相交，意味着方程组无实数解。当Y=0时，则是中学里比较熟悉的二维版本这里的直线和圆也是不相交的。从无实数解可知无实数解，这与题目中x，y，z是 3个实数矛盾，此题为错题。

由于中学里并不讲点到平面的距离公式（其实可看作是点到直线距离公式的升级版本，类比提一下也无妨），所以发现问题之后，需要另找途径来说明。

利用不等式3（X2+Y2+Z2）≥（X+Y+Z）2，即3×1≥22，矛盾。该不等式的推导可用恒等式：3（X2+Y2+Z2）= （X+Y+Z）2+（X-Y）2+（Y-Z）2+（Z-X）2，这样初中生也就能理解了。

不只一次看到这样的解法。如果中学生这样解，倒还可以理解。作为学过线性代数的中学老师，出现这样的解法很是不应该。

在线性代数中，求解线性方程组Ax=B的解的数量有三种情况：无解、唯一解、无穷多解。对于有无穷多组解的方程组，解方程组的本质就是用一组可以自由取值的变量（称为自由变量）表示其余变量（称为主变量）。对自由变量的任一组值，都能唯一确定主变量的值，它们一起构成方程组的一个解。需要特别强调，主变量和自由变量的分法并不唯一。

单纯从解题而言，这样的代换解法并不好。可利用例2的不等式3（X2+Y2+Z2）≥（X+Y+Z）2来证，或是由展开，或使用均值不等式

例4若ax+by=1，bx+cy=1，cx+ay=1，ac-b2≠0，求证：ab+bc+ca=a2+b2+c2。

所以ab+bc+ca=a2+b2+c2。

看到上述题目和解答，第一感觉就是条件ac-b2 ≠0多余。因为上述证明稍加改写就可去掉这个条件。

证法1（改写）：由ax+by=1，bx+cy=1，得acx+bcy= c，b2x+bcy=b。

相减，得（b2-ac）x=b-c。

同理，得（b2-ac）y=b-a。

代入cx+ay=1，得（b2-ac）cx+a（b2-ac）y=b2-ac，得c（b-c）+a（b-a）=b2-ac。

所以ab+bc+ca=a2+b2+c2。

这样一来，b2-ac不出现在分母，不管其是否为0都不受影响。至于将cx+ay=1两边同乘b2-ac，也无需考虑b2-ac是否为0。

证法2（武汉陈起航提供）ab+bc+ca=ab（ax+by）+ bc（bx+cy）+ca（cx+ay）=a（2bx+cy）+b（2cx+ay）+c（2ax+ by）=a2+b2+c2。

证法3：ab+bc+ca-a2-b2-c2=

，而不是（b2-ac）x=b-c。

进一步想，就会发现，条件ac-b2≠0纯属画蛇添足。因为所求等式ab+bc+ca=a2+b2+c2可转化为（a-b）2+（b-c）2+（c-a）2=0，等价于a=b=c，可推出acb2=0。这意味着条件ac-b2≠0不仅多余，还造成了矛盾。添上脚的蛇也就不再是蛇，添上矛盾条件的题也就不再是合格的题了。

后面三种证法表明，无需考虑b2-ac是否为0。题目中加上ac-b2≠0这一条件，可能是命题者为了降低难度，考虑到中学生更习惯

证法2：（9x3-17x2+9）′=27x2-34x=0，可得x=0或分析函数增减性可知，当时，9x3-17x2+9取得最小值

这样做，让学习者一方面是无比崇拜，另一方面则是望而生畏。这让人想起关于数学家高斯的一段评语：“高斯并不喜欢教书，而且通常给人的感觉是冷冷的，故和其他数学家相处得不好，或许是因为他无时无刻都在思考研究，因而疏于人际关系吧！终其一生，高斯总是静静地将答案写下，不留一点计算痕迹，而且对答案有绝对的把握，就像雪地中狐狸总是用尾巴扫拭足迹一般。”

变式教学是数学教学中的常用招数。老师在讲完一道题目之后，常常会给出一些变式，既巩固原题，又开阔视野。有时不直接给出变式，而是启发学生，你能从这个问题想到什么，能否提出新问题。这样的启发自然是好的。但有时也容易出问题，哪怕是看似简单的变化。

比如，学完勾股定理之后，有些老师会补充：凡满足x2+y2=z2的整数解称之为勾股数，如何求解勾股数呢？讲解完勾股数的求法之后，如果学生再问，如何求解x3+y3=z3，x4+y4=z4，…，xn+yn=zn，这可就麻烦了。

证法1：

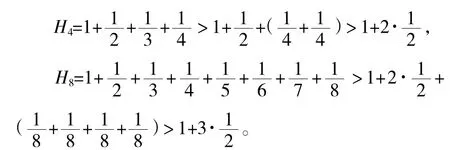
相当多的微积分教材都是采用这种证明，称之为经典并不为过。但经典的是不是最好，是不是就没有商榷、改进的余地呢？并非如此。

中学没有无界这个概念，但通过分析，学生可以看到这个结果是要多大就有多大的。

这是QQ群里网友求助的问题。问题一出，热心网友纷纷支招，提供各种解题思路。

求助者问：思路很多，谁最终解出来了么？结果没一人给出解答。

我说：这题是你自己改编的吧，原题是什么？

他不承认，说：哪有什么原题，这明明是一个独立完整的题目，数列的每一项都是唯一被确定的。

我说：那我搞不定。大胆说一句，没人搞得定。

他说：你做不出来，怎么能确定其他人也做不出来？

他说：你讲的好玄乎，能讲清楚一点吗？

我问：你知道虫口模型吗？

他说：不知道。

我说：虫口模型也是二次函数迭代，异常复杂。你不知道其厉害，所以无所畏惧。用最基本的思路来思考，当一时找不到通项公式的时候，常常会算出数列的前几项，希望从中找出规律，有助于解题。

数列的前几项是：

这时，他才老实交代，其实是在做：数列满足a0=，对于自然数n，，则的整数部分是______。

他希望求出an，代入求解。他将求an当作是计算的整数部分的必要条件，事实上并非如此。求解整数部分，是一个近似值，远比求解an的通项公式简单。解法如下：

因为an递增，于是，显然，从而，所以整数部分为3。

以上案例说明，如果研究者了解一些问题的数学背景，教学和教研就可以少走很多的弯路，少犯一些错误，从而更深刻地认识问题，更快速地解决问题。更多案例参看笔者的新书《从初等数学到高等数学》。

（作者单位：华中师范大学国家数字化学习工程技术研究中心）