Leibniz n-代数的Frattini扩张
关宝玲,韩 旸
(齐齐哈尔大学理学院,黑龙江,齐齐哈尔 161006)
Leibnizn-代数的Frattini扩张
关宝玲,韩旸
(齐齐哈尔大学理学院,黑龙江,齐齐哈尔 161006)
通过将李代数的Frattini扩张推广到Leibnizn-李代数,得到了Leibnizn-代数的Frattini扩张的一些重要性质,给出了Leibnizn-代数的Frattini扩张的几个充分必要条件.
Leibnizn-代数;Frattini扩张;Frattini理想
作为李代数的推广,Filippov在1985年提出了n-李代数的概念,并给出了n+1维n-李代数的分类.[1]近年来n-李代数得到了丰富的结果.[2-4]同时,人们将n-李代数推广到Leibnizn-代数.[5-6]
在群理论中,Frattini研究了所有极大子群的交集,现称其为Frattini群,并于1885年提出了Frattini子群的概念.1967年,Frattini群的理论被引入到李代数中.[7]同时,Stagg对Frattini子代数理论进行了深入研究,引入了李代数的广义Frattini子代数及Frattini理论.[8]21世纪初,Frattini群和广义Frattini群的理论已经完善,一些代数的Frattini理论也得到了广泛研究.[2,9,10-17]本文类比广义Frattini群理论,研究Leibnizn-代数的Frattini扩张.以下总假设L是特征零域F上的有限维Leibnizn-代数.
1 预备知识
定义1[6]若L是域F上具有n元线性运算的向量空间且满足
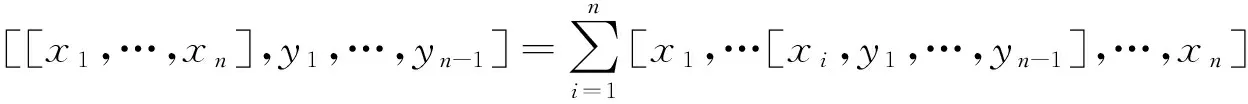
则称L为Leibnizn-代数.
定义2[5]设L是Leibnizn-代数,若L的子空间B对换位运算封闭,即[B,B,…,B]⊆B,则B是L的子代数.若L的子代数I满足[I,L,…,L]⊆I,则称I为L的理想.设I是L的理想,如果[I,I,L,…,L]=0,则称I为L的交换理想.
定义3[6]设L是Leibnizn-代数,M是向量空间.若在M上定义n元运算
[-,…,-]:L⊗i⊗M⊗L⊗n-1-i→M,0≤i≤n-1,
满足(2n-1)个方程,其中这(2n-1)个方程是从下面方程(1)中,分别令(2n-1)个变元x1,…,xn,y1,…,yn-1中的每一个属于M,而其余的都属于L得到,
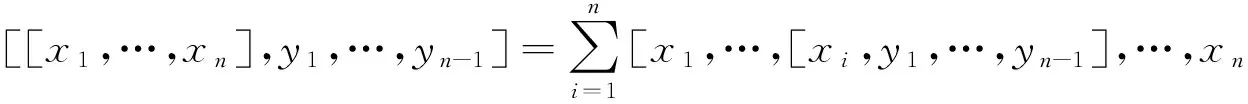
(1)
则称M为Leibnizn-代数L的模.
定义4设L是Leibnizn-代数,L的所有极大子代数的交集称为Frattini子代数,用F(L)表示.包含于F(L)中的L的极大理想称为Frattini理想,用φ(L)表示.
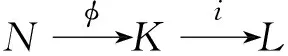
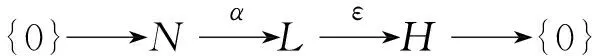
称此为正合列代表扩张(L,ε).若Ker(ε)⊆φ(L),则称扩张(L,ε)是Frattini扩张.
2 Frattini扩张
引理1设(L,ε)是H的扩张,其中Ker(ε)是交换的有限维H-模.若J是L的极大子代数,且Ker(ε)J,则(J,α)是一个扩张,且Ker(α)是Ker(ε)的极大H-子模.
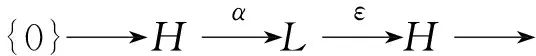
(1) 由于N=Ker(ε)J,且J是L的极大子代数,则J⊆J+N⊆L.由于J是极大的,则J+N=L,注意到(L,ε)是扩张,有L/N≅H,故J+N/N=L/N≅H.又由于J+N/N≅J/J∩N≅H,故J是H通过J∩N的扩张.
(2) 由于N是交换的,且L=J+N,则[J∩N,L,…,L]⊆J∩N,即J∩N是L的理想.
(3) 不妨假设N∩J=0,下面证明N是L的极小理想.设K是L的理想,使得0⊂KN,则
dimJ 故J(J+K).又由于 dimL=dim(J+N)=dimJ+dimN-dim(J∩K)=dimJ+dimN>dimJ+dimK=dim(J+K), 这与J是极大子代数矛盾,故不存在这样的K,即N是极小的,因此N∩J在N中是极大的. 定理1设(L,ε)是H的扩张,且Ker(ε)是交换的.若Ker(ε)是非平凡的不可约H-模,则(L,ε)是Frattini扩张,当且仅当(L,ε)是不可分的. 证明假设 (2) 是不可分扩张的.需要证明N=Ker(ε)是φ(L)的子代数.若Nφ(L),则存在L的极大子代数J,使得NJ,由引理1知(J,α)是扩张,有α=ε|J,Ker(α)是Ker(ε)的最大的H-子模.由于Ker(ε)作为一个H-模是不可约的,则有Ker(α)=J∩N={0},因此α是单射的.又由于(J,α)是扩张,故α是满射,从而α是同构的.因此(1)可分,矛盾. 反过来,假设(L,ε)是广义Frattini扩张,我们需证(1)是不可分的.假设(1)可分,则存在同态φ:H→L,使得εφ=IH,故φ是单同态,H≅Imφ,从而φ:H→Im(φ)是同构的.同样有Im(φ)⊆L,Ker(ε)⊆L.由于扩张可分,则L=Ker(ε)+Im(φ),且Ker(ε)∩Im(φ)={0}.由于Ker(ε)Im(φ),则Im(φ)不是L的极大子代数,因此存在L的极大子代数J使得Im(φ)⊂J⊆L.但又由J的极大性,Ker(ε)⊆φ(L)⊆J,从而Ker(ε)⊆J,且φ(L)⊆J,这与L=Ker(ε)+Im(φ)⊆J矛盾. 定理2设(L,ε)是H的Frattini扩张,则(φ(L),ε)是φ(H)通过Ker(ε)的扩张. 证明由于(L,ε)是H的Frattini扩张,则L/Ker(ε)≅H,故φ(L/Ker(ε))≅φ(H).又由Ker(ε)⊆φ(L),故φ(L/Ker(ε))=φ(L)/Ker(ε). 令L1∶=[L,L,…,L],若L=L1,则称Leibnizn-代数L是完美的. 定理3设L是有限维Leibnizn-代数.若(L,ε)是H通过N的Frattini扩张,H是完美Leibnizn-代数,则L是完美的. 证明假设L不是完美的,且N=Ker(ε),由于(L,ε)是H的Frattini扩张,则有 (L/Ker(ε))=L/N≅H. 由于H是完美的,有(L/H)1≅H1=H,即(L1+N)/N≅(L/N)≅L/N.又由L是有限维的,故L1+N=L.注意到N⊆φ(L)⊆F(L)⊆L1,因此L=N+L1⊆L1⊆L,故L1=L. 定理4若ε:J→M是有限维Leibnizn-代数的满射,L是J的子代数中极小的子代数,且ε(L)=M,则(L,ε|L)是Frattini扩张. 证明设K是L的极大子代数,且假设Ker(ε|L)K,则K⊆K+Ker(ε|L)⊆L.由K的极大性知K+Ker(ε|L)=L.同样有 Ker(ε)◁J,Ker(ε|L)⊆Ker(ε), 且K⊆J,因此 K⊆J⊆K+Ker(ε)⊆J. (3) 设W=K+Ker(ε),则 ε(W)={ε(k+x)|k∈K,x∈Ker(ε)}= {ε(k)+ε(x)|k∈K,x∈Ker(ε)}={ε(k)|k∈K}=ε(K). 由(2)式知ε(L)⊆ε(W)⊆ε(J),即M⊆ε(W)⊆M,因此ε(W)=M,即ε(K)=M,这与L的极小性矛盾.因此Ker(ε|L)包含在L的任意极大理想中,即Ker(ε|L)⊆φ(L).故(L,ε|L)是Frattini扩张. 性质1设(L,ε)是H的Frattini扩张.若α:L→H,β:H→L是同态,且αβ是满射,则β为满射. 证明设K=Im(β)=β(H).由于αβ是满射,则有 α(L)=H=(αβ)(H)=α(β(H))=α(K). 故∀l∈L,∃k∈K,使得α(l)=α(k),则有 α(l)-α(k)=α(l-k)={0}. 引理2设N是L的极小理想.若N在L中是可补的,则N∩φ(L)={0}. 证明若N在L中可补,则对某些HL,L=N+H,且N∩H={0}.由于N◁L,且φ(L)◁L,有N∩φ(L)◁L.由N的极小性,N∩φ(L)={0}或N.若N∩φ(L)=N,则N⊆φ(L),因此N+H⊆φ(L)+H.故L=φ(L)+H,即L=H,矛盾.从而N∩φ(L)={0}. 定理5设L是H通过N的扩张,N是交换的.则L是N的极小Frattini扩张,当且仅当N是L的极小理想且不可补. 证明设N是L的极小理想且不可补.若Nφ(L),则存在L的极大子代数M,使得NM.由于N◁L且M⊆L,则M⊆N+M⊆L.再由M的极大性知N+M=L.由N∩M◁M,N∩M◁N,有N∩M◁N+M=L.而N的极小性表明N∩M={0},矛盾.因此N⊆φ(L),L是N的极小Frattini扩张.反过来,假设N是L的极小理想且是可补的,由引理2知N∩φ(L)=0,因此N不是φ(L)的子代数,从而L不是极小的Frattini扩张.这与已知条件矛盾,故N是L的极小理想且不可补. 定理6Frattini扩张的复合是Frattini扩张. β是满射,且Ker(β)⊆φ(H).需要证明βα是满射,Ker(βα)是满射,且Ker(βα)⊆φ(L). 由于h∈H,α是满射,则存在l∈L,使得α(l)=h.若m∈M,由于β是满射,则存在h∈H,使得β(h)=m.因此 (βα)(l)=β(α(l))=β(H)=m, 故βα是满射. 由α(L)=H,有 α(φ(L))=φ(α(L))=φ(H), 因此φ(L)=α-1(φ(H)).但 Ker(βα)={l|(βα)(l)=0,l∈L}={l|β(α(l))=0,l∈L}= {l|α(l)∈Ker(β),l∈L}={l|l∈α-1(Ker(β))}. 由于Ker(β)⊆φ(H),有 α-1Ker(β)⊆α-1(φ(H))=φ(L). 因此Ker(βα)⊆φ(L). [1]FILIPPOV V T.n-Lie algebras[J].Sib Mat Zh,1985,26(6):126-140. [2]BAI R P,CHEN L Y,MENG D J.The Frattini subalgebra ofn-Lie algebras[J].Acta Math Sin,2007,33:847-856. [3]LIU W L,ZHANG Z X.T*-extension ofn-Lie algebras[J].Linear and Multilinear Algebra,2013,61:527-542. [4]KASYMOV S M.On a theory ofn-Lie algebras[J].Algebra i Logika,1987,26:277-297. [5]CAMACHO L M,CASAS J M,GMEZ J R,et al.On nilpotent Leibnizn-algebras[J].Journal of Algebra and Its Applications,2012,11:265-279. [6]CASAS J M,LODAY J L,PIRASHVILI T.Leibnizn-algebras[J].Forum Math,2002,14:189-207. [7]KAPPE L C,KIRTLAND J.Some analogues of the Frattini subgroup[J].Algebra Collq,1997,4:419-426. [8]MARSHALL E I.The Frattini subalgebra of a Lie algebra[J].J London Math Soc,1967,42:416-422. [9]BARNES D W.The Frattini argument for Lie algebras[J].Math Z,1973,133:277-283. [10]CHEN L Y,MENG D J,ZHANG Y Z.The Frattini subalgebra of restricted Lie superalgebras[J].Acta Math Sin,2006,22:1343-1356. [11]田丽军,关宝玲,王春艳.n-李超代数的Frattini-子代数[J].东北师大学报(自然科学版),2013,45(2):39-42. [12]宋华,王晨迪.李Color代数的极大子代数的基本性质[J].东北师大学报(自然科学版),2012,44(4):26-30. [13]ELDUQUE A.A Frattini theory for malcev algebras[J].Algebras Groups Geome,1984,1:247-266. [14]STAGG K L.Generalizations and analogs of the Frattini subalgebra[D].Raleigh:North Carolina State University,2011. [15]STITZINGER E L.On the Frattini subalgebra of a Lie algebras[J].J London Math Soc,1970,2:429-438. [16]ZHANG Z,CHEN L,LIU W,et al.The Frattini subsystem of a Lie triple system[J].Commun Algebra,2009,37(10):3750-3759. [17]周芳艳,陈良云.n-李代数的广义Frattini子代数及扩张[J].琼州学报,2014(2):1-6. (责任编辑:李亚军) The Frattini extensions of Leibnizn-algebras GUAN Bao-ling,HAN Yang (School of Science,Qiqihar University,Qiqihar 161006,China) The Frattini extensions of Lie algebras are generalized to Leibnizn-algebras.Some important properties of the Frattini extentions for Leibnizn-algebras are obtained.Several necessary and sufficient conditions of the Frattini extensions for Leibnizn-algebras are given. Leibnizn-algebras;Frattini extensions;Frattini ideal 1000-1832(2016)03-0005-04 2015-05-01 黑龙江省自然科学基金资助项目(B2015019). 关宝玲(1974—),女,博士,副教授,主要从事李代数研究;韩旸(1969—),男,博士,副教授,主要从事数据挖掘研究. O 152.5[学科代码]110·21 A [DOI]10.16163/j.cnki.22-1123/n.2016.03.002