Minkowski measure of asymmetry for the convex hull of a triangle and a point

GUO Qi

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

Minkowski measure of asymmetry for the convex hull of a triangle and a point

GUO Qi

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

As one of the most important geometric affine invariants,the measure of asymmetry for convex bodies has recently regained more and more attention of researchers.This paper discussed the Minkowski measure of asymmetry for the convex hull of a triangle and a point in hope to find some particular properties of the Minkowski measures.A precise expression of the Minkowski measure for such convex bodies was given.It shows that the Minkowski measure does have some interesting properties in the case we studied.

convex body；Minkowski measure of asymmetry；convex hull

Document code：AArticle ID：1672－0687（2016）01－0006－05

1　Notation and definitions

As one of the most important geometric invariants,the measure of asymmetry（or symmetry as one prefers）, formulated by Grünbaum in[1]（see also[2]）,for convex bodies（i.e.compact convex sets with non-empty interior in the Euclidean spaces）has recently regained more and more attentions of researchers（see[3-5],[6-10],[11-15]and the references therein）.Many different kinds of measure of asymmetry have been introduced and studied in the history（see,for example,[5],[1],[8],[11],[13]）,among which the Minkowski measure is probably the most important one.

Let Rndenote the n-dimensional Euclidean space.Given a convex body C∈Rn,x∈intC（the interior of C）and a hyperplane H containing x,we have two support hyperplanes H1,H2of C which are parallel to H and lie on either side of H respectively.Let r（H，x）be the ratio,not less than 1,in which H divides the distance between H1and H2,then define rx=sup{r（H，x）|x∈H}.The Minkowski measure of asymmetry（Minkowski measure for brevity）as∞（C）of C is defined by

（notice that a standard compact argument shows that both the superemum and the infimum above are attainable）. A point x satisfying rx=as∞（C）is called an∞-critical point（of C）.For any C there exists at least one∞-critical point（[1-2]）,and for a symmetric convex body,its center is the only critical point.It is known that 1≤as∞（C）≤n for any n-dimensional convex body C,and as∞（C）=1 iff C is symmetric,as∞（C）=n iff C is a simplex（see [2]）.

As known,although the definition is simple,it is very hard in general to calculate the precise value of Minkowski measure for a given convex body.In[6]we gave a formula to calculate the Minkowski measure of theconvex hull of a symmetric body and a point,which reveals some nice properties of convex bodies.In this paper, as a start point of general study,we discuss the Minkowski measure of the convex hull of a triangle and a point. As a result,we provide a formula for computing the Minkowski measure of such convex hulls.

Given a convex body C∈Rnand x∈Rn,we write,where“conv”denotes the convex hull, and then define on Rna function asC（·）by

Clearly,1≤asC（x）≤n for all x∈Rnand asC（x）=as∞（C）for all x∈C.For the precise value of asC（x）for general convex bodies,the only known result was the one shown in[6],where a nice expression of asC（x）is obtained when C is assumed to be centrally symmetric:

Theorem 1[6]For any symmetric convex body C∈Rnwith the origin o as its center,we have

where||·||Cdenotes the norm on Rngenerated by the symmetric convex body C,i.e.the gauge function of C.

In this short paper,we give an expression of asC（x）when C=△is a triangle.We point out that,although the result for triangles seems somehow special,the ideas in the argument might be applied to study general non-symmetric bodies.

2　Main result and its proof

For non-symmetric convex bodies，as is to be expected，the function asC(x)becomes more complicated and more interesting, however we will leave this general topic to other papers.Here we study only the function as△（·）of the triangles△⊂R2through an elegant application of Theorem 1.

Sinceanytwotrianglesareaffinelyeauivalentand asTC（T（x））＝asC（x）for any invertible affine map T:Rn→Rnand x∈Rn,we need only to study the triangle△:=conv{e1,e2,e3}⊂R2,where e1=（0,1）,e2=（－1,0）,e3=（0,－1）∈R2.And set e0＝－e2（see Fig.1）.

Fig.1conv{x，△}for x in I1

Clearly as△（x）＝2 for all x in the closed shadowed areas sinceis still a triangle in such cases.

For other x,by symmetry,we need only to consider the areas I1，I2，I31and I32,where

Denote by||·||Cthe norm generated by C:=conv{e0，e1，e2，e3}，by f1，f2the linear functionals which satisfy f1（e0）= f1（e1）=1 and f2（e1）=f2（e2）=1 respectively.

For x∈I1,by the key observation that,we have by Theorem 1

Remark 110From（1）it follows that if x,y∈I1and f1（x）=f1（y）（i.e||x||C=||y||C）,then as△（x）=as△（y）.

20By Theorem 1,the critical point

For x∈I2,by the key observation,where（see Fig.2）which is a symmetric body with the origin as its center,we have

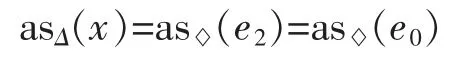
Fig.2conv{x，△}for x in I2

where the last equality follows from Theorem 1 and the fact that

Notice that for x∈I2，there is a unique linear functional f with||f||C′=1,where||·||C′stands for the dual norm of||·||C,such that f（x）=f（e3）and f（e0）=1,soand by Theorem 1

Remark 210From（2）we know that if x,y∈I2with f（x）=f（y）=f（e3）for some linear functional f with ||f||C′=1,then as△（x）=as△（y）（see Fig.2）.

20Similarly,by Theorem 1,for x∈I2,the∞-critical point x*oflocates between in[e2,o], preciselywhere f（with||f||C′=1）satisfies that f（x）=f（e3）and f（e0）=1.From this we see a interesting fact that if x，y∈I2such that f（x）=f（y）=f（e3）for some f with unit norm,then the∞-critical points ofcoincide.

30By（1）（2）,we see that if x1∈I1and x2∈I2such that f（x2）=f（e3）=f1-1（x1）（=||x1||C-1）,where f,f1,C are the same as above,then

In particular as△（μ-1e0）=as△（μe0）for 0<μ<∞.

For x∈I31,there is a linear functional g with||g||C′=1 such that g（x）=g（e1）=1.Let x′be the intersection point of{y|f2（y）= f2（x）}and{y|g（y）=g（e2）},then setwhich is a symmetric convex body with its center at the intersection point x0of the segments[e2,x]and[e1,x′]（see Fig.3）.

Fig.3conv{x，△}for x in I31

Again,by the key observation that,we obtain by Theorem 1

Notice that if x∈I31,then x′∈△,so

Hence we have

Remark 310By（3）we see that if x,y∈I31with f2（x）=f2（y）,then as△（x）=as△（y）（see Fig.3）.

20The∞-critical point x*offor x∈I31,locates between in[e3，x0],concretelywhere.So if x,y∈I31such that f2（x）=f2（y）,then,since f2（x0）= f2（y0）=（1/2）（1+f2（x））,the∞-critical points x*,y*are on the same linewhich is parallel to{f2=1}.

Finally for x∈I32,let g,x′andbe the same as above.Noticing x′∈-△,we have

Remark 410It is clear that g1=g2if g1（e1）=g2（e1）=1 and g1（e2）=g2（e2）.Hence,（4）implies that if x,y∈I32satisfying g（x）=g（y）=g（e1）=1 for some g with||g||C′=1,then as△（x）=as△（y）.

20A similar discuss as above gives thatwhere x0is also the center of,and that if x,y∈I32with g（x）=g（y）=g（e1）=1,then the∞-critical points x*and y*ofare on the same linewhich is clearly parallel to{g=1}.

Fig.4level sets of as（·）

To give the precise expression of as△（x）,we look at the level-sets of as△（x）first,which is interesting in its own right.By symmetry,we may consider only the parts of level-sets restricted to I1∪I2∪I31∪I32.

Let x1，x2，x3，x4，x5be as described in the following Fig.4,then by Remark 1,2,3,4,we have

for all x∈[x1，x2]∪[x2，x3]∪[x3，x4]∪[x4，x5].

Now it is the time to state our main result.

Theorem 2

Proof.By as△（（s，t））=as△（s，-t）,we will argue only for x∈I1∪I2∪I31∪I32.

For x=（s，t）∈[x4，x5]⊂I1,it is easy to know that x5=（s+t，0）（in particular,if x4=（s4，t4）,then x5=（s4+t4，0）.So by Theorem 1,since||x5||=s+t

If x=（s，t）∈[x3，x4]⊂I32,then,hence by Theorem 1

If x=（s，t）∈[x1，x2]⊂I2,then（in particular,if x2=（s2，t2）,then）.Therefore，since as△（μe0）=as△（μ-1e0）for all μ>0,we get

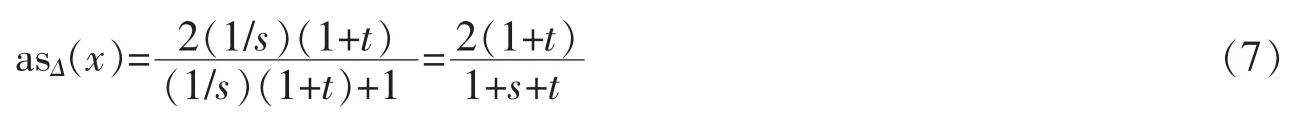
Finally if x=（s，t）∈[x2，x3]⊂I31,then x2＝（（1/2）（1+s－t），（1/2）（1-s+t））.By Theorem 1 again,we have

The proof is completed by the observations that（5）,（7）reduce to，x=（s，t）∈Ii，i＝ 1，2 and that（6）,（8）reduce to，x=（s，t）∈I3i，i＝1，2.□

Remark 5By Theorem 2,it is easy to check that as△（x）→2（the Minkowski measure of asymmetry of triangles）as x→∞in,which,together with the fact that as△（x）=2 for all x in the shadowed areas, shows a somehow strange phenomenon that the convex bodylooks always like a triangle whenever x is far away from the origin.This phenomenon has been found in[6]forwith C symmetric.

Final Remark10As pointed in the beginning,the key idea in our arguments is to find a“suitable”symmetric bodysuch thatfor some x′.So,we have naturally the following question:

How to construct（or which is）the“suitable”symmetric convex body for a given non-symmetric convex body?

20It is shown in[6]that if C is symmetric,then each proper level-set of asC（·）is a homothetic copy of C. This is no long true for non-symmetric ones as seen in Fig.4.However,we see that,for a triangle△,the level-sets of as△still“imitate”-△in a way,especially when the level tends to 1（see Fig.4）.The related questions are:

How to describe such a kind of imitation?

Does such a kind of imitation still hold for general non-symmetric bodies?

[1]GRÜNBAUM B.Measures of symmetry for convex sets[J].Proc Sympos Pure Math，1963，7：233-270.

[2]KLEE V L.The critical set of a convex body[J].Amer J Math，1953，75（1）：178-188.

[3]GLUSKIN E D，LITVAK A E.Asymmetry of convex polytopes and vertex index of symmetric bodies[J].Discrete&Comput Geom，2008，40（4）：528-536.

[4]GROEMER H.Stability theorems for two measures of symmetry[J].Discrete Comput Geom，2000，24（1）：301-311.

[5]GROEMER H，WALLEN L J.A measure of symmetry for domains of constant width[J].Beiträge Algebra Geom，2001，428（2）：517-521.

[6]GUO Q，KAIJSER S.On asymmetry of some convex bodies[J].Discrete Comput Geom，2002，27（1）：239-247.

[7]GUO Q.Stability of the Minkowski measure of asymmetry for convex bodies[J].Discrete Comput Geom，2005，34（1）：351-362.

[8]GUO Q.On p-measure of asymmetry for convex bodies[J].Adv Geom，2012，12：287-301.

[9]GUO Q.GUO J F，SU X L.The measures of asymmetry for coproducts of convex bodies[J].Pacific J Math，2015，276：401-418.

[10]JIN H，GUO Q.Asymmetry of convex bodies of constant width[J].Discrete Comput Geom，2012，47（2）：415-423.

[11]SCHNEIDER R.Stability for some extremal properties of the simplex[J].J Geom，2009，96：135-148.

[12]TOTH G.On the shape of the moduli of spherical minimal immersions[J].Trans of Amer Math Soc，2006，358：2425-2446.

[13]TOTH G.On the structure of convex sets with symmetries[J].Geom Dedicata，2009，143：69-80.

[14]TOTH G.Minimal simplices inscribed in a convex body[J].Geom Dedicata，2014，170：303-318.

[15]TOTH G.A measure of symmetry for the moduli of spherical minimal immersions[J].Geom Dedicata，2012，160：1-14.

三角形与任意单点生成凸包的Minkowski非对称度

国起
（苏州科技学院数理学院，江苏苏州215009）

作为最重要的几何仿射不变量，凸体的非对称度近年来重新引起了众多研究者的关注与研究。文中讨论了平面上一个三角形与任意单点生成凸包的Minkowski非对称度，给出了此类凸体Minkowski非对称度的精确计算公式，并揭示了这类凸体Minkowski非对称度的某些有趣性质。

凸体；Minkowski非对称度；凸包

2015－10－09

国家自然科学基金资助项目（11271282）

国起（1957－），男，山东青岛人，教授，博士，研究方向：泛函分析，凸几何分析，数学形态学。

O18MR（2000）Subject Classification：52A20；52A38；52A39；52A40

责任编辑：谢金春