论离散的Hilbert型不等式及其算子表示
杨必成
(广东第二师范学院 数学系, 广东 广州 510303)
论离散的Hilbert型不等式及其算子表示
杨必成
(广东第二师范学院 数学系, 广东 广州 510303)
引入独立参量及中间变量,应用权系数的方法及实分析技巧,建立离散的、具有最佳常数因子的一般齐次核Hilbert型不等式,还考虑了其等价式、逆式及算子表示式,并计算了一些特殊核算子的范数.
权系数;离散的Hilbert型不等式;等价式;离散的Hilbert型算子;范数
0 引言


(1)


(2)
这里,常数因子π仍为最佳值.
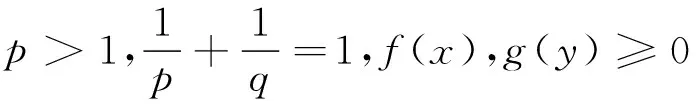

(3)

(4)
并且有下列较为精确的形式:

(5)
式(1)~式(5)是分析学的重要不等式,它们的早期推广应用多见于文献[4-5]中.
1934年, Hardy等把式(3),式(4) 推广为一般-1齐次核k(x,y)的Hardy-Hilbert型不等式(见[4],定理319). 1998年,文[6]引入独立参量λ∈(0,1]及beta函数,推广式(2)为如下形式:
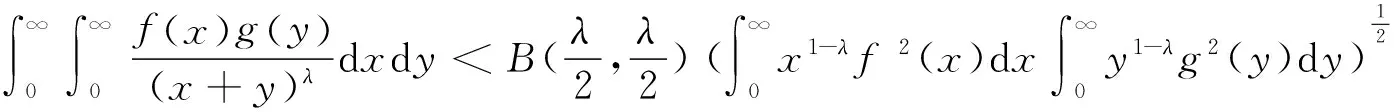
(6)
当λ=1时,式(6)变为式(2).此后数年,不少作者讨论了引入独立参量的若干推广不等式.2003年,文[7]综述了这段时期的研究成果.

(7)

(8)
同时式(4)、式(5)也得到引入独立参量及两对共轭指数的最佳推广(详见[22]).
2006-2007年,文[9-10]等用线性算子刻画Hilbert型不等式及其等价形式.此后,不少作者从不同角度探讨了Hilbert型不等式的各种性态(见[11-19]).2009年,为纪念Hilbert不等式发表100周年,文[20]综述了负数齐次核参量化Hilbert型不等式的研究成果.随后,一些作者开始了对实齐次核及非齐次核的Hilbert型积分不等式的研究(详见[21]). 2009-2012年,杨在专著[22-26]中论述了一般实数齐次核Hilbert不等式及其算子表示的理论,推广了文[4]的工作.
本文引入独立参量及中间变量,应用权系数的方法及实分析技巧,建立离散的具有最佳常数因子的一般齐次核Hilbert型不等式,考虑了其等价式、逆式及算子表示式,还计算了一些特殊核算子的范数.
1 等价不等式


(9)

(10)
(i)若p>1(q>1),有常数k>0,使
ω(λ1,m) (11) ϖ(λ2,n) (12) 则有如下不等式: (13) (ii)若0 ω(λ1,m)>k(1-θ1(m)),m∈N(m≥m0), (14) 则有如下不等式: (15) (iii)若p<0(0 ϖ(λ2,n)>k(1-θ2(n)),n∈N(n≥n0), (16) 则有如下不等式: (17) 证明(i) 当p>1时,配方,并由带权的Hölder不等式[27],有 (18) 由式(12),有 (19) 再由式(11),有式(13). (ii) 当0 [ϖ(λ2,n)]p-1>kp-1(n∈N(n≥n0)), 有式(19)的逆式.由式(14),有式(15). (iii)当p<0时,经同样的配方及由逆向的Hölder不等式,有式(18),再由式(16),注意到 [ϖ(λ2,n)]p-1 有不等式 (20) 由式(11),有式(17).证毕. (i) 若p>1(q>1),有常数k>0,使式(11),式(12)成立,则有式(13)的如下等价不等式: (21) (ii)若0 (22) (iii)若p<0(0 (23) 证明(i) 当p>1时,配方,并由Hölder不等式,有 (24) 再由式(13),有式(21).反之,设式(21)成立.置 (25) 故有式(13).因而式(21)与式(13)等价. (ii)当0 (26) 故有式(15).因而式(22)与式(15)等价. (iii)当p<0(0 (27) 再由式(16),有式(23).反之,设式(23)成立.取 (28) 故有式(16).因而式(23)与式(16)等价.证毕. (29) 由L控制收敛定理[28],有 两式相加可得式(29).证毕. (30) (31) (32) 则可算得 式(32)的常数因子必为最佳值,不然,由式(24)(取k=k(λ1)),必导出式(31)的常数因子也不为最佳值的矛盾.证毕. (33) (34) (35) (36) (37) (38) 由式(29),即有k(λ1)≥K(ε→0+).故K=k(λ1)为式(34)的最佳值. 式(35)的常数因子必为最佳值,不然,由式(26)(取k=k(λ1)),必导出式(34)的常数因子也不为最佳值的矛盾. 由式(29),即有k(λ1)≥K(ε→0+).故K=k(λ1)为式(37)的最佳值. 式(38)的常数因子必为最佳值,不然,由式(27)(取k=k(λ1)),必导出式(37)的常数因子也不为最佳值的矛盾.证毕. 例1 易验证,下列函数 vi(t)=tα(t∈(0,∞);α>0,n0=m0=1),vi(t)=(ln t)α(t∈(1,∞);α>0,n0=m0=2), vi(t)=t-β(t∈(β,∞);0<β<1,n0=m0=1)(i=1,2), 均满足定理3,定理4的相关条件. 评注1若用下列统一条件 (39) (40) 取代式(11),式(12)(取k=k(λ1)),式(33)及式(36),其余不变,则可同时得到定理3,定理4的所有结果. 引理2若在区间I上,函数f(t),v(t),g(t)>0,满足f′(t)<0,f″(t)>0,v′(t)>0,v″(t)≤0,及g′(t)≤0,g″(t)≥0,h(t)∶=f(v(t))g(t),则有h′(t)<0,h″(t)>0. 证明求导数可得 h′(t)=f′(v(t))v′(t)g(t)+f(v(t))g′(t)<0, h″(t)=f″(v(t))(v′(t))2g(t)+f′(v(t))v″(t)g(t)+f′(v(t))v′(t)g′(t)+ f′(v(t))v′(t)g′(t)+f(v(t))g″(t)>0. 证毕. (41) (42) 再由引理2,递减条件及上述变换,由式(41),有 故式(30)及式(33)成立. 由递减条件,又有 再由递减条件及上述变换,由式(42),有 故式(36)成立. 由定理2,定理3,本定理的结论成立.证毕. (43) (44) 当然可求得其他逆向不等式. (45) (46) 严格递减且严格凸,由Hermite-Hadamard不等式[27],有 类似于定理5的证明,由递减条件,上述变换及式(45),有 故式(30)及式(33)成立. 同理,由递减及凸条件,又有 类似于定理5的证明,由递减条件,上述变换及式(42),有 故式(36)成立. 由定理2,定理3,本定理的所有结论都成立.证毕. (47) (48) 当然亦可求得其他逆向不等式. (49) (50) 当然可求得其他逆向不等式. (51) 因有 故得 可算得 (52) (53) (54) 其他相应的逆向不等式也可求得. (55) (56) 由定理3,定理4及评注1,有 (57) (58) (i)若p>1,则有如下等价不等式: (59) (60) (ii)若0 (61) (62) (iii)若p<0,则有如下等价不等式: (63) (64) 这里,常数因子k(λ1)都是最佳值. 注若只考虑p>1的情形,则式(57)的左边不要求取严格不等号. (65) 于是,式(60),式(61)可写成如下等价的算子表示式: (Ta,b) (66) ||Ta||p,ψ1-p (67) 定义算子范数为 (68) 因由定理7或定理8,式(67)的常数因子是最佳值,故 ||T||=k(λ1). (69) 对x>0严格递减; 对y>0严格递减.可算得 (70) 因有 故求导数得 (71) 当m=1时, [1] WEYL H. Singulare integral gleichungen mit besonderer berucksichtigung des fourierschen integral theorems[M]. Gottingen :Inaugeral-Dissertation,1908. [2] SCHUR I. Bernerkungen sur theorie der beschrankten Billnearformen mit unendlich vielen Veranderlichen[J].J Math,1911,140:1-28. [3] HARDY G H. Note on a theorem of Hilbert concerning series of positive terms[J]. Proceedings London Math Soc,1925,23(2):Records of Proc xlv-xlvi. [4] HARDY G H,LITTLEWOOD J E,POLYA G. Inequalities[M]. Cambridge:Cambridge Univ Press,1952.[5] MITRINOVIC D S,PECARIC J E,FINK A M. Inequalities involving functions and their integrals and derivatives[M]. Boston:Kluwer Academic Publishers,1991. [6] YANG Bi-cheng. On Hilbert′s integral inequality[J]. Journal of Mathematical Analysis and Applications,1998,220:778-785. [7] YANG Bi-cheng,RASSIAS Th M. On the way of weight coefficient and research for Hilbert-type inequalities[J],Math Ineq Appl,2003,6(4):625-658. [8] YANG Bi-cheng. On an extension of Hilbert′s integral inequality with some parameters[J]. The Australian Journal of Mathematical Analysis and Applications,2004,1(1):1-8. [9] YANG Bi-cheng. On the norm of an integral operator and application[J]. Journal of Mathematical Analysis and Applications,2006,321:182-192. [10] YANG Bi-cheng. On the norm of a Hilbert′s type linear operator and applications[J].J Math Anal Appl,2007,325:529-541. [11] YANG Bi-cheng,BRNETIC I,KRNIC M,et al. Generalization of Hilbert and Hardy-Hilbert integral inequalities[J]. Math Ineq and Appl,2005,8(2):259-272. [12] KRNIC M,PECARIC J E. Hilbert′s inequalities and their reverses[J].Publ Math Debrecen,2005,67(3-4):315-331. [13] HONG Yong. On Hardy-Hilbert integral inequalities with some parameters[J].J Ineq in Pure & Applied Math,2005,6(4):1-10. [14] ARPAD B,CHOONGHONG O. Best constant for certain multi linear integral operator[J].Journal of Inequalities and Applications,2006,no. 28582. [15] KUANG Ji-chang,DEBNATH L. On Hilbert′s type inequalities on the weighted Orlicz spaces[J].Pacific J Appl Math,2007,1(1):95-103. [16] LI Yong-jin,HE Bing. On inequalities of Hilbert′s type[J]. Bulletin of the Australian Mathematical Society,2007,76(1):1-13. [17] ZHONG Wu-yi,YANG Bi-cheng. On multiple Hardy-Hilbert′s integral inequality with kernel[J]. Journal of Inequalities and Applications,2007,Art ID 27962,17 pages,doi:10.1155/2007/27. [18] YANG Bi-cheng,CHEN Qiang. A half-discrete Hilbert-type inequality with a homogeneous kernel and an extension[J]. Journal of Inequalities and Applications,2011:124,doi:10.1186/1029-242X-2011-124. [19] YANG Bi-cheng. A half-discrete Hilbert-type inequality with a non-homogeneous kernel and two variables[J]. Mediterranean Journal of Methematics,2012,doi:10.1007/s00009- 012- 0213-50 online first. [20] 杨必成.参量化的Hilbert型不等式研究综述[J].数学进展,2009,38(3):257-268. [21] 杨必成. 一个Hilbert型积分不等式[J].浙江大学学报(理学版),2007,34(2):121-124. [22] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009. [23] YANG Bi-cheng. Hilbert-type integral inequalities[M].Sharjah:Bentham Science Publishers Ltd,2009. [24] YANG Bi-cheng. Discrete Hilbert-type inequalities[M].Sharjah:Science Bentham Publishers Ltd,2011. [25] YANG Bi-cheng. Hilbert-type integral operators:norms and inequalities[M]//Nonlinear analysis,stability,approximation,and inequalities,PARALOS P M,et al.New York:Springer,2012:771-859. [26] YANG Bi-cheng. Two kinds of multiple half-discrete Hilbert-type inequalities[M].Berlin:Lambert Academic Publishing,2012. [27] 匡继昌.常用不等式[M].济南:山东科技出版社,2004. [28] 匡继昌.实分析与泛函分析(续论)(上册)[M].北京:高等教育出版社,2015. On Discrete Hilbert-Type Inequalities and their Operator Expressions YANG Bi-cheng (Department of Mathematics, Guangdong University of Education, Guangzhou,Guangdong, 510303, P. R. China) By introducing independent parameters and interval variables, applying the way of weight coefficients and technique of real analysis, a discrete Hilbert-type inequality with the general homogeneous kernel and a best possible constant factor is provided. Furthermore, the equivalent forms, the reverses, the operator expressions with the norms and some particular examples are considered. weight coefficient; discrete Hilbert-type inequality; equivalent form; discrete Hilbert-Type operator; norm 2016-05-28 国家自然科学基金资助项目(61370186) 杨必成,男,广东汕尾人,广东第二师范学院数学系教授. O178 A 2095-3798(2016)05-0001-20


















2 最佳常数因子









































3 两类递减核的不等式







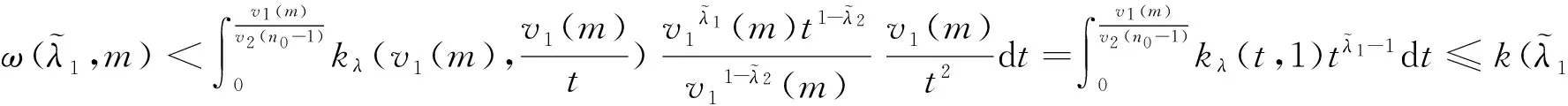
























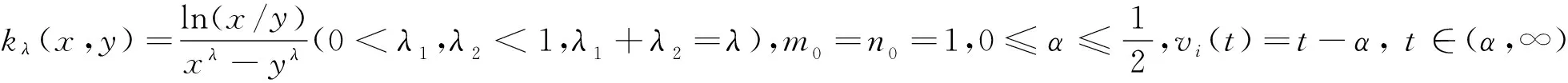




4 应用定理3、定理4的例







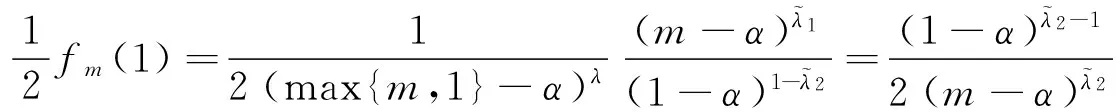


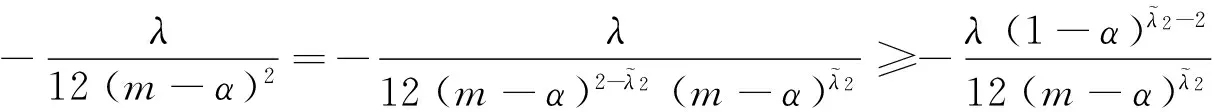


五 不含中间变量的一些特殊结果

















6 算子表示及一些特例