Algebraic Dynamics Study a Single Molecule Driven by a Time Dependent Laser Radiation Field

ZHU Qin-sheng， DING Chang-chun， LI Yong-zhang， WU Shao-yi， and WU Hao

（1. School of Applied Physics， University of Electronic Science and Technology of China Chengdu 610054；2. University of Glasgow， University of Electronic Science and Technology of China Chengdu 610054）

Algebraic Dynamics Study a Single Molecule Driven by a Time Dependent Laser Radiation Field

ZHU Qin-sheng1， DING Chang-chun1， LI Yong-zhang2， WU Shao-yi1， and WU Hao1

（1. School of Applied Physics， University of Electronic Science and Technology of China Chengdu 610054；2. University of Glasgow， University of Electronic Science and Technology of China Chengdu 610054）

The dynamical properties of a single molecule driven by a time dependent laser radiation field are researched. Based on the su（1，1）（3）h⊕ （（3）his Heisenberg algebra） dynamical symmetry structure of the system，the exact solutions of the system is obtained by using the algebraic dynamics method. The shift between the frequency Ω of the laser radiation field and the molecule vibration frequency ω under resonance phenomenon is studied.

adiabatic energy levels； algebraic dynamics； geometric phase； resonance

Algebraic dynamics is a theory which studies the quantum system by the algebraic method［1-7］. It always use the group relationship of the system operators or group structure of the system to discuss the properties of the system. In the past years， it has been extensively used in nuclear physics for many autonomous systems. However， many systems are non-autonomous which depend on time in many experiments. So， It's necessary to extend the theory of algebraic dynamics to resolve the non-autonomous problems because it can help us control the systems. Several typical non-autonomous quantum systems have been researched by the method of dynamical algebras， e.g. the su（1，1） dynamic structure for the particle moving in time dependent Paul trap［8］， the polarization of spin particle in accelerator forms a su（2） dynamic system［9］，the spin particle in a rotating magnetic field， and the Berry phase of a laser in helical optical fiber forming a su（2） dynamic system［10-16］. As an important controlling and measurement method for particles and substance， the laser radiation field is always chosen by people［17-19］. When the laser radiation field interacts with particles or substance， an important physical phenomenon， resonance excitation effect will occur. By this physical phenomenon， human can understand many important properties of the particles and substance， such as molecular structure and vibration frequency of the substance. Since the laser radiation fields always depend on time， these quantum system become the non-autonomous quantum system and are accompanied with the resonance excitation effects. So，it is interesting to research the diabatic energy andgeometric phase［20-22］under the resonance excitation phenomena.

In this work， we research the properties of the single molecule which is driven by a time dependent laser radiation field. Firstly， we analyze the su（1，1）（3）h⊕（（3）his Heisenberg algebra） Lie algebraic structure of this system. Secondly， the exact solution of the system has been obtained by the use of algebraic dynamics method. Finally， based on the exact solutions， we study the changing properties of the diabatic energy levels and the geometric phase. Simultaneously， we show that there exists a shift between the laser frequency and the vibration frequency of the molecule when the resonance excitation occurs.

1 The Model Hamiltonian and Algebraic Structure

A single molecule is driven by a time dependent laser radiation field， and the system Hamiltonian is described by the following model which represents a charged harmonic oscillator in a laser radiation field：

where q is the molecule charge； c is velocity of light， the oscillator potential of the molecule isB0is a constant which describes the magnetic field amplitude of the laser electromagnetic field and directs the z axis； ε0and Ω are electric field amplitude and frequency of the laser electromagnetic field respectively.

Where the parameters are： dynam

（4）Through （3） we find that the system has thedynamical algebraic structure su（1，1）⊕h（3）［23］. It canbe checked that： 1）+，0and-span su（1，1） Lie algebra. 2）1，2and 1 spanh（3） （h（3）is Heisenberg algebra） Lie algebra. 3）It satisfy the following communication relations （=1）：

Simultaneously， the generators of su（1，1） and h（3）also satisfy the following communication relations：

From （4） we know that the system has the dynamical algebraic structurehω（4）［24］for the parameters X1=X2=X（t）=0（B0=0）.

2 The Exact Solutions of the System Using the Algebraic Dynamic Method

The time-evolution of the system satisfy the time-dependent Schrödinger equation：

Adopting the solving steps of algebraic dynamics［12-16］， firstly， introduce the gauge transformation：

where v（t），v2（t），v1（t），v-（t）and v0（t）are all time-dependent parameters.

The Schrödinger equation under the gauge transformation （7） （=1） becomes：

Here the gauged Hamiltonian is given by：

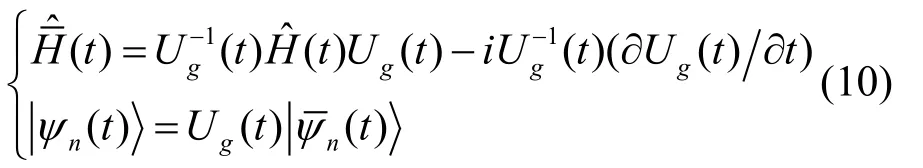
Substituting （3） and （7） into （9）， after some complex calculations， one has：

Here the coefficients of （11） are：

Because we can choose the appropriate transformation which is one of the advantages of algebraic dynamics［9-15］to simplify the calculation，which is also easy to find the Cartan operators， the best choice of the gauge transformation satisfies the following conditions：

After some calculation， the solutions of the parameters of （13） can be obtained as follows：

Here， consider the initial conditionsv（0）=0，v2（0）=0，v1（0）=const，v-（0）=0and v0（0）=0.

Putting （13） to （10）， we obtain the covariant Hamiltonian：

Where：

The Cartan operatorI（0） does not depends on time explicitly and has the standard form of harmonic oscillator. So， the time-dependent dynamical symmetry can be covered into the stationary dynamical symmetry by choosing a proper gauge transformation.

The eigen problems of the Cartan invariant operatorcan be obtained. Let nbe the eigenstate ofˆ（0）（here n is the quantum number of the standard form of harmonic oscillator），namely：

so the eigenvalues and eigenstates are：

So the covariant Schrödinger equation （9） has the following solutions：

where：

In order to obtain the solutions of （7）， firstly， we need to rewriteunder the coordinate x representation as follows：

Secondly， using the following relations

The orthonormal nonadiabatic basis can be directly obtained and given as follows：

The equation describes a motion of quasiharmonic oscillator in coordinate space and the origin of this coordinate space constantly moves and stretches. At the same time， there are a collective velocity potential v2（t）x and a time-dependent phase factor for this system.

The general solutions of the time-dependent Schrödinger equation （7） can be expanded by the nonadiabatic basis：

where Cpypznis an expansion coefficient that is not dependent on time. All the dynamical information is included in the nonadiabatic basis.

3 The Diabatic Energy Levels of the System

Using （10）， （14）， （15）， the diabatic energy levels of the system can be obtain by：

From（24）， it is easily found： 1） the change of the diabatic energy levels comes from the factor2） the changing approach of the diabatic energy levels are quasi-periodic due to the periodic changing parameters parametersand （v）t.

To better understand the properties of the diabatic energy levels， the changing behaviors are shown in Fig. 1 （Here， the parameters n=0，ω=2100cm-1，px=1，py=0 ,m=1×10-27,q=1 and ε01=）.The diabatic energy level shows an abrupt increase when the laser frequency Ω arrives about 2 100 cm-1，corresponding to “the resonance absorption effect of molecular”， and the different peaks display the different magnetic field amplitudes B0. Simultaneously， with the increasing of the magnetic field amplitude B0， the laser frequency Ω diverges from the molecule vibration frequencyω， which is characterized by the peak-shifting of the resonance absorption. The above results may be helpful for the explanation of laser-induced effect of biological genetic variation［25］， e.g. the bond of biological genetic may be broken and recombined which is aroused by the resonance absorption effect.

Fig. 1 The change of diabatic energy levels

It is surprising why the resonance phenomenon occurs. The results stem from the parameters v1（t），v2（t） and v（t） （see （26））. From （15） we find that the changing period of the parameters v1（t），v2（t） and（v）t not only depends on the Ω， but also on k′which depends on the ω and B0. So the above reasons lead to resonance phenomenon and a divergence between Ω andω. Moreover， from the parameters k′ and A in （15）， we know that： 1） the shift of the resonance frequency increases with the decrease of the ω and the increase of the B0； 2） The peak value displays different for different B0.

4 Geometric Phase of the System

The system states will acquire a total phase which composes of the dynamical phase and the geometric phase when the parameters of the system go through a time-dependent evolution. The dynamical phase depends both on the path and on the rate of the path，while the geometric phase depends on the influence of the external environment or the interaction with the background.

The dynamical phase γd［2-3，24］is：

The geometric phase β［2-3，24］is：

where the total phase γ0-tis：

where Θpypzn（t） is the total phase ofis the phase induced by the gauged transformation， and γI=-（v1（t）2（t）+（t））.

In order to further study the changing properties of the geometric phase， we calculate the geometric phase for n=0，1 respectively.

For n=0，the geometric phase is：

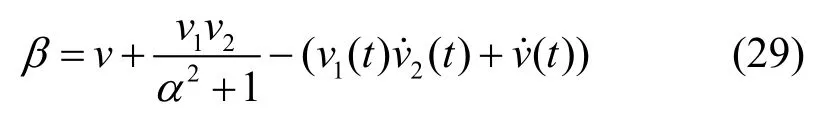
For n=1， the geometric phase is：

Where θ is the phase angle of the complex number

Contrasting （30） and （31）， it is easy to know that the difference of the Berry phase is aroused by the θ for n=0 and n=1. Because the phase angle θ depends on the parametersv1（t），v2（t） andα， it shows the quasi-periodic changing behavior and depend on the value of ω and B0.

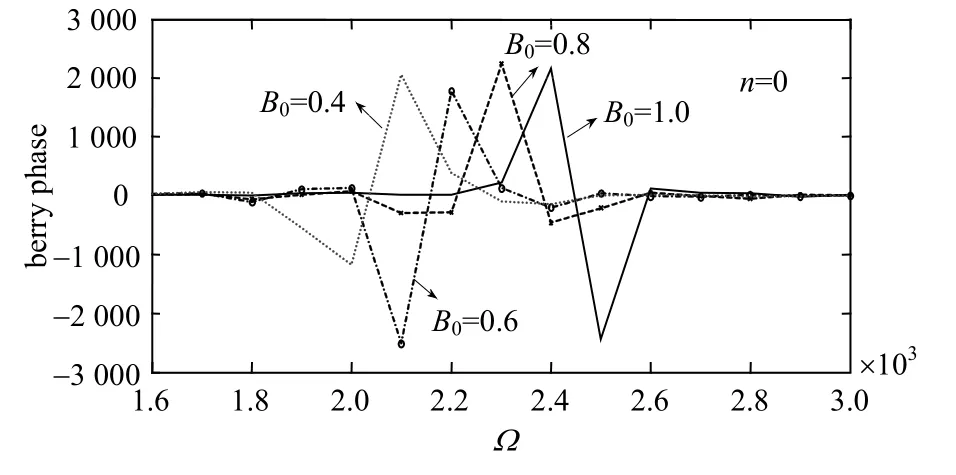
Fig. 2 The change of geometric phase

Fig. 3 The change of the geometric phase

The changing of the geometric phase β are shown in the Fig. 2 and Fig. 3 for n=0 and n=1 respectively （The related parameters are same as Fig.1）. We found that： 1） The geometric phase β also presents resonance phenomenon when the laser frequency Ω gets about 2 100 cm-1. 2） Similar to the diabatic energy level， there also exists a shift of the peak of the resonance for the difference between the laser frequency Ω and the molecule vibration frequencyω. 3） With the increase of the magnetic field amplitude B0， the shift of the peak of the resonance increases. 4） The influence of the phase angle θ is small for n=0 and n=1. The results stem from the changing period of the parameters v1（t），v2（t） and（v）t are dependent on the k′ and Ω . Simultaneously， the parameters k′ and A depend on the ω and B0. It arouses that the shift of the resonance frequency increases with the decrease of the ω and the increase of the B0.

5 Conclusion

Based on su（1，1）⊕h（3）dynamical symmetry of the molecule which is driven by a time dependent laser radiation field， we obtain the exact solutions of the system by use of algebraic dynamics and further discuss the changing properties of the diabatic energy levels and geometric phase. It is found that there exists the resonance phenomenon for the diabatic energy levels and geometric phase when the resonance frequency Ω is close to the molecular vibration frequency ω， and a divergence which depends on the magnetic field amplitude B0exists between Ω and ω. The present work may be helpful for the explanation of laser-induced effect of biological genetic variation， and it shows that the method of dynamical algebras is useful for the study non-autonomous quantum system which has some algebraic structures.

Acknowledgments

The work was supported by UOG-UESTC Joint school educational innovation program of university of electronic science and technology of China（GL2014001）

Reference

［1］ BARUT A ， BOHM A， NE'EMAN Y. Dynamical groups and spectrum generating algebras［M］. Singapore： World Scientific， 1988： 3-69.

［2］ BIRMAN J L， SOLOMON A I. Spectrum generating algebras in condensed matter physics［M］. Singapore： World Scientific， 1988： 317-339.

［3］ BIRMAN J L， SOLOMON A I. Dynamical group so（6） and coexistence： Superconductivity and charge-density waves［J］. Physical Review Letter， 1982（49）： 230-233.

［4］ SOLOMON A I. Group theory of superfluidity［J］. Journal of Mathematical Physics， 1971（12）： 390-393.

［5］ SOLOMON A I， BIRMAN J L. Dynamical group model of the CDW state［J］. Physical Review Letter， 1982， 88A：413-416.

［6］ WYBOURNE B G. Classical groups for physicists［M］. New York： Wiley， 1974.

［7］ WANG S J. The study of the theory of the man-made quantum systems and algebraic dynamics［J］. Progress in Physics， 1999（19）： 331-370.

［8］ PAUL W. Electromagnetic traps for charged and neutral particles［J］. Review of Modern Physics， 1990（62）： 531-540.

［9］ WANG S J， ZUO W， WEIGUNY A， et al. Exact solution of the linear nonautonomous system with the SU（1，1） dynamical group［J］. Physics Letter A， 1994（196）： 7-12.

［10］ WANG S J. Nonadiabatic Berry's phase for a spin particle in a rotating magnetic field［J］. Physical Review A，1990（42）： 5107-5110.

［11］ WANG S J， CEN L X. Exact solution of the L-S coupled system in a time-dependent magnetic field［J］. Physical Review A， 1998（58）： 3328-3331.

［12］ CEN L X， QI L X， JING Y Y， et al. Evaluation of holonomic quantum computation： adiabatic versus nonadiabatic［J］. Physical Review Letter， 2003（90）： 147902.

［13］ WANG X Q， CEN L X. Resolving time-dependent quantum systems via the concatenated cranking procedure：Methods and applications［J］. Physics Letter A， 2011，375（23）： 2220-2223.

［14］ ZHU Q S， KUANG X Y， TAN X M. Algebraic dynamics study for homotrinuclear linear spin cluster in a rotating magnetic field［J］. Physical Review A， 2005（71）： 064102.

［15］ ZHU Q S， LAI W， WU D L. Dynamical symmetry method investigates the dissipation and decoherence of the two-level jaynes-cummings model［J］. Z Naturforsch A，2012， 67a： 559-566.

［16］ WANG S J， LI F L， WEIGUNY A. Algebraic dynamics and time-dependent dynamical symmetry of nonautonomous systems［J］. Physics Letter A， 1993（180）： 189-196.

［17］ STENHOLM S. Foundations of laser spectroscopy［M］. New York： Wiley， 1984.

［18］ MARGCUSE D. Engineering quantum electrodynamics［M］. New York： Academic Press， 1981.

［19］ EBERLY J H， LABROPOULOS P. Multiphoton processes［C］//Proceedings of the International Conference at the University Rochester. New York： Wiley， 1977.

［20］ PANCHARATNAM S. Generalized theory of interference，and its applications. I. Coherent pencils［J］. Proceedings of the Indian Academy of Science， 1956（44）： 247-262.

［21］ BERRY M V. Quantal phase factors accompanying adiabatic changes［J］. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences， 1984， 392：45-57.

［22］ SIMON B. Holonomy， the quantum adiabatic theorem， and Berry's phase［J］. Physical Review Letter， 1983， 51：2167-2170.

［23］ YING Z J， WANG S J， ZHANG W Z. Exact solution to landau system with time-dependent electromagnetic fields［J］. Chinese Physics Letter， 1999， 16： 391-393.

［24］ ZHANG C X， ZHU Q S， KUANG X Y. Resonance excitation effect for a molecule driven by a laser radiation field： Algebraic dynamics method to determine the diabatic energy levels and geometric phase［J］. Physics Letter A，2007（371）： 354-359.

［25］ KEVIN K， SCHUMAN J S， LOEWEN N A. Outcomes of ab interno trabeculectomy with the trabectome by degree of angle opening［J］. British Journal of Ophthalmology，2014， 99（7）： 914-919.

编 辑 叶 芳

代数动力学研究含时激光辐射场驱动下的单分子

朱钦圣1，丁长春1，李咏章2，邬劭轶1，吴 昊1
（1. 电子科技大学物理电子学院 成都 610054；2. 电子科技大学格拉斯哥学院 成都 610054）

该文研究了含时激光辐射场驱动下的单分子系统的动力学性质。基于系统的su（1，1）（3）h⊕代数结构（（3）h满足Heisenberg代数）和代数动力学方法，不仅获得了系统的解析解，而且还研究了系统的非绝热能级和几何相位。最后研究了非绝热能级和几何相位与激光辐射场频率的函数关系，展示了系统存在的共振现象以及分子共振吸收时激光辐射场频率和分子振动频率之间的漂移现象。

非绝热能级； 代数动力学； 几何相位； 共振

O413

A

10.3969/j.issn.1001-0548.2016.02.009

2015 - 12 - 11；

2016 - 02 - 26

朱钦圣（1978 - ），男，博士，主要从事量子信息方面的研究.

date：2015 - 12 - 11；Revised date：2016 - 02 - 26

Biography：ZHU Qin-sheng was born in 1978， and his research interests include quantum information.