Stein方程数值解的黎曼梯度算法
段晓敏, 赵新玉, 孙华飞
(1.大连交通大学 材料科学与工程学院,辽宁,大连 116028;2.大连交通大学 理学院,辽宁,大连 116028;3.北京理工大学 数学学院,北京 100081)
Stein方程数值解的黎曼梯度算法
段晓敏1,2, 赵新玉1, 孙华飞3
(1.大连交通大学 材料科学与工程学院,辽宁,大连 116028;2.大连交通大学 理学院,辽宁,大连 116028;3.北京理工大学 数学学院,北京 100081)
基于正定矩阵流形的信息几何结构, 使用黎曼梯度算法来获得Stein方程的数值解. 利用弯曲的黎曼流形上的测地距离作为算法的目标函数,并将流形上的测地线作为算法的收敛路径. 通过数值实验讨论了算法的步长和收敛速度的关系,从而得到算法的最优步长.
Stein方程;黎曼梯度算法;数值模拟
考虑Stein矩阵方程
(1)
式中:A为任意的n×n实矩阵;Q为给定的n×n正定矩阵;X为待求的未知矩阵. 它在许多领域中起着重要的作用,如系统与控制理论、动态规划等科学与工程计算领域[1-3]. 在过去几十年里,人们对这个方程的求解问题进行了各种研究,例如,Bartels-Stewart方法,Hessenberg-Schur方法,Schur方法和QR分解法[1]. 根据偏序集上的Kronecker内积和固定点原理,文献[4]讨论了方程存在唯一正定矩阵解的充分条件,即,如果I-ATA是一个正定矩阵, 那么方程(1)存在唯一的解, 并且这个解是对称正定的矩阵, 其中I为n阶单位矩阵.
信息几何是在黎曼流形上采用现代微分几何方法来研究统计学和信息领域问题而提出的一套新的理论体系,已经逐步应用于神经网络、信号处理、系统与控制等领域[5]. 而将信息几何理论应用到研究矩阵方程的数值解法却很少[6]. 本文将应用信息几何方法求解方程(1)的数值解问题. 注意到解是一个对称正定矩阵, 并且所有的对称正定矩阵的集合构成了一个流形,因此借助于流形的几何结构来研究这个矩阵的数值解更为方便. 为了满足这样的需要,提出解方程(1)的黎曼梯度下降法, 使用弯曲的黎曼流形上的测地距离作为目标函数, 并且把测地线作为算法的收敛路径. 最后, 用两个数值例子演示黎曼梯度下降法的有效性.本文中, 用X>0表示X是对称正定的矩阵. 如果X-Y>0, 将会用X>Y表示.
1 预备知识
本节简要介绍黎曼流形上的几何概念、黎曼梯度下降算法以及正定矩阵流形的几何结构,详细内容见文献[7-8].
1.1 黎曼流形上的几何概念


给定一个正则函数f:M→R, 以向量V∈TXM为方向的黎曼梯度Xf代表f沿着V的变化率. 也就是说, 给定任何光滑曲线φX,V:[0,1]→M, 使其满足φX,V(0)=X∈M和X,V(0)=V, 那么黎曼梯度Xf是TXM上唯一满足下式的切向量
一些光滑流形上的优化问题可以利用黎曼梯度下降法来解决[9]. 因此, 考虑流形M上的微分方程
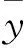
在考虑黎曼流形M上的优化算法时要考虑到流形的几何特征. 具体地, 从初始值X0开始, 设在迭代算法的步骤t∈N时刻, 算法的迭代点为Xt∈M. 利用文献[9]的方法, 可以将Xt沿着测地线,向目标函数J(Xt)的黎曼梯度的反方向移动,则得到下一个点Xt+1. 也就是说,如果设目标函数J(Xt)沿着Xt方向的黎曼梯度为
那么黎曼梯度下降算法可以表示为
式中η为能够使得算法收敛的任何合适的步长.
1.2 正定矩阵流形的几何结构
所有的n×n对称正定矩阵可以构成一个流形,记为P(n). 流形P(n)不是一般线性群GL(n)的李子群,而是GL(n)的一个子流形. 在流形P(n)上,可以定义不同的度量,这将赋予它不同的几何结构. 设所有n×n对称矩阵组成的集合为S(n),那么P(n)的切空间为S(n). 即任何对称矩阵的指数映射都是一个正定矩阵,并且任何正定矩阵的对数映射都是一个对称矩阵.设所有n×n实矩阵组成的集合为M(n),把流形P(n)视为M(n)的一个子集,那么Frobenius内积定义为
式中:B1,B2∈P(n).Frobenius内积是欧氏的,不依赖于点的选择. 这个内积导致了P(n)是一个平坦的黎曼流形. 而且测地线是直线,还有一定的限制条件. 在流形P(n)上改进的Frobenius内积在B处的定义为
(2)
式中X,Y∈S(n). 于是, 带有黎曼度量(2)的流形P(n)成为了黎曼流形, 而且, 它使得黎曼流形P(n)是弯曲的.
2 黎曼梯度算法
如果A满足
(3)
那么,方程(1)的解是唯一正定的[2]. 设L(X):=Q+ATXA,显然,对任何的X∈P(n),L(X)是一个正定矩阵. 本文目标是寻找一个矩阵X∈P(n)使得L(X)与给定的矩阵Q越接近越好.注意到黎曼流形P(n)是测地完备的, 因此用Q和L(X)的测地距离作为目标函数J(X)
那么,方程(1)的精确解可以被定义为
(4)
为了求得J(X)的最小值点, 利用微分方程, 显然最小值在X*处实现, 它满足

(5)
那么黎曼梯度下降算法可以表示为
(6)
式中η为能够使得算法(6)收敛的任何合适的步长.
为了使用算法式(5)(6),首先需要计算目标函数J(Xt)的黎曼梯度. 根据黎曼梯度的定义, 获得如下定理.
定理1 目标函数J(X)在X处的黎曼梯度为
证明 计算实值函数

根据文献[4]的性质2.1以及一些矩阵迹的性质有
事实上, 因为
对∀A∈GL(n)和∀B∈P(n)成立, 那么XJ(X)可以被重写为
证毕.
综上, 黎曼梯度下降算法(RGA)为
式中初值X0∈P(n). 为了使RGA算法具有快速的收敛速度, 步长η可以通过实验得到, 细节将在模拟实例中给出.
3 例 证
本章给出两个例子说明黎曼梯度算法(RGA)的计算有效性. 模拟中的误差设ρ(L(X))=Q<10-15,其中ρ(·)表示矩阵的谱半径.
例1 首先考虑当n=5时,Stein方程
Q=X-ATXA
的数值解, 式中:
Q=
A=
它们满足前提条件式(3).
在下面的模拟中, 使用RGA算法取5阶单位阵作为初值X0. 将步长大小和收敛速度的关系用图1表示出来. 可以发现, 当步长从0变化到0.54时, 迭代次数逐渐减少, 步长比0.54大时算法收敛速度又变慢了. 因此, 通过实验, 临界值0.54被选为RGA算法的步长.
经过Matlab程序计算, 需要32次迭代得到方程的数值解为
针对这组数据算法的收敛速度请见图2.
例2 考虑10阶的Stein矩阵方程, 其中Q∈P(10),A满足条件(3). 类似上节的计算过程, 选择最优步长为0.52,模拟结果显示RGA算法需要11次迭代, 计算时间为0.002 5 s.
4 结 论
借助于正定矩阵流形的信息几何结构,利用黎曼梯度算法求解Stein方程的数值解.这个算法使用弯曲的黎曼流形上的测地距离作为目标函数, 并将流形上的测地线作为算法的收敛路径.为了给出最快的收敛速度, 优化的步长被给出. 最后通过两个数值例子表明黎曼梯度下降法求解Stein方程数值解的有效性.
[1] Gajic Z, Qureshi M T J. Lyapunov matrix equation in system stability and control[M]. [S.l.]: Courier Corporation, 2008.
[2] Heinen J. A technique for solving the extended discrete Lyapunov matrix equation[J]. IEEE Transactions on Automatic Control, 1972,17(2):156-157.
[3] Ran A C M, Reurings M C B. The symmetric linear matrix equation[J]. Electronic Journal of Linear Algebra, 2002,9(16):93-107.
[4] Ran A C M, Reurings M C B. A fixed point theorem in partially ordered sets andsome applications to matrix equations[J]. Proceedings of the American Mathematical Society, 2003,132:1435-1443.
[5] Amari S, Nagaoka H. Methods of information geometry[M]. Oxford: Oxford University Press, 2000.
[6] Duan X, Sun H, Peng L, et al. A natural gradient algorithm for the solution of discrete algebraic Lyapunov equations based on the geodesic distance[J]. Applied Mathematics and Computation, 2013,219:9899-9905.
[7] Moakher M. A differential geometric approach to the geometric mean of symmetric positive-definite matrices[J]. SIAM Journal on Matrix Analysis and Applications, 2005,26(3):735-747.
[8] Spivak M. A comprehensive introduction to differential geometry[M]. 3rd ed. Berkeley: Publish or Perish, 1999.
[9] Udriste C. Convex functions and optimization methods on Riemannian manifolds[M]. Berlin: Springer Science & Business Media, 1994.
(责任编辑:李兵)
Riemannian Gradient Algorithm for the Numerical Solution of Stein Equations
DUAN Xiao-min1,2, ZHAO Xin-yu1, SUN Hua-fei3
(1.School of Science, Dalian Jiaotong University, Dalian,Liaoning 116028, China;2.School of Materials Science and Engineering, Dalian Jiaotong University, Dalian,Liaoning 116028, China;3.Mathematical School, Beijing Institute of Technology, Beijing 100081, China)
A Riemannian gradient algorithm based on information geometric structures of a manifold consisting of all symmetric positive-definite matrices was proposed to calculate the numerical solution of Stein equations. In this algorithm, the geodesic distance on the curved Riemannian manifoldis taken as an objective function and the geodesic curve was treated as the convergence path. Also the optimal variable step-sizes corresponding to the minimum value of the objective function were provided in order to improve the convergence speed.
Stein equation; Riemannian gradient algorithm;simulation
2015-07-03
国家自然科学基金资助项目(61401058, 61179031);中国博士后科学基金面上资助项目(2015M581323)
段晓敏(1979—),女,博士,讲师,E-mail:dxmhope@djtu.edu.cn;赵新玉(1979-),男,博士,副教授,E-mail:xyz@djtu.edu.cn.
孙华飞(1958—),男,教授,博士生导师,E-mail:huafeisun@bit.edu.cn.
O 186
A
1001-0645(2016)02-0201-04
10.15918/j.tbit1001-0645.2016.02.018

