两类非对称量子码的构造
马月娜, 冯晓毅, 苏志忠, 刘杨2,
1.西北工业大学 电子信息学院, 陕西 西安 710072; 2.空军工程大学 理学院, 陕西 西安 710051 3.空军第一航空学院 训练部, 河南 信阳 464000
两类非对称量子码的构造
马月娜1,2, 冯晓毅1, 苏志忠3, 刘杨2,3
1.西北工业大学 电子信息学院, 陕西 西安 710072; 2.空军工程大学 理学院, 陕西 西安 710051 3.空军第一航空学院 训练部, 河南 信阳 464000
通过分圆陪集确定出q2-元域上2个嵌套的BCH码满足Hermite对偶包含的条件;利用这些满足Hermite对偶包含条件的本原BCH码构造出两类非对称量子码的参数,使构造出的码具有较大的z-距离,而且其参数优于已有文献中的结论,从而提高了码的纠错能力。
非对称量子码;BCH码;Hermite对偶包含;CSS构造法
量子纠错码在量子容错计算与量子通信等量子信息处理中发挥着重要作用。然而在量子信息的传输过程中,由于传输信道的不同可导致比特错误σx和相位错误σz出现的可能性也不尽相同,于是,人们针对量子信道中错误类型的非对称特征,提出了一种新的量子纠错码——非对称量子纠错码[1-4]。q-元非对称量子[[n,k,dz/dx]]q码可以控制所有⎣(dx-1)/2」个比特错误和⎣(dz-1)/2」个相位错误。与此同时,可以检测出dx-1个比特错误和dz-1个相位错误,因此dz和dx的取值决定了码的检错和纠错能力[5-8]。Ioffe和Mezard[5]根据比特错误和相位错误出现的不同频率,以及对纠错能力的不同要求,借鉴标准量子纠错码的构造方法,构造出了非对称量子纠错码,使其具有更好的纠错效率;Aly和Sarvepalli等[6-9]将标准量子纠错码的CSS构造法推广到非对称量子纠错码,利用非本原狭义BCH码和RS码构造出很多参数优良的非对称量子纠错码;在此基础上,Wang Long等[10]将非加性标准量子码的特性推广到非对称情形,建立了非对称量子码和经典纠错码之间的关系;Ezerman等[11-12]将CSS构造法加以推广,给出CSS-like构造法,利用该方法和嵌套的自正交线性码构造出一系列新的非对称量子纠错码;La Guardia[13-15]利用两类具有对偶包含关系的BCH码构造出一系列二元和非二元的非对称量子纠错码,这些码的参数优于已有的量子纠错码的参数。陈建章等人[16]利用常循环码和非本原BCH码构造出一些参数优良的非对称量子码。
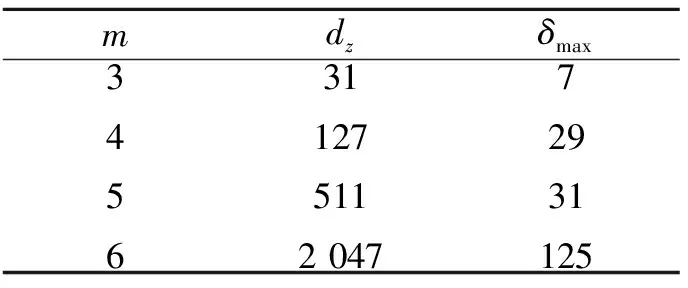
本文在m分别为2l+1(l≥1)和2l(l≥2)2种情况下,利用q2-元域上码长为n=22m-1的本原狭义BCH码构造两类非对称量子码的参数,使构造出的非对称量子码的z-距离远大于δmax,其中δmax=qm+1-q2+1(m=2l)和δmax=qm-1(m=2l+1)分别是对偶包含狭义BCH码的最大设计距离。
1 预备知识
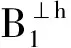
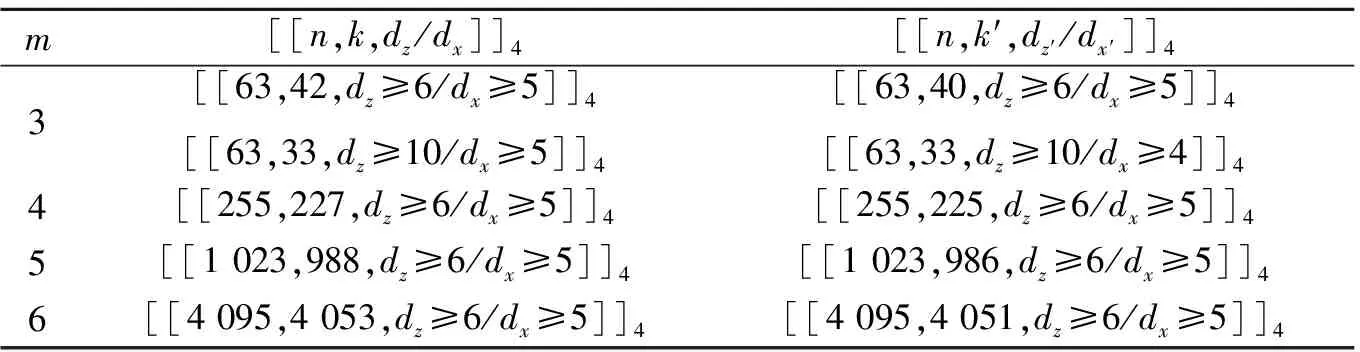
定义1 设q为素数的幂,n>1为正整数且gcd(n,q)=1。若x为正整数且满足x 定义2 设Fq2为q2-元域,ξ为Fq2扩域上的n次本原单位根,若T=Cb∪Cb+1∪…∪Cb+δ-2=T[b,b+δ-2],以T为定义集合的、码长为n的循环码C叫做Fq2上的设计距离为δ的BCH码。当n=q2m-1时C叫做q2-元本原BCH码,否则叫做非本原BCH码;如果b=1,C叫做狭义BCH码,否则叫做非狭义BCH码。 引理1 若gcd(n,q)=1,Fq2上的循环码C的定义集合为T,则C⊥h⊆C当且仅当T∩T-q=Φ,其中T-q={n-qt(modn)|t∈T}。 文献[12]将标准的CSS构造法推广到满足Hermite内积、迹Hermite内积和迹Euclide内积条件下的非对称量子码的构造中,给出了CSS-like(CSS-type)构造法,下述定理1.3就是构造满足Hermite对偶包含条件下的非对称量子码的CSS构造法。 在以前的工作中,人们利用q-元域上2个嵌套的满足Euclide对偶包含条件的BCH码构造非对称量子码,得到很多参数优良的非对称量子BCH码。然而利用q2-元域上满足Hermite对偶包含条件的BCH码构造非对称量子码,其构造结果大多局限于dz≤δmax,见文献[13]。为了突破这一局限,本节讨论m=2l+1和m=2l情况下,利用满足Hermite对偶包含条件的2个码长为n=22m-1的BCH码构造非对称量子码的参数,并且使所得到的dz>δmax。 2.1 当m=2l+1(l≥1)时非对称量子码的构造 u=min{x|x∈T-q},v=max{y|y∈T-q},与文献[19-21]相似,有如下引理1: 又因为 由此可知T⊥h至少包含u或者n-v-1个连续整数,因此δ(B⊥h)=max{u,n-v}。 下面定理3给出BCH码满足Hermite对偶包含的条件。 定理3 设n=22m-1,m=2l+1(l≥1)。 (3) 当1≤i≤l-1时,若δ1=22i+1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1-1,δ1<δ2≤24l-2i+2-1 或δ1=22i+1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=3·22i+1+1,δ1<δ2≤24l-2i+1-3, 证明 以(2)为例,令n=22m-1,m=2l+1(l≥1)。 同理可证(1)、(3)和(4)结论成立。 定理4 设n=22m-1,m=2l+1(l≥1)。 (1) 若i=0,当δ1=22i+1,δ1<δ2≤24l+1-1时,存在参数为[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非对称量子码; (2) 若1≤i≤l,当δ1=22i+1,δ1<δ2≤2·24l-2i+2-2 时,存在参数为[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非对称量子码; (3) 若1≤i≤l-1,当δ1=22i+1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1-1,δ1<δ2≤24l-2i+2-1 或δ1=22i+1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=3·22i+1+1,δ1<δ2≤24l-2i+1-3,存在参数为[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非对称量子码; (4) 若i≤l,当δ1=22i+1-2,δ1<δ2≤3·22l+1-1 或δ1=22i+1-1,δ1<δ2≤22l+2-1时,存在参数为[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非对称量子码。 证明 以(2)为例,设n=22m-1,m=2l+1(l≥1)。 同理可得(1)、(3)和(4)结论成立。 2.2 当m=2l(l≥2)时非对称量子码的构造 本节将构造一类码长为n=24l-1(l≥2)的非对称量子码的参数。和定理3类似,首先给出这些满足Hermite对偶包含条件的BCH码的最大设计距离,见定理4。 定理4 设n=22m-1,m=2l(l≥2)。 (1) 当i=1时, 若δ1=22i+1,δ1<δ2≤2·(24l-2-1) (2) 当2≤i≤l时, 若δ1=22i-1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=2·22i-2-1,δ1<δ2≤24l-2i+2-1 或δ1=22i-1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1,δ1<δ2≤2·(24l-2i-1) 根据CSS构造法和定理4的结论,可构造出当m=2l时另一类码长为n=22m-1(l≥2)非对称量子码的参数,见下列定理5。 定理5 设n=22m-1,m=2l(l≥2)。 (1) 若i=1,当δ1=22i+1,δ1<δ2≤2·(24l-2-1) 或δ1=22i-1-1,δ1<δ2≤24l-1-1时,存在参数为[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非对称量子码; (2) 若2≤i≤l,当δ1=22i-1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=2·22i-2-1,δ1<δ2≤24l-2i+2-1 或δ1=22i-1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1,δ1<δ2≤2·(24l-2i-1) 或δ1=3·22i-1+1,δ1<δ2≤24l-2i+1-3时,存在参数为[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非对称量子码。 说明1定理3和定理5构造出了两类非对称量子码的参数,然而需要说明的是,如果对于任何一个δ,将码的维数用公式形式表示出来是一件非常困难的事情,因此定理中用|T(δ)|表示定义集合的阶,用n-|T(δ)|表示码的维数。但是,当给定码长n以及dz、dx时,可以精确计算出非对称量子码的维数,在下节中将举例说明。 本节以m=3,4,5,6为例,将所得到的一部分码的参数与已有文献中的结果进行比较。下列表格中,记本文构造出的非对称量子码的参数为[[n,k,dz/dx]]4,文献[8,13]中非对称量子码的参数记为[[n,k′,dz′/dx′]]4。 表1 dz的最大下界与δmax的比较 表1给出了m分别为3,4,5,6时,我们构造出的非对称量子码的z-距离的最大下界和相应的δmax的比较,可以看出我们的z-距离远大于δmax。 表2 新的非对称量子码参数 表2给出m分别为3、4、5、6时,构造的新非对称量子码参数。需要说明当码长n=1 023时,表中给出非对称量子码参数[[1 023,543,dz≥125/dx≥5]]4,实际上,当dx≥5时,dz可以达到510,但是为了便于计算,我们仅列出dz≥125的情形。 表3 非对称量子码参数的比较 表3给出了当m=3,4,5,6时我们构造出的非对称量子码的参数和已有文献[8,13]中相关结论的比较。当码长为n=255,dz≥6/dx≥5时,我们构造出的码的维数为227,而文献[13]中给出的维数为225;我们构造出的参数为[[63,33,dz≥10/dx≥5]]4的非对称量子码,尽管维数和文献[8]中的相同,但是x-距离为5,而文献中的x-距离为4。 本文利用q2-元域上码长为n=22m-1的本原狭义BCH码构造两类非对称量子[[n,k,dz/dx]]4码的参数。首先,利用分圆陪集刻划2个嵌套的BCH码满足Hermite对偶包含的条件;其次,在m=2l+1(l≥1)和m=2l(l≥2)2种情况下,根据改进了的CSS构造法和满足Hermite对偶包含条件的2个BCH码构造出非对称量子码[[n,k,dz/dx]]4的参数;最后,将所构造出的一部分结果和已有文献中的结论进行比较,通过对参数的分析可以看出,我们得到的z-距离远大于δmax,除了得到一些新的码之外,还有一些码的参数优于已有文献中的结论,从而提高码的纠错能力。 [1] Shor P W. Scheme for Reducing Decoherence in Quantum Computer Memory[J]. Phys Rev A, 1995, 52: 2493-2496 [2] Steane A M. Error-Orrecting Codes in Quantum Theory[J]. Phys Rev Lett, 1996, 77: 793-797 [3] Aly S A. Asymmetric Quantum BCH Codes[C]∥IEEE International Conference on Computer Engineering and Systems, 2008: 157-162 [4] Calderbank A R, Rains E M, Shor P W, Sloane N J A. Quantum Error-Correction via Codes over GF(4)[J]. IEEE Trans on Information Theory, 1998, 44: 1369-1387 [5] Ioffe L, Mezard M M. Asymmetric Quantum Error-Correcting Codes[J]. Phys Rev A, 2007, 75: 032345 [6] Aly S A, Ashikhmin A. Nonbinary Quantum Cyclic and Subsystem Codes over Asymmetrically-Decohered Quantum Channels[C]∥2010 IEEE Information Theory Werkshop on, 2010: 6-8 [7] Aly S A. Quantum Error Control Codes[D]. Department of Computer Science, Texas A & M University, 2008 [8] Aly S A. Asymmetric Quantum BCH Codes[C]∥International Conference on Computer Engineering and Systems, 2008: 157-162 [9] Sarvepalli P K, Klappenecker A, Rotteler M. Asymmetric Quantum Codes: Constructions, Bounds and Performance[J]. Proc R Soc A, 2009, 465: 1645-1672 [10] Wang L, Feng K, Ling S, Xing C. Asymmetric Quantum Codes: Characterization and Constructions[J]. IEEE Trans on Information Theory, 2010, 56: 2938-2945 [11] Ezerman M F, Ling S, Sole P. Additive Asymmetric Quantum Codes[J]. IEEE Trans on Information Theory, 2011, 57: 5536-5550 [12] Ezerman M F, Ling S, Pasechnik D V. CSS-Like Constructions of Asymmetric Quantum Codes[J]. IEEE Trans on Inf Theory, 2013, 59: 6732-6754 [13] La Guardia G G. On the Construction of Asymmetric Quantum Codes[J]. Int J Theory Phys, 2014, 53: 2312-2322 [14] La Guardia G G. Asymmetric Quantum Codes: New Codes from Old[J]. Quantum Information Process, 2013, 12: 2771-2797 [15] La Guardia G G. New Families of Asymmetric Quantum BCH Codes[J]. Quantum Inform Computation, 2011, 11: 239-252 [16] Chen J Z, Li J P, Huang Y Y. Some Families of Asymmetric Quantum Codes and Quantum Convolutional Codes from Constacyclic Codes[J]. Linear Algebra and its Applications, 2015, 475: 186-199 [17] Huffman W C, Pless V. Fundamentals of Error-Correcting Codes[M]. Cambridge, U K: Cambridge University Press, 2003 [18] Macwilliams F J , Sloane N J A. The Theory of Error-Correcting Codes[M]. Amsterdam, the Netherlands: North-Holland, 1977 [19] Li R H, Xu G, Guo L B. On Two Promblems of Asymmetric Quantum Codes[J]. International Journal of Modern Physics Letter B, 2014, 28: 1450017-1450031 [20] Ma Y N, Feng X Y, Lv L D. Dual Containing BCH Codes and New Asymmetric Quantum Codes[C]∥5th International Conference on Instrumentation and Measurement, Computer, Communication, and Control, 2015: 1575-1578 [21] Ma Y N, Feng X Y, Xu G. New Asymmetric Quantum Codes overFq[J]. Quantum Information Process, 2016, 15: 2759-2769 Two Families of Dual Containing BCH Codes Ma Yuena1,2, Feng Xiaoyi1, Su Zhizhong3, Liu Yang2,3 1.School of Electronics and Information, Northwestern Polytechnical University, Xi′an 710072, China 2.School of Science, Air Force Engineering University, Xi′an 710051, China 3.The First Aeronautical College of Air Force, Xinyang 464000, China In this paper, we discuss the problem on the construction of asymmetric quantum codes from primitive narrow sense BCH codes. Take advantage ofq2-ary Hermite dual containing BCH code, we construct two families of new asymmetric quantum codes with much largerz-distance. Furthermore, the parameters of our asymmetric quantum codes presented here have better than the ones avaliable in the literature. asymmetric quantum code; BCH code; Hermite dual containing; CSS construction 2016-04-12 国家自然科学基金(11471011)与陕西省自然科学基金(2015JM1023)资助 马月娜(1977—),女,西北工业大学博士研究生,主要从事编码与密码、图像处理及模式识别研究。 O157.4 A 1000-2758(2016)05-0874-05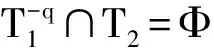

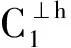
2 两类非对称量子纠错码的构造


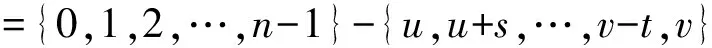
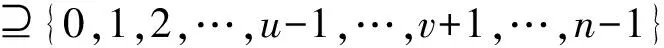
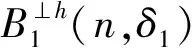
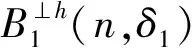
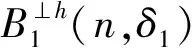
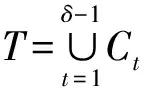
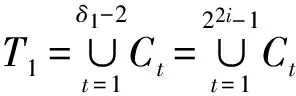
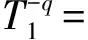
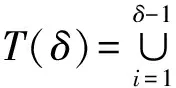
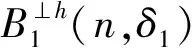
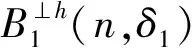
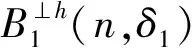
3 参数分析

4 结 论

