纵向数据下部分非线性模型的广义经验似然推断

肖燕婷,孙晓青,孙瑾

(西安理工大学理学院应用数学系,陕西西安710054)

纵向数据下部分非线性模型的广义经验似然推断

肖燕婷,孙晓青,孙瑾

(西安理工大学理学院应用数学系,陕西西安710054)

本文研究了纵向数据下部分非线性模型中未知参数的置信域的构造.利用经验似然方法,构造了非线性函数中未知参数的广义对数经验似然比统计量,证明了其渐近于卡方分布.同时,得到了未知参数的最大经验似然估计,并证明了其渐近正态性.

纵向数据;部分非线模型;经验似然;置信域

1　引言

纵向数据是生物医学、流行病学和计量经济学等学科中经常出现的一类复杂数据.由于其具有个体间观测值独立,个体内观测值相关的特性,不同于一般的独立数据,对其相关研究已成为统计学界的研究热点之一.

本文考虑如下的纵向数据下的部分非线性模型

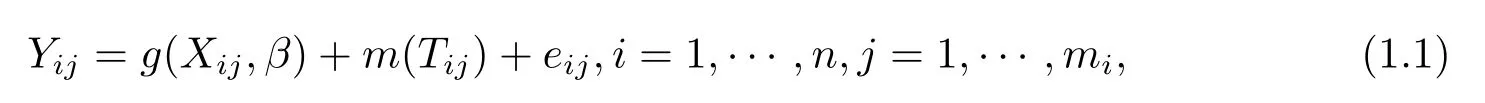
其中观测数据来自n个个体,第i个个体具有mi次观测,总的观测次数为和(Xij∈Rp,Tij)分别为第i个个体的第j(j=1,···,mi)次观测的响应变量和协变量;β为d×1维未知参数向量;g(.,.)为已知的可测函数;m(.)为定义在[0,1]上的未知光滑函数; eij为随机误差.记第i个个体的随机误差向量为ei=(ei1,ei2,···,eimi)T,{ei,i=1,···,n}相互独立,且E(ei)=0,Var(ei)=Σi并要求Σi为正定阵.

如果不考虑纵向数据,部分非线性模型(1.1)在独立数据下,已有不少学者研究了模型中未知参数和未知函数的估计,如Li和Nie[1]提出可以采用轮廓非线性最小二乘方法和局部线性逼近技术估计模型参数;Xiao等[2]将经验似然方法应用于该模型,构造了未知参数和未知函数的经验对数似然比统计量,从而可以得到未知参数的置信域和未知函数的同时置信带.

对于复杂数据下的部分非线性模型,冯三营等[3]考虑了当非参数协变量具有可加测量误差时,采用逆卷积方法,构造了模型中未知参数的经验对数似然比统计量,并证明了其具有渐近卡方分布.接着,文献[4]给出了模型中回归系数,光滑函数以及误差方差的最大经验似然估计.肖燕婷等[5]借助核实数据,给出了协变量带测量误差的部分非线性模型中未知参数的两种估计方法.武大勇等[6]在响应变量随机缺失的情形下,给出了未知参数的最大经验似然估计,并证明了估计的渐近正态性.刘强[7]在解释变量带有测量误差且响应变量随机缺失的复杂情形下,利用核实数据,给出了未知参数和非参数函数的两种估计.但在纵向数据下,对该模型的研究还比较少.

本文针对纵向数据下的部分非线性模型(1.1),利用Owen[8]等提出的经验似然方法,构造了模型中未知参数β的广义对数经验似然比统计量,证明了所提统计量的渐近χ2分布,所得结果可以构造未知参数的置信域.同时,利用对数经验似然比函数,得到了未知参数的最大经验似然估计,证明了其渐近正态性.

2　方法与主要结果

假设观测数据{(Xij,Tij,Yij),i=1,···,n,j=1,···,mi}由模型(1.1)产生.对(1.1)式两边在给定Tij=t时求条件期望,可以得到

其中m1(t,β)=E(g(Xij,β)|Tij=t),m2(t)=E(Yij|Tij=t).利用核估计方法,可以得到m1(t,β)和m2(t)的估计,分别由下式给出

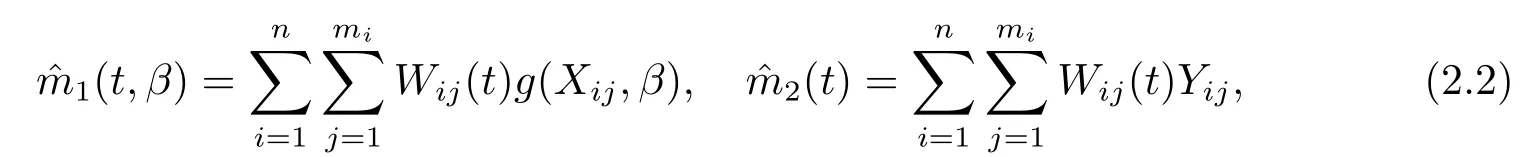
其中Wij(t)=Kh(Tkl-t)为核权函数,Kh(.)=K(./h)且K(.)为核函数,h为带宽.因此m(t)的估计为

为了构造未知参数β的对数经验似然比函数,需要引入如下的辅助随机向量

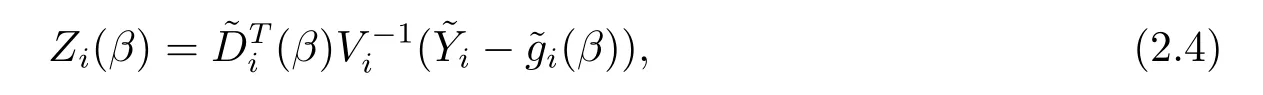
其中Vi可以为任意指定的工作协方差阵.但在实际应用中,为了避免由于错误指定协方差阵而引起的估计效率的降低,可以用其估计值代替真实值Vi,且,其中Zi(β)=0,且在Zi(β)中令Vi=I得到的未知参数β的初估计.

类似于文献[9],定义如下广义的经验对数似然比函数

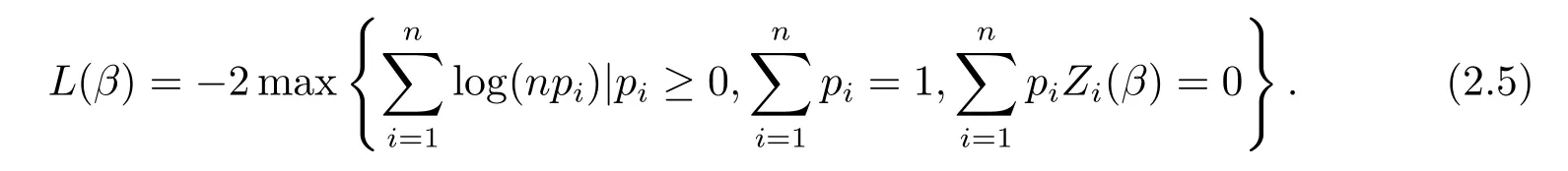
根据Lagrange乘子方法,L(β)可以写成

其中λ=λ(β)由下式决定

通过极小化L(β),可以得到参数β的最大经验似然估计,记做.将代入(2.3)式,可以得到未知函数m(t)的最终估计,为(t)=2(t)-1(t,).

3　渐近性质

令g(1)(Xij,β)=h(Tij,β)+uij(β),i=1,···,n,j=1,···,mi,其中h(Tij,β)= E(g(1)(Xij,β)|Tij),且E(uij(β))=0.令ha(Tij,β)为h(Tij,β)的第a个分量,a=1,···,d.类似于(2.2)式,ha(t,β)的核估计可以定义为a(t,β)=其中(Xij,β)为g(1)(Xij,β)的第a个分量.

为了得到估计量的渐近性质,需要给出以下假设条件.

C1:带宽满足h=h0N-1/5,对某个h0＞0.

C2:核函数K(.)为对称的概率密度函数,且在它的支撑[-1,1]上有界.

C4:T的密度函数f(t)在(0,1)是连续可微的,且有界.

C5:对任意的β,非线性函数g(x,β)具有二阶连续导数.

C6:函数m(t),ha(t,β),a=1,···,d在(0,1)上是二次连续可微的.

C7:定理2.2中的矩阵Γ为正定矩阵.

注条件C1-C7是文献中经常用到的条件.条件C1说明了在估计m(.)时不必欠光滑; C2为核函数的一般性条件;条件C3-C6为部分非线性模型中常见的条件;条件C7保证了最大经验似然估计的渐近方差的存在.

定理2.1假设条件C1-C6成立,如果β为真实参数值,则有

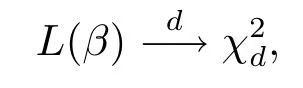
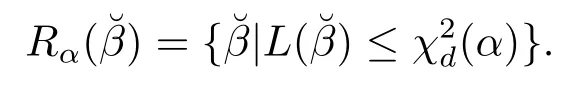
定理2.2假设条件C1-C7成立,则有

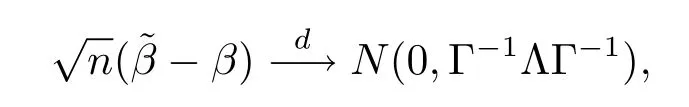
4　定理的证明

为了完成定理的证明,需要首先给出以下引理.

引理1假设条件C1-C6成立,则有

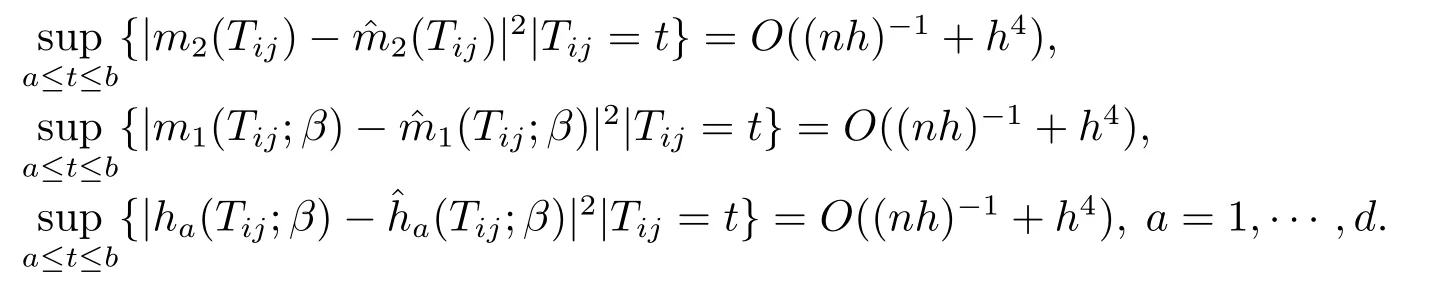
证仅给出以上第1个等式的证明,其余两个等式可用同样的方法证明.根据不等式(A+B)2≤2A2+2B2可以得到

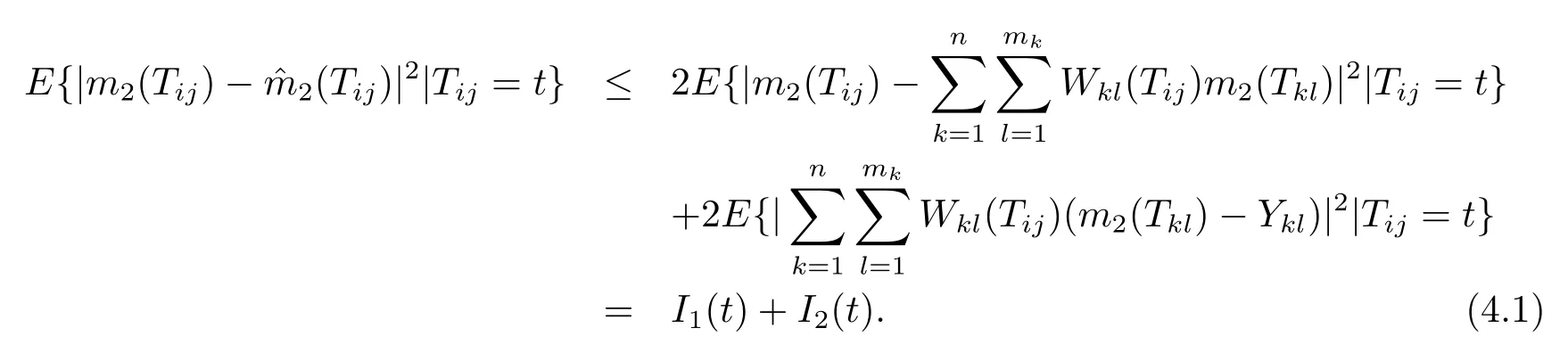
类似于文献[10]中引理1中的证明,可以得到

基于这样的事实E[Ykl-m2(Tkl)]=0,由条件C2-C4可得

结合(4.1)-(4.3)式,该结论得证.

引理2假设条件C1-C7成立,如果β为参数的真值,则有

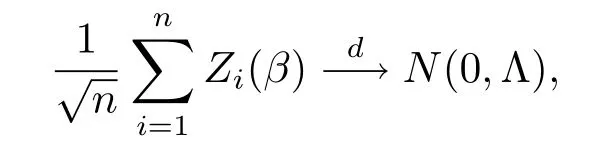
其中Λ的定义见定理2.2.

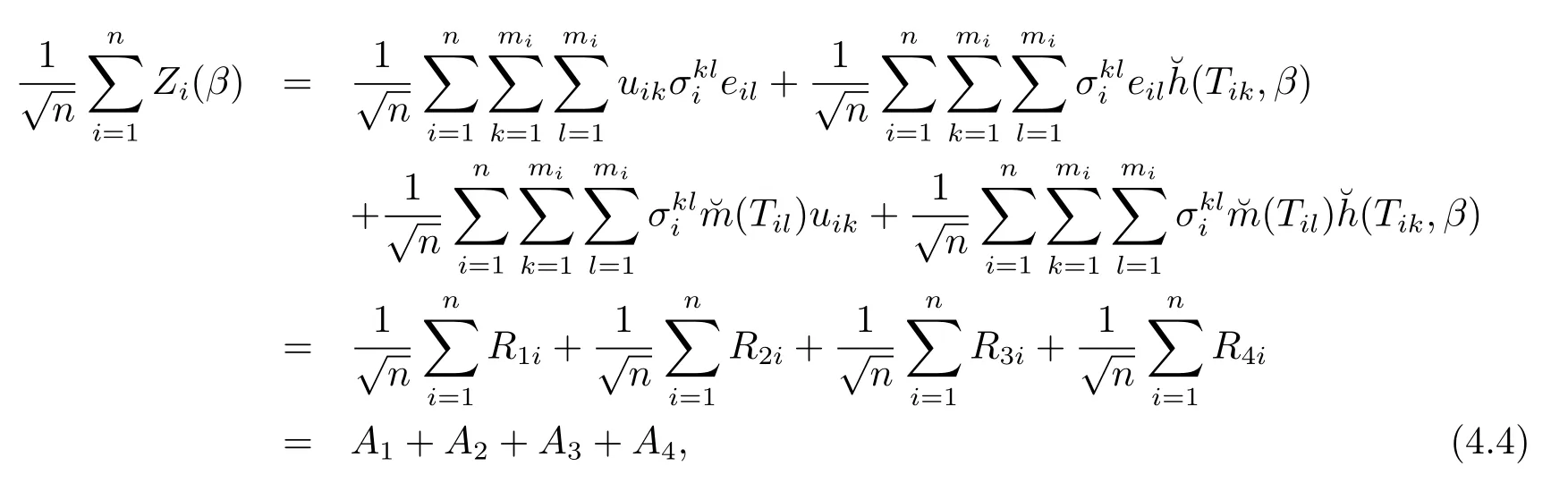
对A1,很容易得到E(A1)=0和cov(A1)=Λ.根据Lindeberg-Feller中心极限定理可以得到

根据引理1可以得到E||A2||2≤c{(nh)-1+h4}→0,因此得到类似的还有E||A3||2≤c{(nh)-1+h4}→0,即进一步,根据引理1和Cauchy-Schwarz不等式,可以得到→0,由此推得

综合以上讨论,这就完成了该引理的证明.

引理3假设条件C1-C7成立,如果β为参数的真值,则有

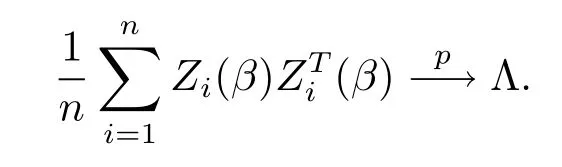
证仍然使用引理2中的记号,并记Ji=R2i+R3i+R4i,则有

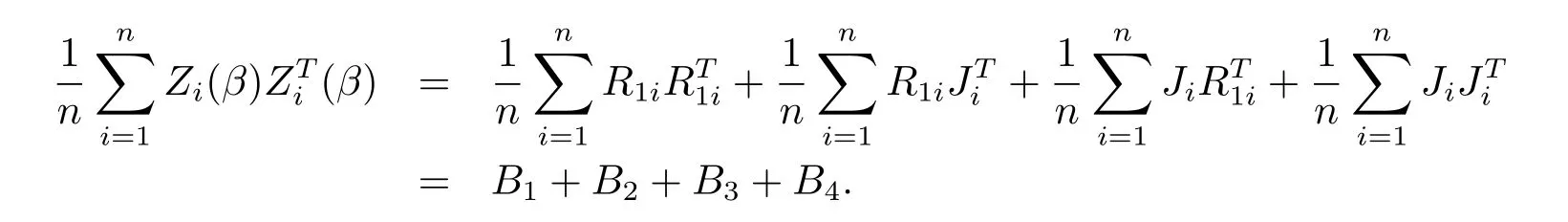
定理1的证明根据引理2-3和Owen[8]的思想,可以得到

对(2.6)式作用Taylor展式,并采用引理2-3,可以得到

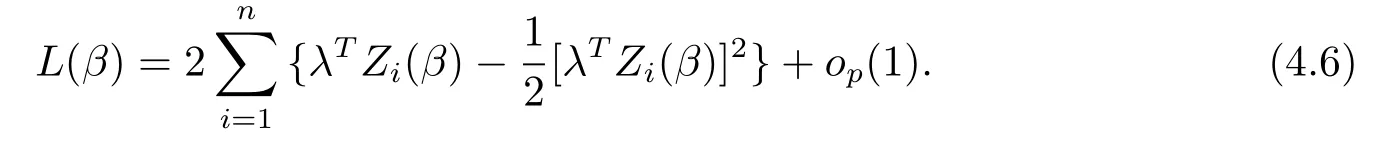
根据引理2和(4.5)式,(4.6)式,可以得到

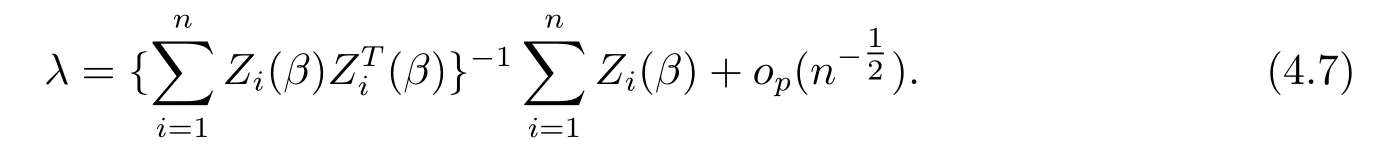
将(4.7)式代入(4.6)式,可以得到

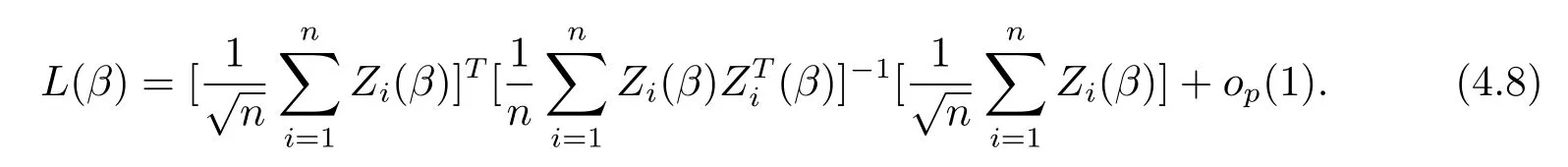
再结合(4.8)式,引理2-3,该定理得证.

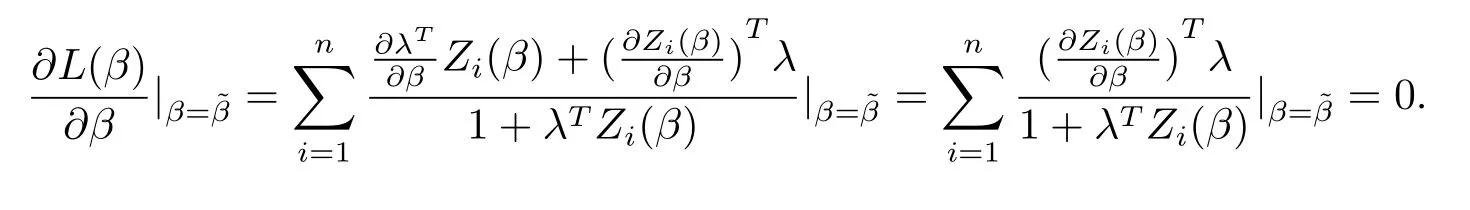
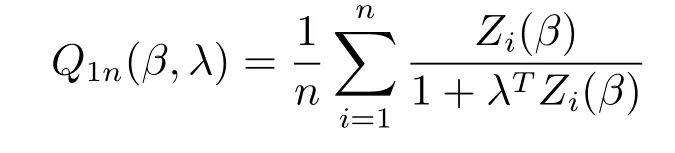
和

对Q1n(,)和Q2n(,)在点(β,0)作用Taylor展式,可以得到

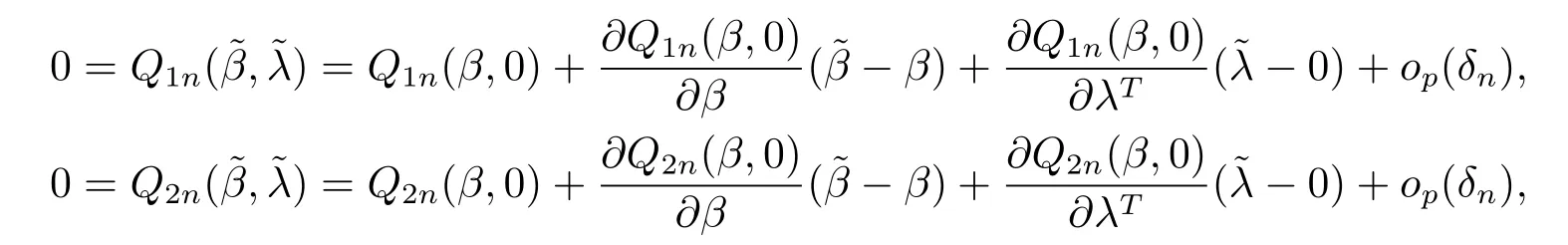
其中δn=||-β||+||||,因此可以得到

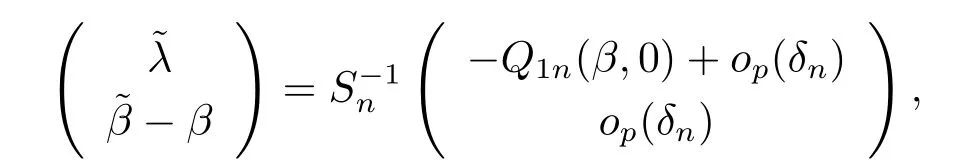
其中Sn=

根据(4.5)式并注意到Q1n(β,0)=Zi(β)=Op(n-1/2)可以得到δn=op(n-1/2).经过简单计算可以得到

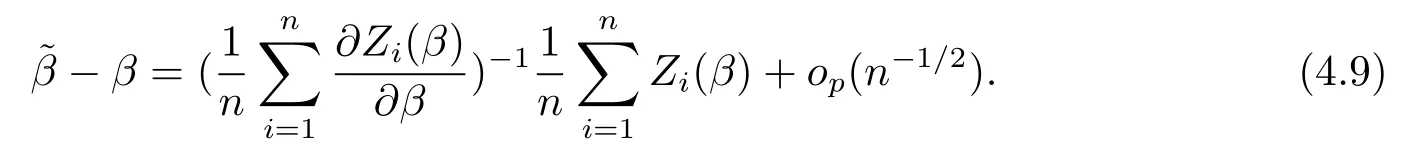
根据引理1可以证明

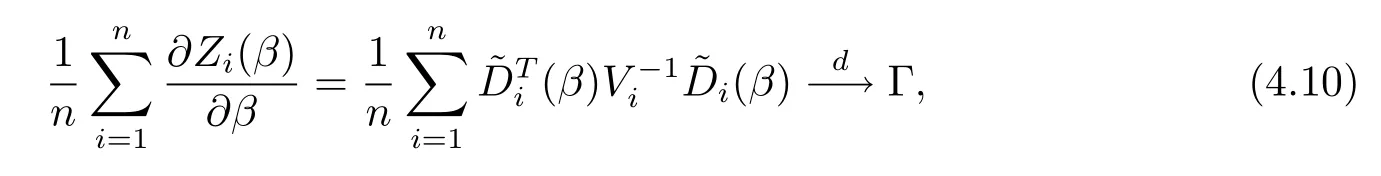
此式连同(4.9)式及引理2和Slutsky定理,可以证得该定理.

[1]Li R,Nie L.Efficient statistical inference procedures for partially nonlinear models and their applications[J].Biometrics,2008,64(3):904-911.

[2]Xiao Y T,Tian Z,Li F X.Empirical likelihood-based inference for parameter and nonparametric function in partially nonlinear models[J].J.Korean Stat.Soc.,2014,43(4):367-379.

[3]冯三营,李高荣,薛留根,陈放.非线性半参数EV模型的经验似然置信域[J].高校应用数学学报,2010, 25(1):53-63.

[4]冯三营,薛留根.非线性半参数EV模型的最大经验似然估计[J].数学物理学报,2012,32(4):729-743.

[5]肖燕婷,田铮,孙瑾.核实数据下非线性半参数EV模型的估计[J].数学杂志,2015,35(5):1075-1085.

[6]武大勇,李锋.随机缺失下半参数回归模型的最大经验似然估计[J].山东大学学报,2015,50(4):20-23.

[7]刘强.缺失数据下非线性半参数EV模型的估计[J].系统科学与数学,2010,30(9):1236-1250.

[8]Owen A.Empirical likelihood ratio confidence intervals for a single function[J].Biometrika,1988, 75(2):237-249.

[9]Li G R,Tian P,Xue L G.Generalized empirical likelihood inference in semiparametric regression model for longtitudianl data[J].Acta Math.Sinica,Engl.Ser.,2008,24(12):2029-2040.

[10]薛留根,朱力行.纵向数据下部分线性模型的经验似然推断[J].中国科学,2007,37(1):31-44.

2010 MR Subject Classification:62G05

GENERALIZED EMPIRICAL LIKELIHOOD INFERENCE FOR PARTIALLY NONLINEAR MODELS WITH LONGITUDINAL DATA

XIAO Yan-ting,SUN Xiao-qing,SUN Jin
(Department of Applied Mathematics,Xi’an University of Technology,Xi’an 710054,China)

In this paper,we study the construction of confidence region for unknown parameter in partially nonlinear models with longitudinal data.By empirical likelihood method, the generalized empirical log-likelihood ratio for parameter in nonlinear function is proposed and shown to be asymptotically chi-square distribution.At the same time,the maximum empirical likelihood estimator of the parameter in nonlinear function is obtained and asymptotic normality is proved.

longitudinal data;partially nonlinear models;empirical likelihood;confidence region

MR(2010)主题分类号:62G05O212.7

A

0255-7797(2016)06-1238-07

∗2015-10-23接收日期:2016-02-25

国家自然科学基金(61303223;11501443);陕西省自然科学基金(2015JM1039);陕西省教育厅基金(2016JK1545);西安理工大学校基金(2015CX009

肖燕婷(1981-),女,陕西西安,讲师,主要研究方向:非(半)参数统计.