修正HS共轭梯度法在大规模信号重构问题中的应用

陈凤华,李双安

(郑州工商学院公共基础教学部,河南郑州451400)

修正HS共轭梯度法在大规模信号重构问题中的应用

陈凤华,李双安

(郑州工商学院公共基础教学部,河南郑州451400)

本文研究了压缩感知在大规模信号恢复问题中应用的问题.利用修正HS共轭梯度法及光滑化方法,获得了具有较好重构效果的算法.数值实验表明用修正HS共轭梯度法解决大规模信号恢复问题是可行的.

压缩感知;修正HS共轭梯度法;稀疏信号;Nesterov光滑技术

1　引言

在压缩感知问题中,若先验知道原信号在某个变换下是可压缩的(或是稀疏的),则可以通过如下一个最小ℓ0范数问题恢复信号

这里ℓ0范数表示向量非零元素的个数.但是求解最小ℓ0范数问题是一个NP难问题,即最小ℓ0范数问题的求解需要列举原信号中非零值的所有排列组合情况,计算量巨大,相关研究见文献[1].

此后,人们转而求解最小ℓ1范数问题,而且证明了在一定的条件下,最小ℓ1范数问题和最小ℓ0范数问题的解是等价的,见文献[2].因此问题(1.1)转化为求解下面的最小ℓ1范数问题

最小ℓ1范数问题的求解是一个凸优化问题,这个问题能够转化为线性规划问题,见文献[3,4].然而在实际中求解线性规划问题(1.2)是很难的.在压缩感知问题中,当矩阵A是大且稠密的,线性规划问题(1.2)常常是病态的.设矩阵A是行满秩的,问题(1.2)可转化为ℓ1正则化最小二乘问题(见文献[5])

这里λ是正则化参数.

2　算法

因为‖u‖1是关于u的非光滑凸函数,所以对于问题(1.3),次梯度基本方法的效果可能很差.本文通过求解问题(1.3)的一个适当的光滑形式,来求解ℓ1最小化问题(1.2).

由文献[6],利用Nesterov光滑技术,光滑化‖u‖1为如下光滑函数

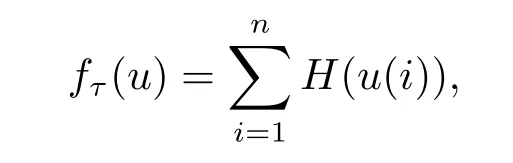
其中

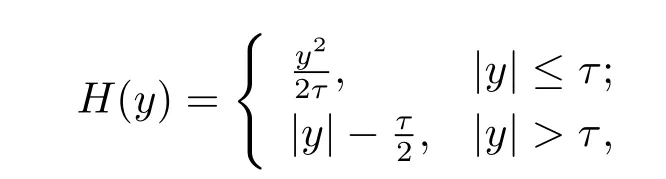
光滑函数fτ(u)是凸的,梯度∇fτ(u)是Lipchitz连续的,且其分量为

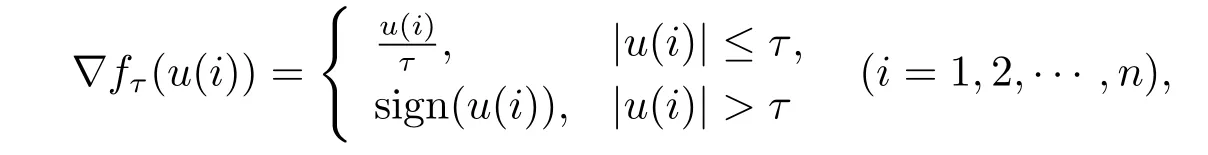
其中

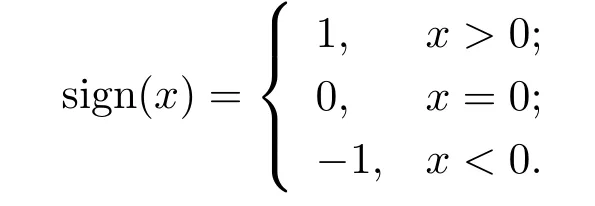
令F(u)=λfτ(u)+则问题(1.3)转化为如下无约束光滑凸规划问题

F(u)是可微的,其梯度∇F(u)=λ∇fτ(u)+AT(Au-b)是Lipchitz连续的.为方便,记gk=∇F(uk),yk=∇F(uk+1)-∇F(uk)=gk+1-gk.

求解问题(2.1),共轭梯度法的迭代公式如下

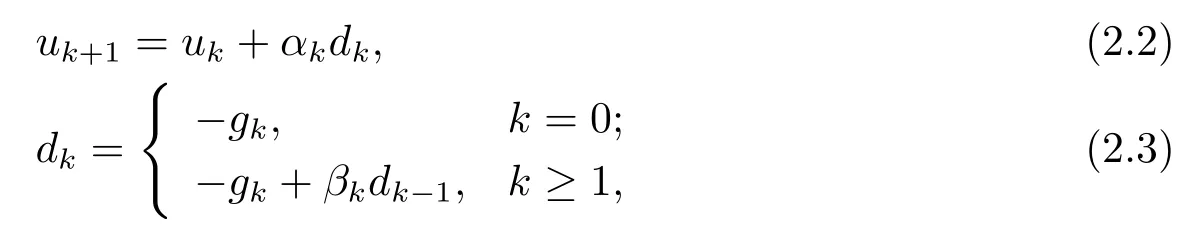
其中αk为搜索步长,dk为搜索方向,βk为参数.

共轭梯度法的关键是参数βk的选取,常用的βk公式有如下几种

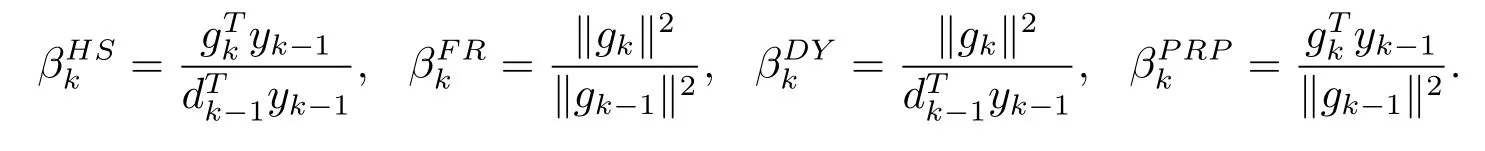
一些文献对βk的构造及算法的收敛性做了大量的研究,见文献[7,8].文献[8]指出, PRP,HS方法在数值计算中有很好的表现,但是即使使用精确线搜索PRP方法也不会有全局收敛性.FR,DY方法则具有较好的收敛性质.为寻求兼具良好收敛性和优秀数值结果的算法,许多研究者在经典共轭梯度法的基础上推出新的βk公式.

本文我们提出用修正HS共轭梯度法解决大规模信号恢复问题(2.1),且在适当的假设条件下证明了本文提出的算法具有全局收敛性,最后数值实验结果表明用修正HS共轭梯度法解决大规模信号恢复问题是可行的．

本文构造如下搜索方向

其中

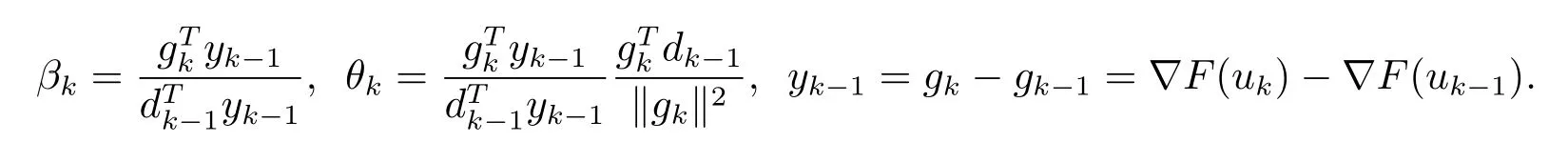
引理2.1对任一线搜索,搜索方向由(2.4)式定义,则有

证由(2.4)式,有

算法2.1问题(2.1)的修正HS共轭梯度算法:

步骤0给定初始点u0∈Rn,终止误差0≤∈≪1,τ0=0.6,0＜ρ1＜ρ2＜1,令k:=0;

步骤1计算gk=∇F(uk),若‖gk‖＜∈,且光滑参数τk≤∈,算法停止;否则,转下一步;

步骤2计算搜索方向dk,搜索方向由(2.4)式定义;

步骤3计算步长αk:

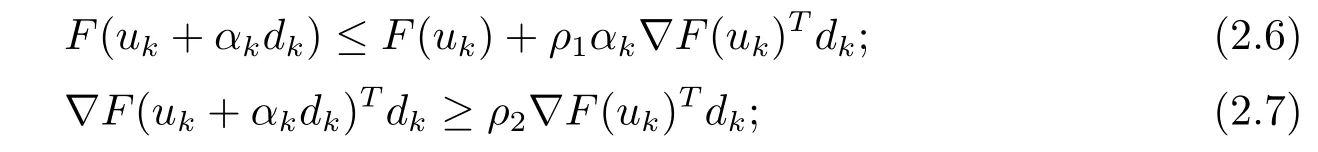
步骤4更新:令uk+1=uk+αkdk,更新光滑参数

步骤5循环:置k:=k+1,转步骤1.

3　全局收敛性

本文提出用修正HS共轭梯度法解决大规模信号恢复问题(2.1),且在适当的假设条件下证明了本文提出的算法具有全局收敛性.

为证明算法2.1具有全局收敛性,先作如下基本假设.

H1水平集Ω={x∈Rn|F(x)≤F(x0)}有界.

H2在Ω的某邻域N内,F(x)连续可微,且其梯度∇F(x)=g(x)是Lipschitz连续的,即存在一常数L＞0使得

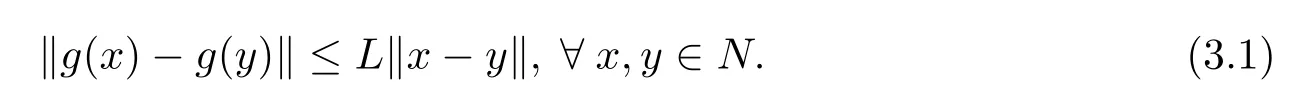
由假设H1、H2知,存在一常数M＞0满足

[8,9],有如下两个引理.

引理3.1[9]若假设条件H1、H2成立,则算法是良定的.

注由(2.6)式知目标函数值序列{F(xk)}是一下降序列,有＜+∞,结合(3.2)式有

引理3.2[8]若假设条件H1、H2成立,对任一共轭梯度法的迭代形式(2.2),其中dk满足＜0且αk满足条件(2.6)和(2.7),则

式(3.4)结合式(2.5)有

定理3.3如果假设条件H1、H2成立,算法2.1产生的迭代序列为{uk},若存在常数r＞0满足

证由(2.4)式定义的dk及式(3.1)、(3.2)、(3.6)有

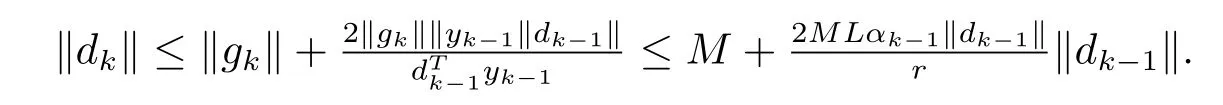
由(3.3)式知存在一常数t∈(0,1),存在一正整数k,使得当k≥k0有

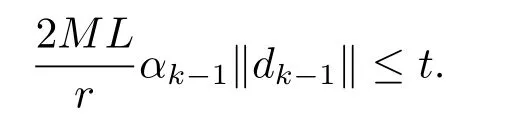
因此∀k＞k0有

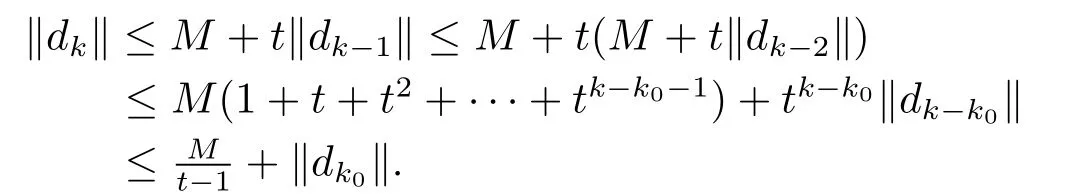
式(3.5)结合式(3.7)有

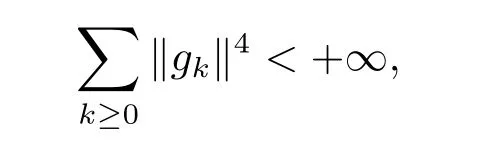
在压缩感知理论中,当{min‖u‖1:Au=b}有唯一解时,精确恢复才会实现.参考文献[5],有下面的定理.

定理3.4设ℓ1范数最小化问题min{‖u‖1:Au=b}有唯一最优解,算法2.1产生的迭代序列为{uk},当‖u‖1的光滑参数τk→0时,则=u∗,这里u∗=argmin{‖u‖1: Au=b}.

证记第k步的目标函数Fk(u)的最小值点为即

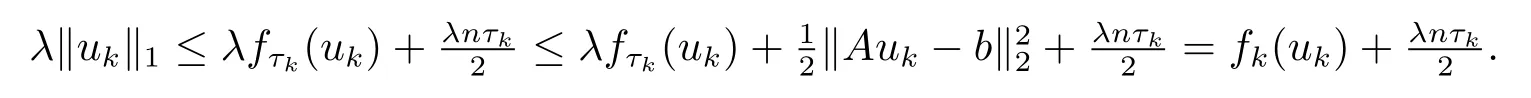
因为Fk(u)是凸函数,有Lipschitz连续梯度,由文献[5]引理2.3有,Lipschitz常数满足

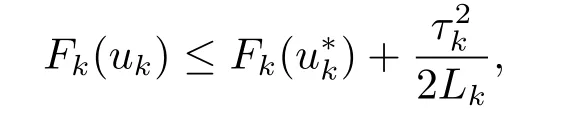
所以

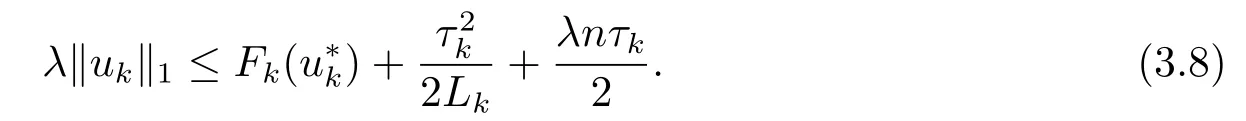
故当光滑参数τk→0时,(3.8)式表明序列{uk}有极限点.令u∗表示这个序列的任意极限点,由文献[5]结合定理3.3,可证u∗是可行点,且是问题(1.2)的KKT点.又问题(1.2)是凸规划问题,故u∗是问题(1.2)的最优解.

4　数值实验

实验中,参数选取ρ1=0.2,ρ2=0.7,误差精度∈=10-8.A为m×n维随机矩阵,uexact表示n维k稀疏原信号,满足Auexact=b,u表示本文算法恢复出来的信号,相对残差相对误差图1和图2中的圈和点分别表示原信号和经由我们的算法恢复出来的信号.

表1、图1选取A的维数都是512×1024,表2对应的正则化参数λ=0.1,图2选取A的维数分别是256×512,512×1024,1024×2048,2048×4096.

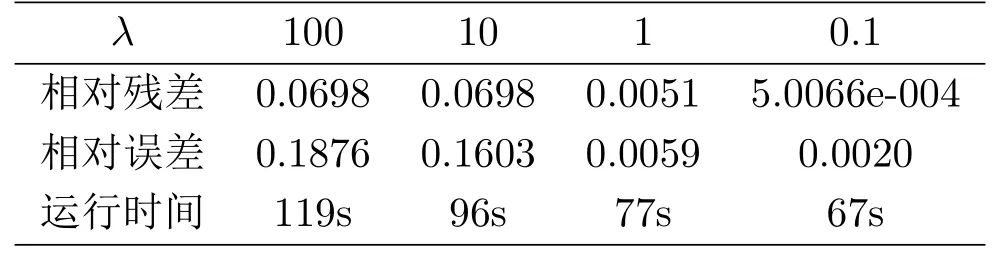
表4.1:λ按递减规则产生的数值结果

表4.2:信号维数按递增规则产生的数值结果

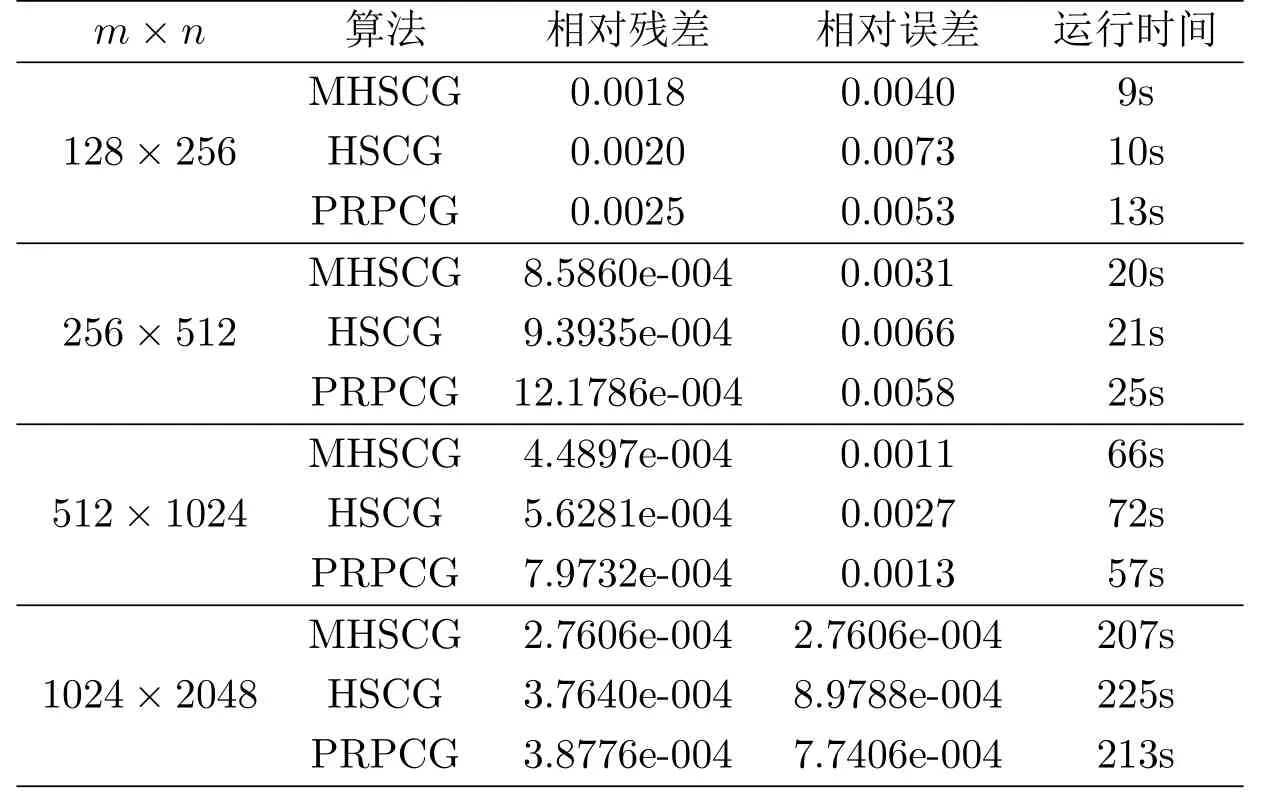
表4　.3:信号维数按递增规则产生的数值结果

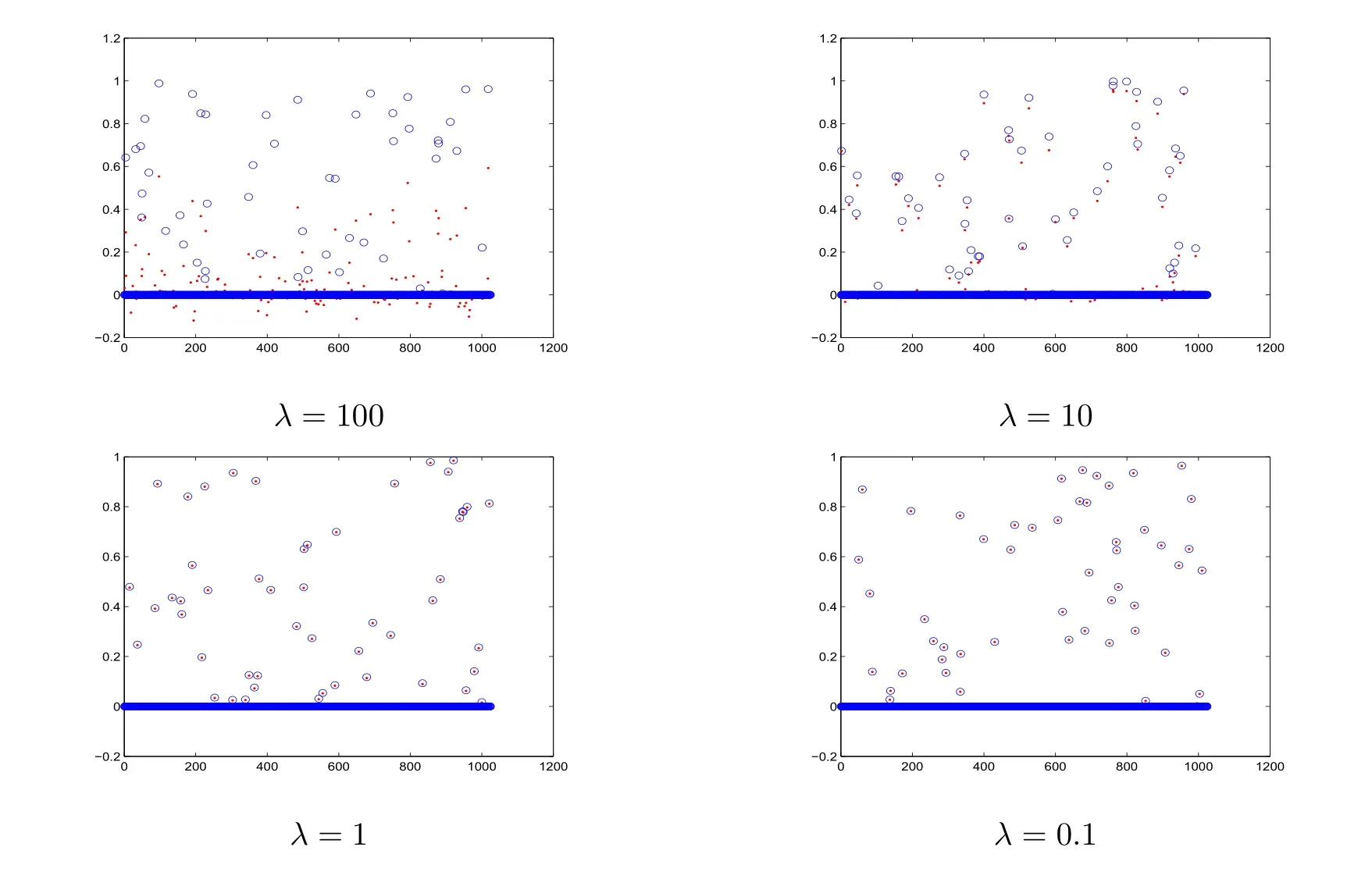
图4.1:四幅图分别表示λ不同取值下的信号恢复效果图

5　结论

本文提出用基于Nesterov光滑技术和修正HS共轭梯度法的压缩感知重构算法解决大规模信号恢复问题,最后做了两类数值实验,第一类反映了随着正则化参数λ的变化,相对残差、相对误差、运行时间的变化,以及随着原信号的维数的变化,相对残差、相对误差、运行时间的变化;第二类实验用本文提出的修正HS共轭梯度法与HS共轭梯度法、PRP共轭梯度法解决大规模信号恢复问题作对比,实验结果表明用修正HS共轭梯度法解决大规模信号恢复问题是可行的.该算法在图像处理中有直接的应用价值.相关研究见文献[10,11].

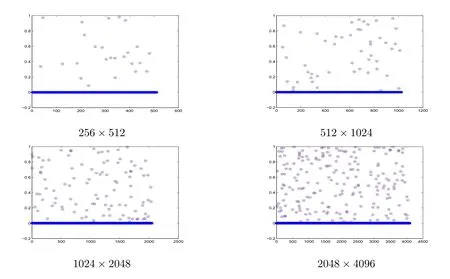
图4.2:四幅图分别表示信号维数不同取值下的信号恢复效果图

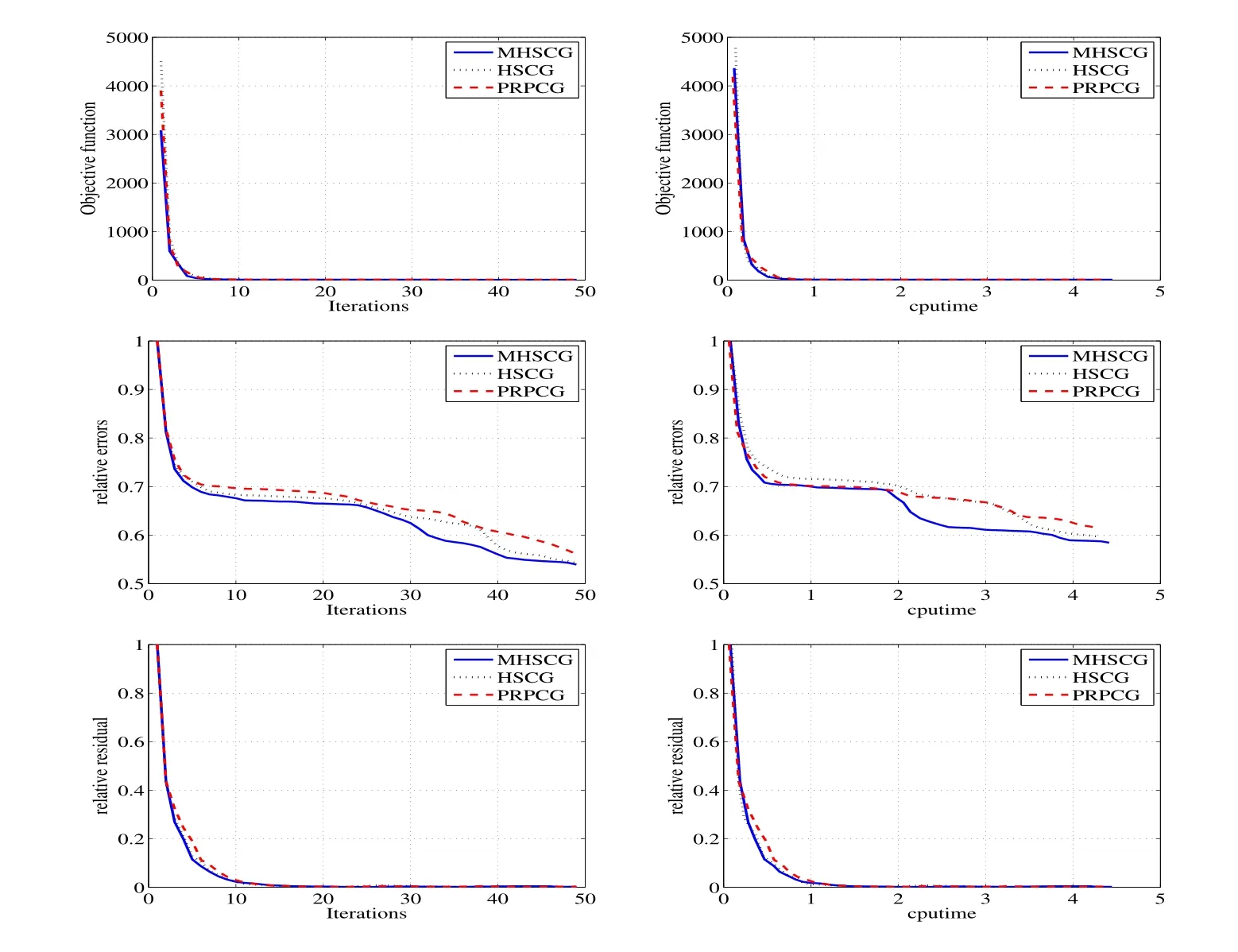
图4.3:修正HS共轭梯度法(图中标为MHSCG)与HS共轭梯度法(图中标为HSCG)、PRP共轭梯度法(图中标为PRPCG)作比较,上图分别反映了目标函数值、相对误差、相对残差随迭代步、运行时间的变化.

[1]Zhu H,Xiao Y,Wu S Y.Large sparse signal recovery by conjugate gradient algorithm based on smoothing technique[J].Comp.Math.Appl.,2013,66(1):24-32.

[2]Donoho D L.For most large underdetermined systems of linear equations the minimal 1-norm solution is also the sparsest solution[J].Commun.Pure Appl.Math.,2006,59(6):797-829.

[3]Candes E J,Tao T.Near Optimal Signal Recovery From Random Projections And Universal Encoding Strategies[J].IEEE Trans.Inform.The.,2007,52(12):5406-5425.

[4]Donoho L D.Compressed sensing[J].IEEE Trans.Inform.The.,2006,52(4):1289-1306.

[5]Aybat S N,Iyengar G.A first-order smoothed penalty method for compressed sensing[J].SIAM J. Optim.,2011,21(1):287-313.

[6]Nesterov Y.Smooth minimization of non-smooth functions[J].Math.Prog.,2005,103(1):127-152.

[7]Al Baali M.Descent property and global convergence of the Fletcher-Reeves method with inexact line search[J].IMA J.Numer.Anal.,1985,5(1):121-124.

[8]Ioannis E,Livieris,Panagiotis Pintelas.Globally convergent modified Perry’s conjugate gradient method[J].Appl.Math.Comp.,2012,218(18):9197-9207.

[9]Zhang L,Zhou W,Li D H.A descent modified Polak-Ribiere-Polyak conjugate gradient method and its global convergence[J].Ima.J.Numer.Anal.,2006,26(4):629-640.

[10]陈凤华,李双安.BFGS校正拟牛顿法解决大规模信号恢复问题[J].数学杂志,2015,35(3):727-734.

[11]房明磊,朱志斌.互补约束规划问题的一个广义梯度投影法[J].数学杂志,2011,31(4):685-694.

2010 MR Subject Classification:90C05;65K05

THE APPLICATION OF A MODIFIED HS CONJUGATE GRADIENT METHOD FOR LARGE-SCALE SIGNAL RECONSTRUCTION PROBLEM

CHEN Feng-hua,LI Shuang-an
(Teaching Department of the Public Infrastructure,Zhengzhou Technology and Business University, Zhengzhou 451400,China)

In this paper we study application about the compressed sensing in large-scale signal recovery problem.By the modified HS conjugate gradient method and smoothing technique, the algorithm which possesses better reconstruction effect is obtained.Preliminary numerical results show that our algorithm is suitable for solving large-scale sparse signal recovery problems.

compressed sensing;modified HS conjugate gradient method;sparse signal; Nesterov’s smoothing technique

MR(2010)主题分类号:90C05;65K05O221.1

A

0255-7797(2016)06-1291-08

∗2015-12-16接收日期:2016-04-15

国家自然科学基金(11061011;11361018);河南省高等学校重点科研项目(17A110032);河南省教育厅科学技术研究重点项目(12B110011).

陈凤华(1982-),女,湖北仙桃,讲师,主要研究方向:优化理论与算法研究.