时延情形下的分布式随机无梯度优化算法

任芳芳+李德权

摘要：由于多个体系统在信息交流的过程中存在通信时延，系统会出现接收信息滞后的情况，从而影响优化算法的收敛速度。为了解决时延对优化算法产生的影响， 提出了时延情形下的多个体系统分布式随机无梯度优化算法。假定系统中每个个体仅知道其自身的局部目标函数，利用系统中个体间交互时延信息来寻求这些局部目标函数之和的最小值， 通过系统扩维将有时延的优化问题转化为无时延的优化问题。由于个体的局部目标函数有可能非凸故其次梯度不一定存在或很难计算，因而采用分布式随机无梯度方法。理论分析表明只要个体间的通信时延有上界，所提算法依然收敛。

关键词：多个体系统；分布式优化；随机无梯度；通信时延

中图分类号：TP13 文献标志码：A文章编号：1672-1098（2016）01-0034-06

Abstract：Considering the delay of information communication among agents， which affect the convergence speed of the algorithm， the randomized gradient-free method for multi-agent optimization with communication delay was proposed， where its assumed that every agent only knows its own local objective function. The optimization goal is to minimize a sum of local objective functions through the interaction of delay information among agents in the system. Firstly， the optimization problem with delay was converted into the optimization problem without delay through augmenting delay nodes. Because the local objective function of agent is likely to be nonconvex， its subgradient does not exist or it is hard to be calculated， the distributed randomized gradient-free method was used. The theoretical analysis showed that the proposed algorithm is still convergent if the communication delays are upper bounded.

Key words：multi-agent system； distributed optimization； randomized gradient-free， communication delay

近年来，多个体分布式凸优化问题及其优化算法引起了人们的广泛关注，而多个体分布式优化算法是在集总式算法的基础上发展起来的。所谓集总式算法是指在多个体系统中，不是所有个体都发挥同样的作用，只有某个个体处于中心地位，负责处理其他个体的数据，并将数据反馈给其他个体。和集总式算法不同，分布式算法则是指多个体系统中的每个个体都对应着一个局部凸目标函数，并且个体之间进行信息交流，最终求得凸目标函数的最小值。和以往的集总式算法相比，分布式算法有很多优点，尤其在许多大规模的优化问题中占有很大优势，并且在生物工程、人工智能等许多领域有广泛应用，因此研究多个体的分布式优化算法有很大的意义。

随着计算机的广泛应用，人们进入了大数据云计算的时代，因此对多个体分布式优化的研究也越来越深入。但这些方法主要是标准次梯度和一致性算法的结合。标准次梯度算法是将总的最优化任务分解，同时每个个体需要将自身的信息与周围邻居个体的信息进行加权组合，再根据自身的次梯度信息进行最优化，经过一系列的迭代运算，使得所有个体的状态都达到一致。事实上，一致性算法也是广泛研究的一个课题，即个体间通过信息交流使所有个体的状态最终达到一致并使结果达到最优。文献[1]最早给出了标准次梯度方法并分析了其收敛性。文献[2]922介绍了约束一致性和优化算法。在此基础上，文献[3]则介绍了基于随机投影的次梯度算法，文献[4]1715给出一种基于一致性算法的原始对偶次梯度方法。在文献[4]1720的启发下，文献[5-6]提出了一种分布式对偶平均算法（DDA）以及基于Push-sum的DDA算法。上述研究都是适用于多个体系统中的每个个体对应的局部目标函数存在凸函数且次梯度的情况。而文献[7-8]研究的是个体的局部目标函数是非凸的、次梯度不存在或很难计算的情况，因此文献[9]提出了一种分布式随机无梯度优化算法。

然而，以上都是假设在任何时刻每个个体都可以即时的和周围个体之间进行信息交流。而在文献[10-12]1108中，由于有限的带宽，随机的传输延迟以及不确定的连接拓扑，个体之间的信息交流可能出现延时的情况。为此，文献[12]1139给出了时延情形下的分布式次梯度优化算法以及具有通信时延的二阶系统一致性。

本文主要研究时延情形下的分布式随机无梯度优化算法。

1符号说明

网络中个体间的信息通信通常可以建模成一个有向图G（k）=（V，E（k），P（k）），其中V=（1，2，…，n）表示个体集合，n表示个体数目，E=（e1，e2，…，en）表示边集，P（k）表示网络拓扑图G在k时刻的权重邻接矩阵，并且G是一个有向图[13]。令Rn为一个n维向量空间，‖x‖为向量x的欧几里得范数，ΠX[x]表示向量x到集合X上的欧几里得投影，[x]i表示向量x的第i个分量，xT表示向量x的转置，[P]ij代表矩阵P的第i行j列的元素，E[x]代表向量x的期望值。f（x）则表示函数f（x）在x处的梯度。

2问题描述

考虑如下由n个个体组成的多个体系统分布式凸优化问题：

minx∈Rmh（x）=∑ni=1hi（x） （1）

这里h（x）为目标函数，x∈Rm是一个全局决策向量，hi∶Rm→R是个体i（i∈V）的自身目标函数并仅为个体i知道，同时假设其是Lipschitz连续的且Lipschitz常数为G0（hi），XRm是非空闭凸集。式（1）表明整个系统的目标函数可以分解成系统中各个个体自身目标函数之和。

考虑每个hi不一定是光滑的且可能是非凸函数。因此其次梯度不存在或很难计算。故已有相关基于次梯度的分布式优化算法对本文不再适用。为此，用一个高斯函数hiμi 来近似代替hi，此时式（1）的光滑版本如下：

minx∈Xhu（x）=∑ni=1hiui （x） （2）

这里hiui （x）是hi（x）的高斯近似[7]1116且满足：

hiui （x）=1ω∫Rmhi（x+μiξ）e-12‖ξ‖2dξ （3）

这里ω=∫Rme-12‖ξ‖2dξ=（2π）m2，μi代表函数fiμi 的光滑系数，是一个非负标量，ξ是随机向量。

3算法介绍

31DRGF法

在实际情况中，由于多个体在信息交流的过程中存在通信时延，为此提出如下的时变时延情形下的分布式随机无梯度优化算法（DRGF法）。

1） 初始化

① 选择一个随机向量xi（0）∈X，x∈X；

② 对每一个i，用高斯分布的方式生成一个局部随机序列{ξki}k≥0。

2） 迭代

① 计算平均权重θi（k+1）=∑nj=1[Φ（k）ij]xj（k-cji（k））=∑n（q+1）j=1[Φ（k）ij]xj；

② 计算xi（k+1）=ΠX[θi（k+1）-ηkgui（xi（k））]，这里ΠX[x]代表向量x到集合X上的投影，通过投影将约束集中的个体与其他个体分开，只讨论在约束集中的个体。

这里的ηk>0是迭代步长，且步长满足：

ηk>0，∑∞k=0ηk=∞，∑∞k=0η2k<∞。

随机无梯度的预测值可表示为：

gui（xi（k））=

hi（xi（k）+uiξi（k））-hi（xi（k））uiξi（k）

32系统扩维

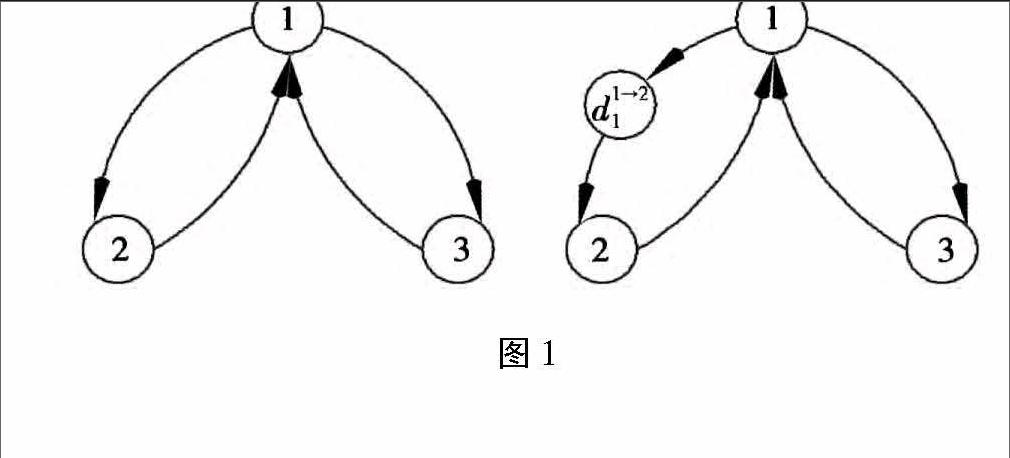
为了方便研究时延情形下的分布式随机无梯度优化算法的收敛性，下面将介绍如何利用系统扩维把有时延的优化问题转化为无时延的优化问题。在网络图G（k）中增加一些虚拟节点（见图1），这些节点的作用只是为了消耗信息在系统传递中的时延，自身没有自环。和增加的虚拟节点相比，网络中真实存在的点不仅可以传递信息，自己也可以处理信息。因此可以看出，虚拟节点只起到信息传递的作用，而不参与算法的迭代。

由于每个时刻通信网络每条边上的时延cij（k）都是不同的，所以令q=max ij。原来系统中的n个节点增加nq个节点即扩维后的多个体系统，共有n+nq个节点。为了不影响优化式（1），假设新增的时延个体所对应的局部目标函数值均为零。系统扩维后的权重矩阵为Φ（k）=[Φ1（k），Φ2（k）]T，其中[Φ1（k）]i，nl+j=（Φ（k））ij，l=cij（k）

0，otherwise，Φ2（k）=[Inq，0nq×n]，对于任意的l=1，2…q，i，j∈I，可以看出Φ（k）仍为行随机矩阵，但其主对角元素已不再是全部为正，因此无时延情形下的文献[7]，[8]，[13]的方法对本文都不再适用。

4收敛性分析

首先，做出如下假设：

假设1对于有向图G以及任意有向边上的时变时延cij（k），有：

1）有向图G是强连通图，其所对应的邻接矩阵Φ（k）是行随机的，而不一定是双随机的；

2）假设0≤cij（k）≤ij（k）<∞，即时变时延有界，令q=max（vi，vj）∈Eij

为了方便分析DRGF算法的收敛性，给出下列引理：

引理1[7]1 122对每一个i∈V有以下结论成立：

1） hiui （x）是可微凸集并且满足：

hi（x）≤hiui （x）≤muiG0（hi）

2） 梯度hiui （xi（k））满足：

E[giuixi（k）|Hk]=hiui （xi（k））

3）随机无梯度的预测值gui（xi（k））满足：

E[giui xi（k）|Hk]≤（m+4）2G20 （hi）

引理2[2]777令Ψ（k·s）=[Φ（k）Φ（k-1），…Φ（s）]，则可得以下结论：

1） 当k→+∞时，Ψ（k，s）的每一列[Ψ（k，s）]j收敛到一个正向量j（s）1，即：limk→+∞（[Ψ（k，s）]j-j（s）1）=0对所有j∈{1，2，…，n（q+1）}都成立。这里j（s）>0且∑n（q+1）j=1j（s）=1。

2） 存在一个正整数ν和一个非负数0≤α<1，使得：‖[Ψ（k，s）]ij-j（s）‖≤（q+1）4n4αk-s-3M-MvMv‖Ψ（s，s）‖j对所有i，j∈{1，…，q}和所有k≥s成立。

定理1在假设1，引理1成立的情况下，用上述DRGF法生成一个序列{xi（k）}k≥0，这里假设每一个hi都是Lipschitz连续的， 则对每一个t≥1和 j∈V，有：

定理1给出了目标函数的期望值E和最优值h（x*）之间的误差，不难看出，该误差和个体数n，系统扩维后增加的节点数nq，迭代步长η和Lipschitz常数有关。由定理1看出只要通信时延cij有上界，算法依然收敛。当cij=0时，则转化为无时延的情况。此外，还可以看出，时延情形下的迭代误差比无时延的迭代误差大，这表明若个体在信息交流的过程中存在通信时延，则会对个体间协同解决优化问题造成一定的影响。

推论1当假设1成立时，用上述方法生成一个序列{xi（k）}k≥0，步长为{ηk}k≥0且limk→∞ηk=。则有：

由推论1可以看出个体i在k时刻的状态xi（k）收敛到k时刻所有个体状态的平均值k。即此时多个体状态达到平均一致。此外多个体优化问题此时也取得最优值。

定理2在上述引理1，引理2以及推论1成立的前提下，又假设：若limk→∞ηk=且=0，则∑∞k=0ηk=∞。则有如下结论成立：

lim supt→∞E[f（j（t））]≤m 0∑n（q+1）i=1μi+D0 （16）

其中D=（n（q+1））（m+5）2（92+2（n（（q+1））/B2（1-）））

证明首先易得：

∑∞k=0ηk=∞，limt→∞1∑t-1k=0ηk12∑n（q+1）i=1E[‖xi（0）-x*‖2]=0 （17）

且有：lim supk→∞∑t-1k=0η2k∑t-1k=0ηk≤lim supk→∞ηk=

则

lim supt→∞1∑t-1k=0ηk12（n（q+1））（m+4）2 20 ∑t-1k=0η2k≤

12（n（q+1））（m+4）220 （18）

将推论1中的结论带入式（18）得

lim supt→∞1∑t-1k=0ηk（n（q+1））（m+

5）0∑t-1k=0ηkΩk≤2（n（q+1））（m+4）（m+

5）（2+n（q+1）α2（1-））20 （19）

利用定理1，将式（18）～式（19）带入式（10），最终可得：

lim supt→∞E[h（j（t））]-h*≤m 0∑n（q+1））i=1ui+

12（n（q+1））（m+4）220 +2（n（q+1））（m+

4）（m+5）×（2+n（q+1）α2（1-））20 （20）

事实上，定理2表明误差值lim supt→∞

E[h（j（t））]-h*是由两个方面来决定的。一方面是式（7）中所呈现的误差值，由于原始局部目标函数hi（x）的次梯度不存在或很难计算，用高斯近似函数hiμi （x）来代替hi（x），从而导致了该误差。另一方面，迭代步长在迭代的过程中逐步减小而ηk>0始终成立， 事实上， 当ηk=0时， 式（17）右侧变为lim supt→∞E[h（j（t））]-h*≤m0∑n（q+1）i=1μi，可见此时的误差值和约束集的维数m，lipschitz常数以及系统扩维所增加的时延节点数nq有关。

6结束语

在文献[2，7]的基础上，本文研究了时延情形下的分布式随机无梯度优化算法。首先给出时延情形下的分布式随机无梯度方法，然后通过系统扩维将时延优化问题转化为无时延优化问题，并利用转移矩阵的相关结论分析并证明了其收敛性。当然，还有一些问题有待解决，比如在无向图网络拓扑下中有时延的随机无梯度算法以及切换网络下的优化算法。

参考文献：

[1]NEDIA，OZDAGLAR A. Distributed Subgradient Methods for Multi-Agent Optimization[J].IEEE Transactions on Automatic Control，2009， 54（1）：48-61.

[2]NEDI A， OZDAGLAR A， PARRILO P A. Constrained Consensus and Optimization in Multi-Agent Networks [J]. IEEE Transactions on Automatic Control， 2010， 55（4）：922-938.

[3]SUNDHAR RAM S， NEDI A， V VEERAVALLI V. Distributed Stochastic Subgradient Projection Algorithms for Convex Optimization [J]. Journal of Optimization Theory & Applications， 2010， 147（3）：516-545.

[4]D Y，S X，H Z.Distributed Primal—Dual Subgradient Method for Multiagent Optimization via Consensus Algorithms[J].IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics， 2011，41（6）：1 715-1 724.

[5]DUCHI J， AGARWAL A， WAINWRIGHT M. Dual Averaging for Distributed Optimization： Convergence Analysis and Network Scaling [J]. IEEE Transactions on Automatic Control， 2012， 57（3）：592-606.

[6]TSIANOS K I， LAWLOR S， RABBAT M G. Push-Sum Distributed Dual Averaging for convex optimization [C]// IEEE Conference on Decision & Control， 2012.

[7]NESTEROV Y. Random gradient-free minimization of convex functions [J]. General Information， international association for research and teaching， 2011， 36（16）：1 112-1 142

[8]LI J， WU C， WU Z， et al. Gradient-free method for nonsmooth distributed optimization [J]. Journal of Global Optimization， 2015， 61：325-340.

[9]YUAN D， HO D W C. Randomized Gradient-Free Method for Multiagent Optimization Over Time-Varying Networks [J]. IEEE Transactions on Neural Networks & Learning Systems， 2015， 26：1 342-1 347.

[10]TSIANOS K I， RABBAT M G. Distributed consensus and optimization under communication delays[C]//49th Annual Allerton Conference on Communication， Control， and Computing， 2011：974-982.

[11]李德权，张晓倩. 时延情形下的分布式Push-sum 次梯度优化算法的研究[J].安徽理工大学学报（自然科学版），2015，35（2）：6-12.

[12]刘德进， 刘成林. 具有通信时延的离散时间二阶多个体网络的一致性问题[J]. 控制理论与应用， 2010， 27（8）：1 108-1 158.

[13]A BONDY J，S R MURTY U，A BONDY J，et al. Graph Theory with Applications[J]. American Elsevier Publishing Co.inc.new York，1976，62（419）：379-381.