Differential Game Based Link Resource Management for Next Generation Optical Network
Haitao Xu*, Yuqiong Cao, Shengsong Yang Xianwei Zhou
1 School of Computer and Communication Engineering, University of Science and Technology Beijing, Beijing 100083, China
2 China Academy of Information and Communications Technology, Beijing 100083, Beijing, China
* The corresponding author, email:alex_xuht@hotmail.com
I. INTRODUCTION
Nowadays, huge data are generating every seconds due to the significant development of the internet and various business types. With the advantages of high bandwidth and low loss, optical network is considered as a main support technology of the next generation network. Resource utilization in the next generation optical network is inefficient, causing a large number of internal fragmentations.And because of the coarseness characteristics,the traditional resource management schemes cannot satisfy the explosive demands in the next generation optical network, which may cause a waste of resources. Link resource management has become one of the most important issues in the foundation of the next generation optical networks [1-3], to efficiently and dynamically allocate resources to links based on services demands. As link resource management should satisfy the requirements on spectrum, it is essential to design a novel resource management algorithm to overcome the spectrum allocation problem and to break the limitations.
Lots of works have been down [4-7] to solve the allocation problems and to break the spectrum limitations in the next generation optimal network. In [4], a novel model considered transmission impairments and service classification is proposed to dynamically allocate link resources in optical network. It presents a heuristic min-cost algorithm and offers differential QoS(Quality of Services) in the optical domain with different grades. In [5],a SDN-based resource allocation algorithm is proposed with a real-time SDN controller platform. It presents a virtual architecture for optical network, and implements a SDN based control algorithm considered request priori-ties. In [6], a novel dynamic resource allocation algorithm is proposed based on the global concurrent optimization, and a VON resource broker is implemented to lower the blocking rate of optical requests and to enhance the utility efficiency of available optical network resources. In [7], a QoS guaranteed optical resource allocation strategy is introduced to increase bandwidth efficiency. The proposed model is evaluated on the probabilities of error and outrage to show out the effectiveness.
In order to achieve cost minimization in the process of resource allocation, the authors proposed a differential game based link resource management model in optical networks.
Game theory can be used to solve resource allocation problem of system with conflicting components. It has recently receiving an increasing interest in the context of [8-10].Compared with the existing algorithms, in this paper, a differential game based link resource management model is proposed to automatically control link resources and to increase resource utilization efficiency in optical network. Differential game theory is a powerful tool to solve the conflict problems in wireless networks. It can use the differential equations to describe the dynamic behaviours of the system. Lots works have been down to use the differential game to solve the bandwidth control problems [11], power control problems[12], and routing problems [13]. In our model,we use the differential game to solve the link resource management problems. Each links are considered as the rational and selfish game players. The whole resource management process is constructed as a cost function, considering the bandwidth resources, and the optical signal noise ratio (OSNR) degradation, to increase spectrum efficiency. The dynamic variations of the capacity is described by the differential equations, which are the constraints limits of the optimal system. The optimal link management can be obtained through the Nash equilibrium, which is achieved through the proposed algorithms. The key optimization method is based on a differential game model,which was firstly introduced by Dixit [14], being used for pollution analysis by Yeung [15].
The whole paper is organized as follows.We will describe resource allocation model and assumptions for the game model in Section II. In Section III, differential game based link resource allocation is given, and equilibrium solutions to the game is discussed. Section IV gives out the numerical simulation results.The work is concluded in Section V.
Link resource management of optical network with the aim of minimizing the cost for each optical link is researched in this section. Transmission bandwidth will be allocated based on the solutions of the proposed differential game. Letdenote the set of optical links.is the bandwidth demand of optical linkat time. The cost function defines the relationships between the “payments”and bandwidth, which is a linear form of the amount of bandwidthLetdenote the instantaneous “payment”, which is a linear function of the bandwidthand can be expressed as follows,
II. SYSTEM MODEL

The optical signal noise ratio (OSNR) at optical linkat timeis given by,

which can be expressed as follows,


Based on the above assumptions, the total cost function of the link to have a specific amount of bandwidth at timecan be expressed as follows, which is a linear combination,
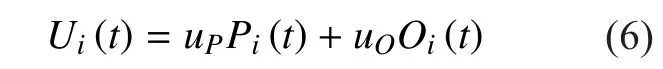

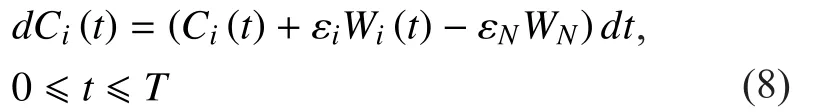
In the link resource management problem,each link takes an actionover the time period to minimize the total cost given in (7). The optimal allocated bandwidthcan be given by the following equation (9) shown in the bottom at this page.
III. DIFFERENTIAL GAME FORMULATION
In this section, we will discuss the differential game based on Hamilton-Jacobi-Bellman(HJB) equations. Feedback Nash equilibriums to the proposed game will be given. The dynamic optimization program technique was developed by Bellman [17-19]. According to Bellman’s dynamic programming principle,the allocated bandwidth should be optimal for the given time duration.
Definition 1(Bellman’s Dynamic Programming): A set of actionsconstitutes an optimal solution to the control problem (9) if there exist continuously differentiable functionsdefined onand satisfying the following Hamilton-Jacobi-Bellman (HJB) equations,

where


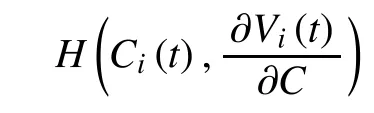



In order to obtain the Nash equilibrium solutions for the optimization problem, firstly,we need to prove the existence of the Nash equilibrium. Generally, the existence can be proved through the derivatives. Performing the indicated minimization for the optimization problem indicated above, we can get,

Based on the above equations, it is obviously that the Nash equilibrium to the proposed differential game exists. The Nash equilibrium for the optimization problems can be viewed as a set of equations

Algorithm Load balancing Mechanism

Proposition 1: The value functionadmits a solution, which can be expressed as follows:


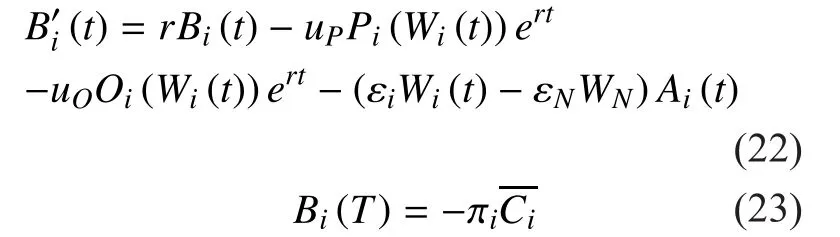
Proof:See the Appendix.
Since the solutions to the value functionis obtained through (19-23), we can get the expression of the optimal bandwidth allocated to linkas follows,

The algorithm based on the Nash Equilibrium is shown in the following section. The complexity of the proposed algorithm isThe flow chart based on the algorithm is given in figure 1.
IV. NUMERICAL SIMULATIONS
In this section, we will discuss the numerical simulations for the differential game and the resource allocation management algorithm in section III. We consider a scenario using the proposed differential game to control the allocated resource for each optical link. The numerical simulations is based on Matlab environment and the main simulation parameters are given in table 1 and table 2.

Figure 4 and figure 5 give out the optimal allocated resource to each link. The vary trends ofwith time and discount rate respectively. We can observe that the convergence speed of the allocated resource for each link is quick enough to obtain the optimal solutions in the limited time period. It is noted that the variation ofis inverse proportion to the variation ofAs shown by figure 3 and figure 4, the proposed game model can achieve Nash equilibrium in the link resource management, and the optimal allocated resource for each optical link is just the Nash equilibrium solution of differential games.
V. CONCLUSION
In this paper, we have proposed a differential game based link resource management model in optical networks, to achieve cost minimization in the process of resource allocation. The performance of link resource management approach has been analyzed based on the dynamic programming principle. The Nash equilibriums are solved to get the optimal allocated resources. A novel algorithm for the link resource management is proposed based on the equilibrium solutions. Numerical results are given to show the model performance.

Fig. 1 Algorithm flow chart

Fig. 2 Vary trends ofwith time
ACKNOWLEDGEMENTS

Fig. 3 Vary trends ofwith discount rate

Fig. 4 Vary trends of optimal allocated bandwidth with time

Table I Main simulation parameters
We gratefully acknowledge anonymous reviewers who read drafts and made many helpful suggestions. This paper is supported by National Science Foundation Project of P. R. China (No. 61501026, U1603116), the Fundamental Research Funds for the Central Universities (No. FRF-TP-15-032A1).
Appendix
In this part, we will give the proof of Proposition 1
Based on the dynamic programming, assumingis a polynomial that can be expressed as follows:

Based on equation (24), we can get the derivative of theas follows:

Taking equation (25) and (26) into the Bellman’s Dynamic Programming system, we can get:

Then we have the dynamic programming system expressed as follows

In order to have all the equations equal to zero for all links during the periodwe have

Then we have
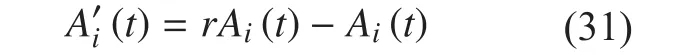
And


Then we have

Plugging the terminal cost equation ofinto equation (31), we have

Fig. 5 Vary trends of optimal allocated bandwidth with discount rate

Table II Values parameters

[1] K. Sivalingam, S. Subramaniam, “Optical WDM Networks: Principles and Practice,” Boston: Kluwer, 2000.
[2] G. H. Sasaki, C. F. Su, “The interface between IP and WDM and its eff ect on the cost of survivability,” IEEE Communication. Magazine, vol. 41,no. 1, 2003, pp.74-79.
[3] A. McGuire, S. Mirza, D. Freeland, “Application of control plane technology to dynamic configuration management,” IEEE Communication.Magazine, vol. 39, no. 9, 2001, pp.94-99.
[4] Y. Tang, M. Rao, L. Li, et al, “A novel model on dynamic resource allocation in optical networks,” Science in China Series F: Information Sciences, vol. 48, no. 1, 2005, pp.15-27.
[5] J. Wang, N. Cvijetic, K. Kanonakis, et al, “Novel Optical Access Network Virtualization and Dynamic Resource Allocation Algorithms for the Internet of Things,” Optical Fiber Communication Conference, Optical Society of America,2015: Tu2E. 3.
[6] R. Vilalta, R. Muñoz, R. Casellas, et al, “Virtual optical network resource allocation using PCE global concurrent optimization for dynamic deployment of virtual GMPLS-controlled WSON,”Journal of Optical Communications and Networking, vol.5, no.12, 2013, pp.1373-1381.
[7] H. Beyranvand, J. A. Salehi, “Efficient optical resource allocation and QoS differentiation in optical burst switching networks utilizing hybrid WDM/OCDM,” Lightwave Technology, Journal of,vol.30, no.15, 2012, pp.2427-2441.
[8] J. Zhao, W. Zheng, X. Wen, et al, “Game theory based energy-aware uplink resource allocation in OFDMA femtocell networks,” International Journal of Distributed Sensor Networks, vol.10,no.3, 2014, pp.658158.
[9] J. Zhao, H. Zhang, Z. Lu, et al, “Coordinated interference management based on potential game in multicell OFDMA networks with diverse QoS guarantee,” Vehicular Technology Conference (VTC Spring), 2014 IEEE 79th. IEEE,2014, pp.1-5.
[10] W. Zheng, T. Su, H. Zhang, et al, “Distributed power optimization for spectrum-sharing femtocell networks: A fictitious game approach,”Journal of Network and Computer Applications,vol, no.37, 2014, pp.315-322.
[11] L. Zhang, X. Zhou, J. Guo, “Noncooperative dynamic routing with bandwidth constraint in intermittently connected deep space information networks under scheduled contacts”, Wireless Personal Communications, vol. 68, no. 4, 2013,pp. 1255–1285.
[12] L. Zhang, X. Zhou, “Joint cross-layer optimised routing and dynamic power allocation in deep space information networks under predictable contacts”, IET Communications, vol. 7, no. 5,2013, pp. 417–429.
[13] L. Zhang, W. Huang, X. Miao, and W. Cao, “The impact of storage capacity usage and predictable contact schedule on dynamic routing for opportunistic deep space information net-works”, Wireless Personal Communications, vol.77, no. 2, 2014, pp. 1377–1395.
[14] Dixit A, “A model of duopoly suggesting a theory of entry barriers,” General Information, 1979,pp.20-32.
[15] Yeung D W K, “Dynamically consistent cooperative solution in a diff erential game of transboundary industrial pollution,” Journal of optimization theory and applications, vol. 134, no.1,2007, pp.143-160.
[16] H. Xu, X. Zhou, “Optimal Power Control in Cooperative Relay Networks Based on a Differential Game,” Etri Journal, vol.36, no.2, 2014,pp.280-285.
[17] D.W.K. Yeung, and L.A. Petrosyan, “Cooperative stochastic diff erential games,” Springer Series in Operations Research and Financial Engineering,Springer Press, 2006.
[18] Z. Zhu, S. Lambotharan, W. H. Chin, et al, “A Game Theoretic Optimization Framework for Home Demand Management Incorporating Local Energy Resources,” IEEE Transactions on Industrial Informatics, vol.11, no.2, 2015, pp:1-1.
[19] Osborne, J. Martin, “An introduction to game theory,” Oxford University Press, vol.9, no.3,2004, pp.841-846.
- China Communications的其它文章
- A Privacy-Based SLA Violation Detection Model for the Security of Cloud Computing
- Empathizing with Emotional Robot Based on Cognition Reappraisal
- Light Weight Cryptographic Address Generation (LWCGA) Using System State Entropy Gathering for IPv6 Based MANETs
- A Flow-Based Authentication Handover Mechanism for Multi-Domain SDN Mobility Environment
- An Aware-Scheduling Security Architecture with Priority-Equal Multi-Controller for SDN
- Homomorphic Error-Control Codes for Linear Network Coding in Packet Networks

