以反治本策略的实践与思考
☉江苏省泰兴中学 游 洋
以反治本策略的实践与思考
☉江苏省泰兴中学 游 洋
中学数学教师都有这样的教学共识:很多问题教师反复讲、学生反复练,但是以前犯过的错误今天还是继续犯错,在典型的错误问题前面,这种反复显得非常苍白无力.这是为什么呢?作为拥有多年教学经验的教师,我们思考过为什么吗?如何办呢?笔者以为,教师都思考过,但是这些典型的错误学生却总是再犯,说明我们的教学方法亟需改进.
心理学研究表明,要让知识记忆深刻最好的方式是允许犯错,并从错误中获得理解.对于一些普遍犯错的问题,教师教了多年并未改善,是否可以从学生的自身反思中获得提高?因此以反治本的策略恰恰是为了解决那些根深蒂固的错误,也是减少教学中在这些无法提高正确率问题的新的教学策略.
一、以剖析反思的方式以反治本
错误问题继续错误,这是学生数学学习的一个典型现状.教师面对这样的教学现状,采用最多的教学方式是反复讲、反复训练,但是效果呢?教师依旧常常抱怨:一届一届学生,错误总是这么几个,愈来愈不会教了.笔者想问:这难道是学生之过?还是要从教学方式上做出重要的改变.从单遵教授的观点来看,错误之所以重复有两个原因,第一是学生不理解这一知识的内涵,第二是错误是教师告诉他的,他自身未能及时发现和反馈.因此,笔者认为要处理学生典型错误的最有效、最好的方式是以错题为例进行剖析、自我反思、以反治本.
问题1:已知集合A={x|x2+x-6=0},B={ax+1=0},满足B⊆A,求实数a能取的一切可能值所组成的集合.

类似训练:当a为何值时,不等式(a2-1)x2-(a-1)x-1<0的解集为全体实数?
生:我把原不等式简单地看成一个一元二次不等式,总是把问题想当然.事实上,当二次项系数a2-1=0时,即a=±1时,它不是一元二次不等式,经过检验可知,当a=1
温馨提示:从自我剖析、反思的方式以反治本,有效地触及了学生的内心,从学生认真分析的状态中,我们发现了其反思自身问题解决的不全面性,向其他学生用心阐述了错误的因素.这种类似陶行知先生的“小先生制”大大地激发了学生解决典型错误的有效性,笔者发现历经以反治本的策略,部分学生在问题上的错误大大降低,获得了一定的进步.
二、以同题异构的方式以反治本
很多问题是类似的,但是解决的方法并不是一致的,或者有些问题教师描述的方式方法,学生总是不喜欢用,而是一味地选择自己的方式方法,这样做的后果是学生有时做对了,有时做错了,因为其并未找到问题犯错的本质,导致其后续用的还是老方式、老步骤.笔者认为以同题异构的方式,让多位学生共同展示不同的解决方法,从异构中区分方法的优劣性是以反治本的好途径.
问题2:图1为函数y=Asin(ωx+φ)的图像的一段.
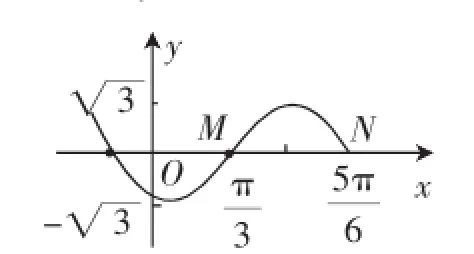
图1
(1)求其解析式;
请学生板演问题解决思路(主要研究第(1)问).
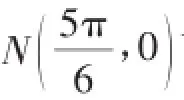
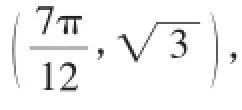
辨析:请学生思考哪些解法是优秀的?哪些是不合时宜的?以后在已知图像后如何解决y=Asin(ωx+φ)的解析式更为恰当?(学生合作讨论,以讨论的方式获得更多的经验)
生(总结):我们讨论后一致认为思路1和思路2是正确的,也是非常好的方法.思路3貌似很简单,但是产生了增根,在具体解决问题时还需进一步检验,反而显得累赘了.
师:请你说一说理由是什么?
生:先说思路3错误的原因,因为用到的是函数的平衡点,所以看上去计算量简化了很多,但是却解出了两个不同的φ值.我们验证了一下,发现其中一个恰为图2中的虚线图形,另一个为正解.出现这样的原因正是因为使用了平衡点!平衡点处有两个函数均从这里穿过,这就导致无法确认哪一个才是题意需要的,所以必须检验.思路1比较合理地使用了我们课堂上讲的“五点法”,这首先要求大家必须牢记正弦函数y=sinx的基本形态,要正确看待点M在五点中所处的具体位置,只有弄清了位置才能计算φ值;思路2显得更随意一些,只要找到最值点即可解决唯一的φ值,究其原因是最值点不可能两个函数共同经过,所以很好地解决了问题.
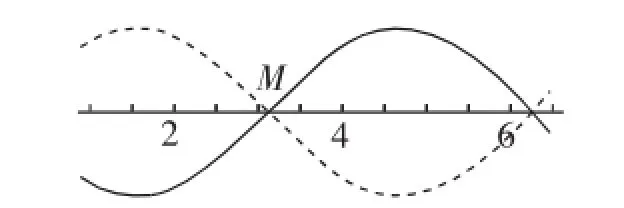
图2
温馨提示:通过同题异构,我们认识到了同学们常常犯的一个错误——用平衡点去计算φ值,这种貌似简单明了的方式却往往容易产生错误,而“五点法”很好地给予了点位置上的确定性,不易错误,最值法较好的固定了函数图像的走势,不易错误,希望大家有所启发.
三、以重视思想的方式以反治本
数学中高端层次的问题往往具备了一定的数学思想指导,在数学思想指导下有些问题的解决显得较为容易,如何去发现问题背后隐藏的数学思想?如何引导这种思想以反治本?这是教师在教学时需要关注的.
问题3:(教材习题)等差数列{an}的前n项和Sn=m,前m项和Sm=n(m≠n),求前m+n项的和Sm+n.

温馨提示:本问题的处理看似简单,实际上是数学思想在背后的运用.数列问题都是离散型函数模型的体现,即函数与方程思想是解决的问题的主要导向.笔者首先让学生动手验算本例,在经过数十分钟运算后,学生纷纷表示,字母多、求解方向不清晰,导致学生很盲目.有了前面的困扰,那么以反治本的手段——数学思想找到时机恰到好处的引入,让学生迅速了解了函数与方程思想在数列章节中的重要性,也一语中的阐述了数列本质,获得了问题解决的更多思考.
总之,以反治本是教学的一种手段,其需要给予学生足够的时间探索、允许其犯错,要从学生自身的学习中去获得经验积累,这种手段在学生不断重复的错误问题上有良好的效益,值得教学尝试探索.
1.徐晓红.纠正思维顽疾之利器——以反治本[J].数学教学研究,2010(2).
2.吴成海.数学试题创新应着力于思维培养[J].中学数学,2013(8).
3.王建鹏.一道试题的析题展示[J].福建中学数学,2013(9).F

