例谈利用必要条件缩小参数范围在解题中的运用
——从一道模拟题说起

☉江苏省盐城市伍佑中学 高小勇

例谈利用必要条件缩小参数范围在解题中的运用
——从一道模拟题说起

☉江苏省盐城市伍佑中学 高小勇

含参不等式的求解是近年来全国各地高考数学、竞赛数学的考查热点.这类问题既含参数又含变量，往往与函数、数列、方程、几何等有机结合起来，常与不同知识交汇，其综合性强，解法灵活，思维要求高，往往令很多同学望而生畏.学生解决此类问题往往力不从心，讨论问题不全面.本文从一道模拟题开始谈谈如何利用必要条件来缩小范围入手，优化解题过程.

一、题目再现

二、学生的解答思路展示

解法2：变量分离，将要求的式子转化为a（1+xlnx）≥-xlnx，再转化为

由此可知，学生在处理这类恒成立问题时的方法是没有问题的，但是由于其中涉及分类讨论，有时涉及的函数复杂，学生很难将问题进行到底.笔者结合学生遇到的实际问题，利用必要条件将范围缩小后，优化了解题过程.

三、利用必要条件缩小范围后的解法

解法1（直接构造含参函数）：f（x）≤x恒成立可转化为a+（a+1）xlnx≥0恒成立.

令φ（x）=a+（a+1）xlnx，x∈（0，+∞），则φ（x）≥0对任意x∈（0，+∞）恒成立，那么φ（1）≥0，从而得到a≥0.

易知a=0不成立，所以a＞0，a+1＞1.

又因为φ′（x）=（a+1）（1+lnx），

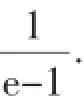
解法2（分离参数）：f（x）≤x恒成立可转化为a+（a+1）· xlnx≥0恒成立，则（a+1）xlnx≥-a.

因为a+（a+1）xlnx≥0对任意x∈（0，+∞）恒成立，所以x=1满足上述不等式，即a≥0.所以（a+1）xlnx≥-a可转化为

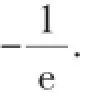
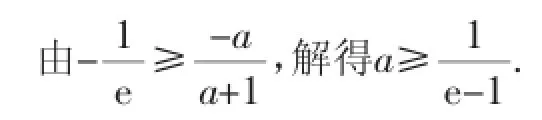
由上面两种方法的对比可以看出，先利用题目所给范围内的特殊值去缩小范围，在求函数最值时就可以减少分类讨论的情况，优化了解题过程.

这样的例题很多，下面列举几例加以说明：

例1若不等式x2-2mx+2m+1＞0对满足0≤x≤1的所有实数x都成立，求实数m的取值范围.

解：设（fx）=x2-2mx+2m+1，则本题等价于函数（fx）在0≤x≤1上的最小值大于0，求实数m的取值范围.

因为函数（fx）在0≤x≤1上的最小值大于0的必要条件是（f0）＞0，即2m+1＞0，也即

注：本题的解法一般是考虑m＜0，0≤m≤1，m＞1三种情况进行讨论.

解：不等式成立的必要条件是0≤b≤1，a＞0.下面讨论此条件成立.不等式x2+1≥ax+b转化为x2-ax+（1-b）≥0对任意x∈［0，+∞）成立的充要条件是

令f′（x）=0，得x=a-3.

当0＜x＜a-3时，f′（x）＜0；当x＞a-3时，f′（x）＞0，所以，当x=a-3时，（fx）取最小值.因此，（fx）≥0成立的充要条件是（fa-3）≥0，即a≥（2b）-12.

注：由于利用不等式成立的必要条件把a，b的取值范围缩小，使问题在一个较小的范围内进行解决，使得解题的难度大大降低.

例3设函数（fx）=x（ex-1）-ax2.若当x≥0时，（fx）≥0，求实数a的取值范围.

解：函数（fx）可化为f（x）=x（ex-1-ax）.根据不等式ex≥x+1，显然当a=1时，（fx）≥0成立，故a=1是不等式成立的必要条件.令g（x）=ex-1-ax，则g（′x）=ex-a.若a≤1，则当x∈（0，+∞）时，g′（x）＞0，g（x）为增函数，而g（0）=0，从而当x≥0时，g（x）≥0，即（fx）≥0.

若a＞1，则当x∈（0，lna）时，g′（x）＜0，g（x）为减函数，而g（0）=0，从而当x∈（0，lna）时，g（x）＜0，即（fx）＜0.

综合得实数a的取值范围为（-∞，1］.

注：发现a=1是不等式成立的必要条件，找到分类讨论的标准，为破解难题创造条件.

例4已知函数（fx）=ax2-lnx（a为常数）.

（2）若a＜0，且对任意的x∈［1，e］，（fx）＞（a-2）x恒成立，求实数a的取值范围.

解：（1）略.

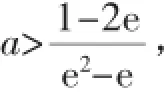
由此看出，恒成立问题作为高中阶段非常重要的一个问题，在掌握了解决恒成立问题的基本方法后，再结合特殊值缩小参数的范围可以大大简化问题的难度，增加学生的解题经验.