Two-Body Local-Momentum Approximation of Spinless Particles Scattered by a(1+1)-D Woods–Saxon Barrier Potential
Karl-Erik Thylwe
KTH-Mechanics,Royal Institute of Technology,S-10044 Stockholm,Sweden
1 Introduction
Recent research on relativistic two-body effects[1−5]apply a semi-relativistic(SRQ)quantum approximation.With a related approximate approach by Ikdair&Sever,[1]two-body phenomena of bound and scattering states can be estimated with methods of non-relativistic quantum mechanics.Two-body effects appear as bound-state level shifts as well as scattering resonance shifts.Such twobody shifts are primarily due to special relativity.Shifts due to particle spins are ignored in the present semirelativistic approach.
The approximation of the Bethe–Salpeter equation due to Ikdair&Sever[1]is a continuation of earlier ideas by Nickisch et al.,[6]leading to a Schrödinger-like equation.It has been questioned by Lucha et al.[2]for non-rigorous applications to bound-state calculations.Later research explains that the basic semi-relativistic quantum equation has exact solutions for step-like barriers to compare with,and that the approximation by Ikdair&Sever accurately predicts transmission and reflection coefficients for(1+1)-D dynamics.[5]
The idea by Ikdair&Sever is different from other approaches,like those in Refs.[7–9].Ikdair&Sever directly quantize the energy-momentum invariant of special relativity.Required methods with this approach are familiar in non-relativistic quantum mechanics,as is obvious in recent applications assuming that relativistic contributions are small.[3−4]Most of these applications focus on bound states in(1+1)dimensions(D)and in(1+3)-D.A couple of applications are related to scattering problems,see Refs.[4–5]for(1+1)-D barrier-type interaction potentials.However,early applications to bound and scattering states do not discuss two-body effects,but rather analytic solution methods for specific potential shapes.The present local momentum(LM)approximation of the SRQ approach,also leading to a Schrödinger-like equation,is related to the exact SRQ treatment in Ref.[5],where a rectangular barrier was studied by matching linear plane-wave solutions.
One can think of the LM-approximation as an“adiabatic”approximation of a quantum-mechanical theory starting from a classical Hamiltonian from the special relativity.Such a semi-relativistic quantum theory presently ignores particle spin.The basic SRQ equation is still diffi-cult to approach by standard numerical methods based on second-order ordinary differential equations(ODE).The main mathematical obstacle is the presence of squareroot operators in the basic SRQ formulations.In subsequent sections the basic SRQ equation is simpli fied by further(adiabatic)approximations resulting in a secondorder ODE.Once the Schrödinger-like equations are obtained,one can apply any standard numerical method of quantum mechanics.Here,the Milne’s numerical method is used,as explained elsewhere.[11−13]
Two potential models are considered:The rectangular barrier,which allows exact numerical SRQ comparisons,is given by

Note that Alhaidari et al.[14]studied transmission properties for a single fermion mass with scalar/vector-type rectangular barriers using Dirac theory.
The second model is an inverted Woods–Saxon poten-tial,a Woods–Saxon barrier,is given by

whereV0represents the potential strength,dis a length representing the “surface thickness” of nuclei,andarepresents the effective size of nuclei.The parametersaanddare varied in the present study.Note that Thomson[16]also studied transmission properties for a single fermion mass with scalar/vector-type Woods–Saxon barriers using Dirac theory.
From an earlier study of the rectangular(1+1)Dbarrier model,[5]it became clear that the approximation by Ikhdair&Sever,[1]here called the generalized Schrödinger(GS)approximation,is accurate with weak relativistic conditions on potential parameters.A critical parameter is the barrier strengthV0,which causes extraordinary transmission behaviors forV0larger thanm2c2,wherem2is the smaller of the two masses.For such values it is not obvious that the GS-and the LM approximations would agree for rectangular barriers,and even less obvious for smooth barriers like the Woods–Saxon barrier.
Section 2 describes the basic equations of the semirelativistic quantum approach.The amplitude-phase approach is presented in Sec.3.The particular LM approach is discussed in Sec.4.Various approximations of the LM approach is presented in the same section,in particular the approximation of Ikhdair&Sever and the non-relativistic(Schrödinger)limit.Numerical and graphical results are shown in Sec.5,and a conclusion is in Sec.6.
2 Semi-Relativistic(SRQ)Two-Body Quantum Equation
The SRQ differential equation in the center-of-mass frame for relative motion of the massesm1andm2is linear,and given by[5]

whereϵis the dynamical energy(total energy minus restmass energies).The operator L,including a relativistic(time-like)vector-type potentialV,is given by

The operator L is linear,and far away from the interaction the solutions are plane waves(ψ±k=e±ikx)with an asymptotic wave numberk.The plane waves satisfy Eq.(3),

wherem=m1+m2is the total mass.An explicit relation between the wave numberkand the energyϵis
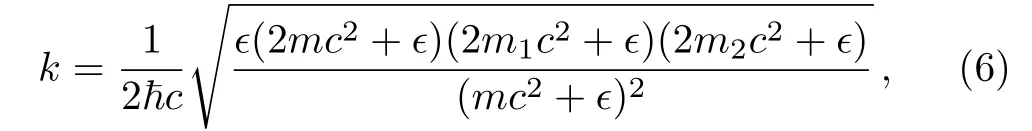
which reduces to the non-relativistic(NR)expression

asc→+∞.The symbolµis the reduced mass

In the presence of a potential that vanishes as|x|→∞the boundary conditions for the scattering wave function Ψ can be written as

wheretandrare the transmission and reflection amplitudes,respectively.Expressions for the transmission and reflection coefficients are:

These quantities are computed with the aid of Secs.3 and 4 for the rectangular and the Woods–Saxon potentials by the amplitude-phase method.Results are presented in Sec.5 and further discussed in Sec.6.
3 Schrödinger-Like Equations and the Amplitude-Phase Method
In this study the relevant approximations of the SRQ equation(3)are defined by Schrödinger-like equations;see the subsequent sections.Hence,the approximate solutions are obtained from

with a variable coefficient functionK2(x),and one can apply standard numerical method of quantum mechanics to solve the barrier problem.In the present study the amplitude-phase method is applied.[11−12]It is based on two amplitude-phase representations,left(L)-and right(R)representations,of fundamental solutions satisfying Eq.(13).These are

where Eq.(15)is an auxiliary relation ensuring the Wronskian determinant of the two(±)-solutions(14)being constant.This condition can be imposed since the number of symbols is doubled.Inserting Eq.(14)into the Schrödinger-like equation(13),one obtains a nonlinear Milne equation[12]

From the twoL,R-representations(14)and(15)one defines fundamental matrix solutions

where a prime,′,indicates a derivative with respect tox.The fundamental solutions are matched at the originx=0 as described in Ref.[11].The resultingL,R-connection is

In the present case the barrier is symmetric with respect tox=0,and one can use amplitude solutions of Eq.(16)satisfying

Hence,the matrix(19)can be written directly in terms of amplitude values,i.e.

The transmission-and reflection coefficients are obtained as

and by direct evaluations of the M-matrix elements the resulting expressions become

The reflection symmetry of the present potential implies that Eq.(26)can be used.Hence,only one of the amplitude functions,sayAR(x),is to be integrated.For scattering solutions the Milne equation(16)is integrated from initial conditions at anyxinit≫a,whereais the range parameter,with

The constantK(+∞)>0 is the relevant asymptotic wave number.The integration terminates atx=0 and the valuesAR(0),(0)are inserted into Eq.(26).Results depend very little on position ofxinit≫aif the tail of the potential vanishes exponentially.For the Woods–Saxon potentialxinit≈10ais used.The numerical tolerance of the integrator is≈ 10−7.
The initial(boundary)conditions(27)are taken from an exact constant solution of the nonlinear equation(16)asx→+∞.The exact wave number in Eq.(6)is the relevant one for the local-momentum(LM)approximation presented in the subsequent section.
4 Local-Momentum(LM)Approximation
The aim of the LM-approximation is to obtain a Schrödinger-type differential equation instead of Eq.(3),and,thereby revealing a relation to the generalized Schrödinger(GS)approximation of Ikhdair&Severe.[1]
The key observation motivating a“local-momentum”approximation is this:the plane-wave solutionsψ±k=e±ikxsatisfy the original SRQ equation(3)as well as the second-order ODE:

wherekis defined in Eq.(6).Hence,for a vanishing potentialV,Eq.(3)can be replaced by Eq.(28),which appears as a “generating second-order differential equation”for Eq.(3).
An algebraic manipulation with the same resulting Eq.(28)is possible by assumingVbeing constant in Eq.(3)and treating the operatorˆp2as ac-number or a local function.The operator status ofˆp2is subsequently retained after the completed algebra,and the solution is exact.
The main approximation of such algebraic manipulations is that the potential has no derivatives in connected intervals of thex-axis.The solutions are linear and can be rigorously fitted at each discontinuity of thex-axis.
To generalize this situation one can instead of a discontinuity think of a smooth transition between two(almost)constant values ofV.The rectangular-shaped Woods–Saxon barrier is the potential model chosen for this purpose.Here it is proposed that a discontinuity can be replaced by a small(surface thickness)region with possibly large derivatives of the potential.
By heuristically assuming the potentialVbeing piecewise constant with sufficiently small transition regions,one obtains an equation(13)withK2(x)replaced by

or equivalently
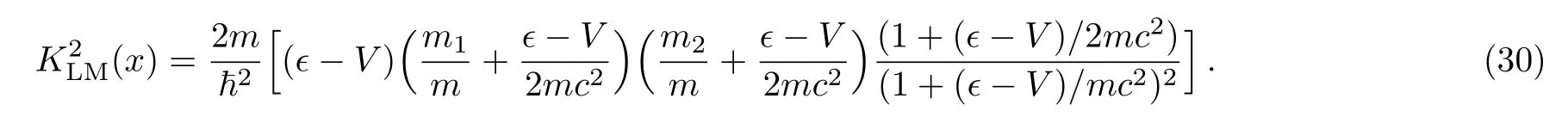
Contributions from derivatives of the potentialVare ignored in this study.
It is interesting to approximate the coefficient(x)in different limiting directions.Five particular cases are:
•The equal-mass situation:

•The extreme light-heavy situation:

•The weak,relativistic situation:

•The non-relativistic situation:

•The weak potential situation:

with expansion parameters

Note that the second case(32)does not imply“a single particle scattering in a potentialV”.Instead,one actually has a two-body scattering case here,where one of the particles is massless like a photon.Note also that the third case(33)is similar to the Schrödinger-type coefficient function of Ikhdair&Sever-approximation.[1]In this approximation the two-body mass index satisfies
近期,南海航海保障中心发布了《南海海域水上安全通信业务布局规划(2019年-2025年)》。《规划》按照深化航海保障体制改革要求,结合南海海域水上安全通信工作实际,提出了加大海区水上通信资源整合力度,加快海区水上通信现代化建设,争取在2025年前水上安全通信国际履约能力达到发达国家水平,全面满足海上用户对安全通信服务的需求的目标。其中,建立海区水上通信融合发展模式,实现“遇险安全通信统一值守、海上安全信息统一播发、主要通信设备统一管控、通信信息资源实时共享”是未来几年南海海区水上通信业务的总体发展思路。

Two of the above coefficient approximations,Eqs.(33)and(34),are applied numerically and included for comparisons with Eq.(30)in Tables 1–4.
5 Results for the(1+1)DRectangular and Woods–Saxon Barriers
The rectangular barrier case has analytic solutions of the transmission and reflection coefficients and allows exact semi-relativistic results.[5]The LM approximation becomes exact and the GS approximation turns out to be surprisingly accurate,although the GS-wave numbers are not particularly accurate in general.[5]The LM-and GS approximations suite the amplitude-phase method well.[11]
Both approximations result in differential equations of the Schrödinger type.Numerical values of the transmission coefficient reveals possible oscillatory behaviors at very low scattering energies and strongly repulsive barriers(see below).These are spectacular two-body effects that at the moment should be seen as hypothetical,but inherent to the “semi-relativistic” approach.For such parameter values(strong,repulsive barriers)the fundaments of the semi-relativistic approach are questionable.

Table 1 (Color online)Two-body transmission coefficients T for the rectangular barrier with parameters V0=2µ,a=3,m1=100µ,d=0,and varying scattering energies ϵ.Symbols in the table of the calculated transmission coefficient:T(exact analytic),TLM(numerical LM-calculations),TGS(Ikhdair&Sever),and TNR(non-relativistic).
For rectangular barriers the predictive power of two body effects of the GS approximation can be rigorously estimated;see Table 1. When the rectangular barrier becomes a smooth function ofx,both LM-and GS-approaches are approximate.For the Woods–Saxon barrier one can still study how the LM-and GS-approximations relate to each other as the surface thicknessdof the Woods–Saxon barrier increases.One can also study the relation to Dirac theory for a single fermion in a potential field.
5.1 Rectangular Barrier
In Ref.[5]it was shown that transmission properties for the light-heavy mass systems differ the most compared to non-relativistic calculations.Therefore the mass parameters in Table 1(rectangular potential)are chosen asm1=100µandµ=1.The potential strength isV0=2µc2in Table 1(rectangular potential),which is close to a critical value for which the waves become oscillatory in an extreme sub-barrier energy region(see Figs.2 and 3).Furthermore,the barrier range is chosen asa=3 in Table 1.

Fig.1 (Color online)Transmission coefficients for sharp (upper subplot)and smooth (lower subplot)Woods–Saxon barrier as function of ϵ/V0.Specific potential parameters are:V0=2µ,µ =1,m1=100µ,a=3,with d=0.01(upper subplot)and d=0.2(lower subplot).The LM-and GS-approximations are represented by the same continuous curves and the non-relativistic(NR)approximation by dashed-dotted curves.

Fig.2 (Color online)Dirac(upper subplot)and LM(lower subplot)computations of T for a Woods–Saxon barrier as function of ϵ/V0,where d=0.01,V0=3µc2,µ=1,a=1.Upper plot corresponds to results from Dirac computations with the single-particle massµ.The lower subplot corresponds to three cases of two-body SRQ computations.Black continuous curve represents m1=3.7µ,while blue dashed-dotted curve corresponds to m1=100µand blue dashed curve corresponds to m1=3µ.
Table 1 shows that the numerical local momentum approach agrees with the analytic exact results for the transmission coefficient,as expected.In Ref.[5]the generalized Schrödinger(GS)equation by Ikhdair&Sever[1]turned out to be accurate for moderate potential strengths.This accuracy is valid also in the present cases,in particular for the sub-barrier energy regions(not shown).However,the relative accuracy is gradually lost to between≈0.2%and≈2%in the super-barrier energy region(Table 1),where the transmission coefficient is oscillatory;see also Fig.1 for the Woods–Saxon potential.The non-relativistic approximation(TNR)is reasonably accurate only in the subbarrier energy region,and behaves similar to the dasheddotted lines in Fig.1.
5.2 Woods–Saxon Barrier
Hence,the numerical results show that the GS approximation is accurate even at the strong potential barrier withV0=2µc2,whereµ=1.This is twice the barrier height considered in Ref.[5].The only remarkable deviation between LM and GS results is at very low scattering energies.This difference is indicated also in the upper subplot(smalld)of Fig.1 for the Woods–Saxon barrier.It corresponds to the strange two-body effect of the SRQ equation mentioned earlier,but apparently exists for smooth(but sharp)barriers.An increase of the potential strength toV0>2µc2results in effects similar to single-mass phenomena discussed recently within the Dirac framework[14](see Fig.2).
Tables 2–4 show the transmission coefficient for the same potential strengthV0and sizeaas in Table 1,but with variable surface thicknessd=0.01,0.2,and 1.

Table 2 Two-body transmission coefficients T for the Wood–Saxon barrier with parameters V0=2µ,a=3,d=0.01,m1=100µ,and varying scattering energies ϵ.Symbols in the table of the calculated transmission coefficient:TLM(numerical LM-calculations),TGS(Ikhdair&Sever),and TNR(non-relativistic).
Table 2 studies the transmission coefficient of a Woods–Saxon barrier with a sharp surface(d=0.01).The results are approximately the same as in Table 1 for the rectangular barrier.In the upper subplot of Fig.1(d=0.01),corresponding to Table 2,the continuous curve represents LM-and GS computations.In contrast,the non-relativistic(dashed-dotted)curve in Fig.1(upper subplot)deviates more and more from the others with increasing scattering energy.

Table 3 Two-body transmission coefficients T for the inverted Wood–Saxon barrier with parameters V0=2µ,a=3,d=0.2,m1=100µ,and varying scattering energies ϵ.Symbols in the table of the calculated transmission coefficient:TLM,TGS(Ikhdair&Sever),and TNR(non-relativistic).
Table 3 and the lower subplot of Fig.1 show the transmission coefficient of a Woods–Saxon barrier with a less sharp surface(d=0.2).The agreement between GS-and LM results is even better.The oscillation amplitudes of the transmission coefficient have become smaller.Table 4 shows results from a non-rectangular barrier with surface thicknessd=1.The table shows a complete agreement between GS-and LM results.Non-relativistic results are also approximately the same.The approximations used here tend to be more similar as the surface thickness increases.

Table 4 Two-body transmission coefficients T for the inverted Wood–Saxon barrier with parameters V0=2µ,a=3,d=1,m1=100µ,and varying scattering energies ϵ.Symbols in the table of the calculated transmission coefficient:TLM(numerical LM-calculations),TGS(Ikhdair&Sever),and TNR(non-relativistic).
As a final study,the Woods–Saxon potential is used to compare SRQ results with the results of the(singlemass)Dirac theory as the surface thickness isd=0.01(see Refs.[14–15]).For such potentials there are speculative investigations about zero-momentum resonances and low-energy(ϵ≈ 0)total transmissions for very large barriers.
The upper(Dirac)and lower(LM)subplots in Fig.2 show the transmission coefficient corresponding to the same reduced masses and potential parameters,but the methods are different.The Woods–Saxon parameters ared=0.01,V0=3µc2,µ=1,a=1.Note that the potential strength is much stronger than that in Fig.1.The Dirac mass in the upper subplot isµ.The individual masses in the lower subplot are defined byµand the large massm1=3µ,3.7µ,andm1=100µ.The upper subplot is the result from the Dirac equation in(1+1)relativistic dimensions.[14−16]In the LM approximationm1=100µ(dashed-dotted curve),m1=3.7µ(solid curve),andm1=3µ(dashed curve).The best lowenergy similarity of the transmission coefficients of the upper and lower subplots in Fig.2 is form1=3.7µ(solid curve)in this case.The other mass combinations show completely different low-energy dependences.For equal masses(m1=2µ,not shown)large transmissions have not been found in the present investigation.

Fig.3 GS(upper subplot)and LM(lower subplot)computations of T as function of ϵ/V0for three mass combinations each,where d=0.01,V0=3µc2,µ =1,a=1.The continuous(black)curves are nice fits to the Dirac results from Fig.2.The “nice- fit” GS curve corresponds to m1=11µ,and the “nice- fit” LM curve corresponds to m1=3.7µ.
Figure 3 compares GS-and LM-calculations for the Woods–Saxon parametersd=0.01,V0=3µc2,µ=1,a=1.Of three mass combinations each,nice fits to Dirac results are obtained form1=11µ(upper subplot,solid curve)from the GS equation,andm1=3.7µ(lower subplot,solid curve also in Fig.2)from the LM equation.Form1=100µ(dashed-dotted curves)both GS-and LM-results show double peaks at low-energies.Form1=3µ(dashed curves)the GS-method(upper subplot)predicts no transmission peak at threshold energies,while the LM-method predicts some enhanced transmission.
Note that the Dirac results agree approximately with a light-heavy mass(almost single-mass)combination(GS and LM)only at higher energies,above the potential top energy.
6 Conclusion
The local momentum (LM)and the generalized Schrödinger(GS)approximations are numerically compared.Both approximations assume negligible variations in the potential.A Woods–Saxon barrier with parameters close to a rectangular shape is studied in some detail.The LM-approximation provides exact results within the semirelativistic two-body framework for rectangular barrier interactions in(1+1)dimensions,but the GS-approximation provides almost the same results.
This study suggests that GS/LM-approximations are numerically similar for weak potential strengths and a wide range of scattering energies. For very strong interactions,the study shows similarities between LM/GS and Dirac results at energies above the barrier maximum.However,the Dirac-“best- fit” (LM/GS)mass combinations are not the same.
The surface thickness parameterdseems to make LM,GS and non-relativistic results numerically closer to each other asdincreases.This is observed in Table 4 for the over-barrier energy region(ϵ>V0),whereT∼ 1(with very small oscillations).
For barrier widths comparable with the Compton length(a≈1)the Dirac results do not agree with results from SRQ “light-heavy” mass combinations.The strongest difference between the Dirac and SRQ results is for equal masses,in which case SRQ results do not indicate any tunneling at low scattering energies,and therefore no large low-energy transmissions.
“Super-strong” interactions forV0−ϵ>2µc2seem speculative and not fully understood.The more important to compare these results with quantum field theory.Single-particle Dirac results,pointed out by Alhaidari et al.,[14]Thomson[15]and others,indicate total transmission at low(non-relativistic)scattering energies.For equal masses the present study indicates non-existence of large low-energy transmissions.
References
[1]S.M.Ikhdair and R.Sever,IC/92/186(INTERNAL REPORT)(1994);S.M.Ikhdair and R.Sever,Int.J.Mod.Phys.E 17(2008)1107;S.M.Ikhdair and R.Sever,Int.J.Mod.Phys.A 20(2005)16509.
[2]W.Lucha and F.F.Schöberl,Int.J.Mod.Phys.A 17(2002)2233;W.Lucha and F.F.Schöberl,Int.J.Mod.Phys.A 15(2000)3221;W.Lucha and F.F.Schöberl,Int.J.Mod.Phys.A 14(1999)2309;W.Lucha and F.F.Schöberl,Fizika B 8(1999)193;W.Lucha and F.F.Schöberl,Phys.Rev.A 60(1999)5091;W.Lucha and F.F.Schöberl,Phys.Rev.A 54(1996)3790;W.Lucha and F.F.Schöberl,Phys.Rev.D 50(1994)5443;W.Lucha and F.F.Schöberl,Phys.Rev.D 50(1994)5443.
[3]S.Hassanabadia,M.Ghominejada,S.Zarrinkamarb,and H.Hassanabadi,Chin.Phys.B 22(2013)060303;S.Hassanabadi and A.A.Rajabi,Mod.Phys.Lett.A 27(2012)1250057;S.Zarrinkamar,A.A.Rajabi,H.Hassanabadi,and H.Rahimov,Phys.Scr.84(2011)065008;S.Zarrinkamar,A.A.Rajabi,and H.Hassanabadi,Few-Body Sys.52(2011)165.
[4]S.Hassanabadia,M.Ghominejada,and K.E.Thylwe,Commun.Theor.Phys.63(2015)423.
[5]K.E.Thylwe,O.J.Oluwadare,and K.J.Oyewumi,Commun.Theor.Phys.66(2016)389.
[6]I.J.Nickisch,B.Durand,and L.Durand,Phys.Rev.D 25(1982)2312;I.J.Nickisch,B.Durand,and L.Durand,Phys.Rev.D 30(1984)1904.
[7]S.J.Wallace,Phys.Rev.Lett.87(2001)180401.
[8]J.Bijtebier and J.Broekaert,Nuovo Cimento A 105(1992)351.
[9]R.Arshansky and L.P.Horwitz,J.Math.Phys.30(1989)213.
[10]N.F.Mott and H.S.W.Massey,The Theory of Atomic Collisions,Oxford University Press,Cambridge,Ch.2(1965).
[11]K.E.Thylwe,J.Phys.A:Math.Gen.38(2005)235.
[12]W.E.Milne,Phys.Rev.35(1930)863;H.A.Wilson,Phys.Rev.35(1930)948;H.A.Young,Phys.Rev.38(1931)1612;H.A.Young,Phys.Rev.39(1932)455;J.A.Wheeler,Phys.Rev.52(1937)1123.
[13]H.J.Korsch and H.Laurent J.Phys.B 14(1981)4213.
[14]A.D.Alhaidari,H.Bahlouli,Y.Benabderahmane,and A.Jellal,Phys.Rev.A 86(2012)052113.
[15]M.J.Thomson and B.H.J.McKellar,Am.J.Phys.59(1991)340.
 Communications in Theoretical Physics2017年6期
Communications in Theoretical Physics2017年6期
- Communications in Theoretical Physics的其它文章
- A Pair of Resonance Stripe Solitons and Lump Solutions to a Reduced(3+1)-Dimensional Nonlinear Evolution Equation∗
- New Patterns of the Two-Dimensional Rogue Waves:(2+1)-Dimensional Maccari System∗
- Coherent-State Approach for Majorana Representation∗
- Exhibition of Monogamy Relations between Entropic Non-contextuality Inequalities∗
- Quantum Coherence Quantifiers Based on R´enyi α-Relative Entropy∗
- CRE Solvability,Nonlocal Symmetry and Exact Interaction Solutions of the Fifth-Order Modi fied Korteweg-de Vries Equation∗
