一种加速搜索函数极值的剪枝方法
卢伟荣,张磊
(中山大学数学学院,广州 510275)
一种加速搜索函数极值的剪枝方法
卢伟荣,张磊
(中山大学数学学院,广州 510275)
函数的极值求解问题是实际应用中有许多优化问题的最基本的问题,大多数模型的优化问题最终都转化为目标函数的极值问题,如最大似然估计和最小二乘估计。在极值问题的数值解法中,遍历搜索可用于函数的高精度极值求解问题,但其时间复杂度非常高;为解决遍历搜索时间过长的问题,随机搜索方法被引入,如遗传算法和模拟褪火算法,而遗传算法极不稳定不适合大数据下智能问题的复杂目标函数的极值搜索。结合遍历搜索和随机搜索,设计一种基于二进制编码的搜索树,并引入基于模拟退火思想的随机剪枝算法,在保证模型精度的基础上对搜索树进行剪枝。在实验环节使用多种形态的函数进行效用分析,说明其在精度和稳定性及时间效用方面的优势。
极值求解;遍历搜索;模拟退火;数值解法
0 引言
在科学技术的各个领域,通常会对所处理的实际问题进行抽象、简化,进而建立数学模型。其中,函数的极值求解对应了一类常见的实际问题,针对处理在一定条件下,如何实现收益最大,或者成本最低等问题。另外,函数的极值求解问题是实际应用中有许多优化问题的最基本的问题,大多数模型的优化问题最终都转化为目标函数的极值问题,如最大似然估计和最小二乘估计。
根据求解方法的不同,函数极值求解可分为以下两类,精确解法和数值解法。极值模型的精确解一般通过基于导数方法得到满足条件的约束方程,但在实际应用中,往往需要面对目标函数f不可微,或者其基于导数的约束方程难以求解到的问题。相对而言,大部分数值解法,如黄金分割搜索、二次插值法、各种搜索算法及各种迭代法等,仅依赖于目标函数在某些点上的取值,在实际应用中,适用范围更加广泛[1-2]。
遍历搜索,是一种基本且易于理解的数值解法,可用于高精度的函数极值求解。通过对变量区间进行不断地迭代细分,遍历各区间寻找函数最值的近似。该方法有以下两个优点,适用范围广(仅需知道函数值,无可微或连续要求)和全局性强(不易限于局部最优),但运行时间过长的问题限制了该方法在实际中的应用。
针对上述情况,本文设计了一种独特的搜索流程,即一种基于二进制编码树的搜索方法,可设计出深度搜索和广度搜索流程,还可以灵活地进行剪枝以加速寻优进程。本文将基于模拟退火的思想,对搜索树进行剪枝,在保证模型精度的基础上,实现算法时间的优化。最后,将介绍该模型在多元函数上的推广。
1 方法设计和相关理论
1.1 数轴的区间划分与数的二进制表示
假设已通过变换x=(b-a)*x'+a将函数的定义域从[a,b]映射到[0,1],其中a〈b且a,b∈R,不失一般性将函数记为:

令a0=0,b0=1,对∀r∈[0,1],下面将不断二等分r所在的区间:二等分区间[a0,b0],则必有一子区间包含实数r,记该区间为[a1,b1];二等分区间[a1,b1],则必有一子区间包含实数r,记该区间为[a1,b1],…,如图1所示,继续下去,可得到一个区间长度不断减半的闭区间序列{[an,bn]}。

图1 区间套{[an,bn]}的构建
因为:

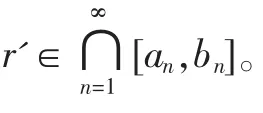
下面追踪区间套的构建过程产生一串与实数r相关的二进制数x[1]…x[k]:第i次二等分区间时,若实数r落入左子区间,则取x[i]=0;若实数r落入右子区间,则取x[i]=1,i=1~k。
可见对∀x∈[0,1],都可按上述方法产生一串二进制数x[1]…x[k],其中k为细分步数。定义实数x的逼近公式为:

可证明,通过上述方法可产生逼近函数定义域内的任意实数的二进制表示0.x[1]x[2]x[k]2,其中k为细分步数,且其误差不大于w[k]=。这里之所以通过追踪区间套的构建过程产生一串与实数r相关的二进制数x[1]…x[k],是为了下一节能够直观分析搜索树的构造。
1.2 搜索树的设计
搜索算法搜索最优解的本质是由初始并非极值点的数产生一个点列,使该点列能够逼近极值点,如下山法将沿函数的负梯度方向产生点列,顺序搜索算法则通过按一定的步长来产生点列,随机搜索算法则通过随机方式来产生点列,不同的搜索算法决定了如何由一个初始点产生下一个点。本文的搜索算法的搜索流程将采用基于解空间树的回溯法,使用回溯法的核心问题是如何将问题的解表示成解空间树,以及如何通过剪枝来提高效率。
下面给出解空间树的构造方法:前一节给出了通过追踪区间套的构建过程产生一串与实数r相关的二进制数x[1]…x[k],第i次二等分区间时,若实数r落入左子区间,则取x[i]=0;若实数r落入右子区间,则取x [i]=1;若我们用左子树追踪左半区间的细分过程,用右子树追踪右半区间的细分过程,则追踪区间套的构建过程产生一棵二叉树,每个点唯一落入一个节点中,而且搜索路径的分枝值将得到由(2)式确定的一个与结点对应的值值,所有这些值构成了侯选的最值,当K足够大时这些侯选值可以逼近定义域中的任意点,因此这种二叉树可以做为解空间树。
由公式(2)的定义可知,x[i],i=1,2,…,k可能的取值为0或者1,因此解空间树是图2所示的满二叉树,在特定精度下可以对每个可能的取值进行试探。如图2所示,对于第i层的结点,x[i]的取值为0时搜索其左子树,相当于搜索左半区间;x[i]的取值为1时则搜索其右子树,相当于搜索左半区间;可见随着树的逐层展开将对定义域进行了更精细的划分[4]。
图2给出了解空间的搜索树结构:其中标注了任何一个节点所对应区间的左端点值的二进制表示,当我们用区间端点值近似表示区间中的任意值时其误差为,i=1~k为节点所在的深度,当我们搜索的深度足够大时,该误差可以控制到任意小;因此当我们用这些值做为搜索最值的侯选点时,不失一般性可以保证结果的有效性。由此可得我们可以通过所要求的精度来控制树的深度:关于k的取值问题,在给定模型截断误差ε的基础上,k通过以下方式定义:


图2 解空间的搜索树结构
1.3 引入模拟退火思想的剪枝算法
回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索,其用于求最小值递归实现的伪代码如下:

上述代码中if(constraint(t)&&bound(t))backtrack(t+1)表示在递归搜索各棵子树之前要有解的可行性测试和界限测试,它们构成了剪枝条件,针对不同的应用设计剪枝条件是用好回溯法的极大挑战。在本文探讨的搜索函数极大(小)值的应用中,可行性测试比较容易表达,因为一个特定的值是否被选择是个简单测试问题;界限测试则非常核心和难以刻画,因为界限测试要回答当前子树是否存在潜在最优解的问题,相当于要回答最优解是否会落入某个区间之中,这肯定是没有一般表达的。本文引入模拟退火算法来设计一种依概率剪枝条件。
模拟退火算法(Simulated Annealing,SA)是一种模拟物理学中固体退火过程的随机优化算法,于1983年由Kirkpatrick S,Jr G C,Vecchi M P等人[5]设计提出并应用于组合优化领域。该算法在搜索最优解的过程中引入随机因素,以一定概率接受一个不优于当前解的解,通过这种随时间而变化并且最终趋于零的概率突变性,能一定程度地避免陷入局部最优,具有渐进收敛性[6]。
在模拟退火算法中,判断是否接受新解的依据是Metropolis准则。不失一般性,假设我们要求最小值,假定问题的当前解为S0,新解为S1,C(S)为目标函数。若C(S1)〈C(S0),则接受S1作为新的当前解;若C(S1)≥C(S0),则以概率p接受S1作为新的当前解。概率p的定义如下:

其中,T代表当前温度,每个温度在进行若干次判断迭代后会逐渐减少,并最终趋于零。
在本文的函数求解模型中,将基于模拟退火算法的思想,对上小节的遍历搜索进行改进。引入模拟退火算法思想的剪枝,是指搜索当前区间对应的子树时,新产生的分点作为新解与当前解进行Metropolis准则测试,拒绝了新解则被拒绝的分点所在子区间对应的子树不用搜索,即对子树进行了剪枝,从而节省了用于搜索一个子区间的时间,这也是为何剪枝条件设计是提高搜索效率的原因。由于模拟退火算法具有随机性,为保证模型结果的稳定性,我们将从第k0+1层开始,对满二叉树进行剪枝,经过大量实验得到k0=×k可满足大多数应用。k由公式(3)确定,这样保证了我们所拒绝搜索的子区间是可以控制它们的长度的。
关于k0的确定问题的探讨:当k0=1时算法退化为模拟退火算法,过于强调随机机制从而造成求解的不稳定性;当k0=k时算法退化为穷举搜索算法,从而增加了时间复杂度。k0的选取主要考虑以下两个方面。一方面,为保证模型结果的稳定性,k0的取值不宜过小,若选取了一个较小的k0值,则模型则会很快进入剪枝阶段,对于高频震荡型函数易陷入局部最小值。另一方面,k0的取值不宜过大,若选取了一个较大的k0值,将面临模型运行时间过长的问题。
可见本文的算法是先进性不剪枝的确定搜索,保证搜索不会遗漏地进入每一个长度为,i=1~k0的区间,在进入到长度为(i大于等于k0)的区间进行更精细搜索时才进行随机剪枝,以一定的概率跳过对更小区间的搜索,能够兼顾精度和效率。
2 用本文方法求函数极值的算法实现流程
经过前面的准备工作之后,下面开始介绍函数极值求解模型的构建流程。本小节将主要介绍一元函数的极值求解,该问题在多元函数上的推广将在后面介绍。现假定实际问题抽象得到的模型函数记为:

本文算法主要由以下两个阶段构成:定位阶段和剪枝阶段。
定位阶段是指在深度小于k0时所进行的不剪枝的确定性搜索。图3展示了该算法在定位阶段的操作流程,二叉树的根结点代表全区间,每次二分一个区间,左半区间对应左子树,右半区间对应右子树,其中括号中给出了区间左端点的值的二进制表示和十进制表示,因此搜寻每个数的过程对应该二叉树中的一条路径,而回索法则通过深度优先的方式遍历各路经从而实现解的搜索。
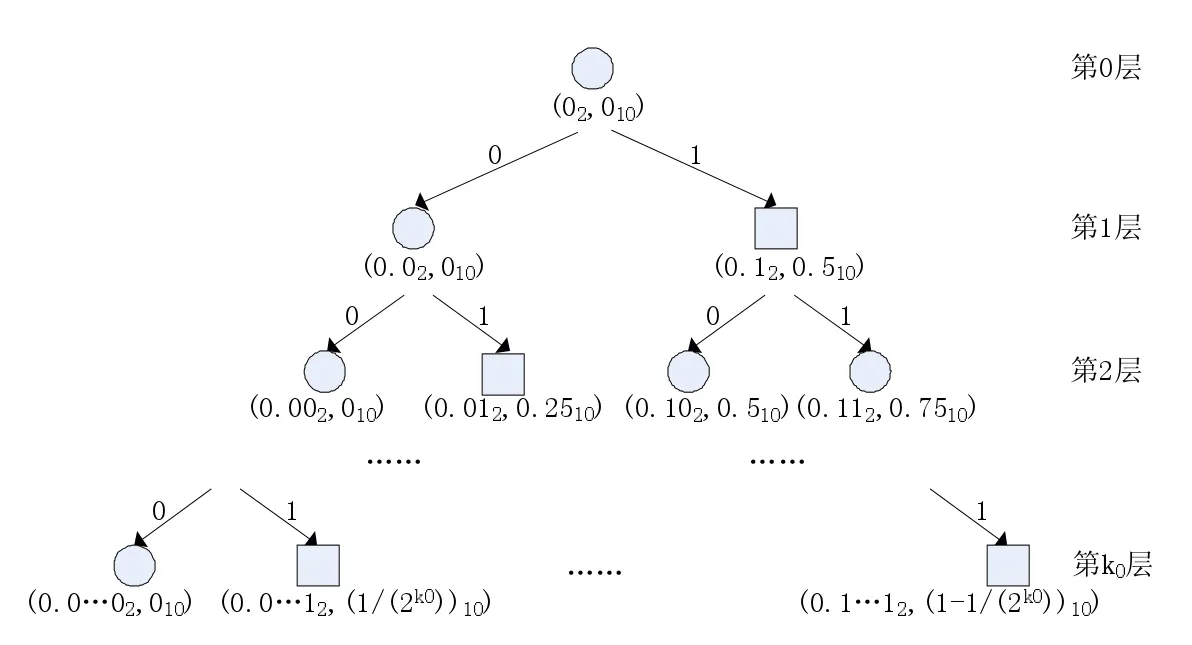
图3 函数极值求解模型的定位阶段
在定位阶段进行深度为k0的深度优先搜索,为降低时间复杂度仅对各结点的右孩子函数值的更新操作,因为左孩子所产生的区间端点并非新的值。在图3中,方型结点将与当前解作函数值大小的比较判断,圆形结点则不进行该操作。
定位操作发生在搜索树的第1至k0层,从第k0+1至k层进行剪枝操作,其中k0=×k,k由公式(3)确定。也就是说在定位阶段是对深度为k0的搜索树进行的深度优先搜索,在这个过程中不进行随机剪枝可有效保证解的精度。但是,如果整棵树的搜索过程中都不进行剪枝,则算法复杂度太高,因此从第k0+1至k层进行剪枝操作,也就是说在深度大于k0子树中搜索时则引入1.3节介绍的剪枝操作,因此下面的过程针对当前要进行剪枝操作的任意一棵深度大于k0子树。
在剪枝阶段,同样的道理仅对各结点的右孩子进行操作。剪枝规则定义如下:
(1)若f(x1)〈f(xmin),则接受x1为新的极小值点,不进行剪枝操作,继续对子树的深度优先搜索。

①若p>ξ,则不进行剪枝操作;
②若p≤ξ,则进行剪枝操作。
其中,xmin为当前极小值点,x1为待判断的新点,f为目标函数,i为x1对应结点在满二叉树中的层数,用w[i]=作为模拟退火算法的温度值,这也是本文经大量实验得出的有效选择。ξ∈[0,1]为随机数。图4展示了该模型在剪枝阶段的操作流程。

图4 函数极值求解模型的剪枝阶段
上面的流程是针对一元函数设计的,下面的探讨将针对多元函数极值求解进行推广。为便于理解,以下将以二元函数为例,对于三元或以上的函数,可以通过相似的步骤实现。现假定实际问题抽象得到的模型函数记为

其中,D={(x1,x2)∈R2|0≤x1≤1,0≤x2≤1}。
为达到模型精度要求,由公式(3)求得k值后,将构建一棵层数为2k的满二叉树。模型同样由两个阶段构成:定位阶段和剪枝阶段。
在定位阶段,先对定义域各端点作比较,取其最小者作为初始极小值点,在二元函数中,有以下四个端点(0,0)、(0,1)、(1,0)和(1,1)。然后,在对满二叉树搜索的过程中,以两层为单位,在奇数层对x1的取值进行试探,在偶数层对x2的取值进行试探,如图5所示,结点下括号内左数值代表变量x1的取值(二进制表示);右数值代表变量x2的取值(二进制表示)。同样的,仅各层结点的右孩子进行比较判断。
定位操作发生在搜索树的第1至k0层,从第k0+1至k层进行剪枝操作,其中k0=×2×k。在剪枝阶段,剪枝规则与一元函数相似,这里不再赘述。
3 实证分析
3.1 实验所选函数简介
在该小节,主要介绍用于测试本文算法效果的各个实验函数。为确保算法的泛化能力,实验函数将尽可能地涵盖不同的类型。如表1所示,在一元函数极值求解模型中,有六个函数用于测试,函数类型与函数特点不尽相同,图6为各函数对应图像。
对于多元函数的实验测试,这里选用了一个二元函数,其定义如下:
统计并记录两组患者的血糖水平,包括空腹血糖、餐后2 h血糖水平、不良妊娠结果。其中不良妊娠结果包括早产、死产、感染、剖宫产。

其对于函数图像如下:

图5 二元函数极值求解模型的定位阶段
3.2 算法效用分析
在一元函数极值求解的实验中,取精度ε1= 0.0000001,根据公式(3)计算可知,k1=24。在二元函数的实验中,ε2=0.0001,k2=14。
(1)稳定性分析
前面分析中提到随机搜索是一种不稳定的算法,因此下面的实验对比本文方法和模拟退火算法的稳定性在实验环节,各算法将在不同函数上各运行10次,观测各次求解得到的极小值是否一致,以本文算法在y=sinx+cos函数上的运行结果为例,通过表2可知,10次运行求得的极小值点相同,具有较强的稳定性。在其余5个一元函数上,该算法均表现十分稳定。
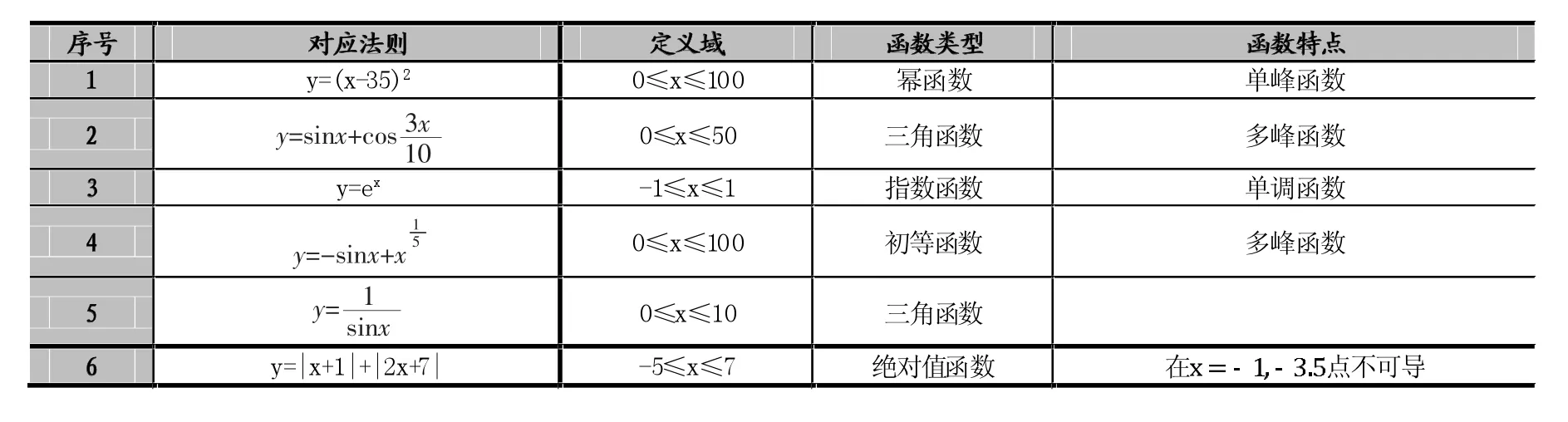
表1 实验所选一元函数的简要介绍

图6 本实验涉及的一元函数图像

图7 本实验涉及的二元函数图像
需要注意的是,稳定性与k0的选取有关,若k0的值过小,则有可能出现极小值点不同的情况,影响模型精度。
表2 本文模型在y=sinx+cos函数上的运行结果

表2 本文模型在y=sinx+cos函数上的运行结果
(2)精度分析与运行时间分析
搜索算法的时间复杂度取决于其侯选搜索空间的设定,为了能对比不同搜索算法的时间复杂度,我们约定用各算法完成对相同搜索空间的搜索时间,本实验中对一元函数取精度ε1=0.0000001,根据公式(3)计算可知,树的深度k1=24。在二元函数的实验中,取ε1= 0.0001,树的深度k1=14。
在该环节,将取10次实验的众数用于精度的考察,实验时间均数用于运行时间的考察。对于一元函数,在减低实验耗时上,本文算法优于遍历搜索算法,仅需其约10%的运行时间,六个函数中,最短为后者的7.87%,最长为13.14%,与模拟退火算法相比则两者相近,本文算法依然有一定优势。在精度上,本文算法均有很好的表现。表3给出了对比结果。
可见本文算法能用更短的时间找到搜索空间中的最小值,本文设计的剪枝策略能够在不影响精度的情行下降低时间复杂度,是一种能兼顾精度稳定性和效率的有效方法。
4 结语
本文在遍历搜索算法的基础上,基于模拟退火的思想,通过对搜索树进行剪枝,在保证模型精度的同时,解决其运行时间过长的问题。本文结合遍历搜索和随机搜索,设计了一种基于二进制编码的搜索树,并引入了基于模拟退火思想的随机剪枝算法,在保证精度的基础上对搜索树进行剪枝,从而可以兼顾精度和效率。该算法适用范围广,全局性强,能有效处理高精度函数极值求解问题,能有效推广至多元函数。算法的改进方向为如何使得该模型能更好地处理高频震荡函数,进一步地,考虑实现模型的并行化,更大程度地优化运行时间。

表3 三种方法在精度与耗时上的比较
[1]Brent,Richard.P.,Algorithms for Minimization Without Derivatives,Prentice-Hall,Englewood Cliffs,New Jersey,1973.
[2]Forsythe,G.E.,M.A.Malcolm,C.B.Moler.Computer Methods for Mathematical Computations,Prentice-Hall,1976.
[3]邓东皋,尹小玲.数学分析简明教程.上册[M].高等教育出版社,1999.
[4]王晓东.计算机算法设计与分析[M].电子工业出版社,2012.
[5]Kirkpatrick S,Jr G C,Vecchi M P.Optimization by Simulated Annealing[J].Science,1983,220(4598):671-80.
[6]Van Laarhoven P J M,Aarts E H L.Simulated Annealing:Theory and Applications[J],1987,37(1):108-111.
A Pruning Method for Accelerating to Search Function Extremum
LU Wei-rong,ZHANG Lei
(School of Mathematics,Sun Yat-sen University,Guangzhou 510275)
There are many optimization problems in practical applications that can be abstracted and simplified to search the function extremum. However,the problem that the function is not differentiable or its derivative is difficult to compute limits the use of exact methods.The traversal search,one of the numerical methods,can be used to search the high-precision extremum.To solve its problem of running too long,the search tree will be pruned based on the idea of simulated annealing in the case of ensuring the model accuracy.The model can be extended to multivariate function,which has the advantages of wide applicability and strong global character.To ensure the practical significance of the model,various types of functions will be used to test in the experimental part.
Function Extremum Search;Traversal Search;Simulated Annealing;Numerical Methods
1007-1423(2017)11-0003-07
10.3969/j.issn.1007-1423.2017.11.001
卢伟荣(1993-),男,广东东莞人,硕士生,研究方向为人工智能
2017-01-10
2017-03-10
张磊(1964-),女,湖北罗田人,副教授,研究方向为数据分析

