慎用“特殊点法”,解决线性规划问题

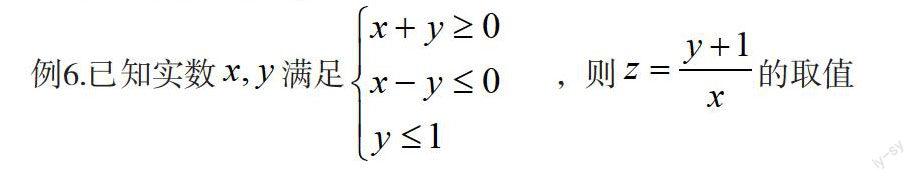
摘 要:线性规划是通过数形结合方法来解决日常生活实践中的最优化问题的一种数学模型,其核心是运用数形结合的思想方法求目标函数的最值问题(其中有一个重要的过程就是可行域的作法)具有很强的现实意义。在高考中属于必考内容,多以选择填空题的形式出现。这部分內容在学生已经学习了函数的应用、不等式的解法,也学习了运用二元一次不等式(组)刻画平面区域,具备了相关知识的储备。
关键词:线性规划;数形结合;最值问题;特殊点法
在线性约束条件下,寻求目标函数的最值问题,称为“线性规划问题”。一般采用“图解法”:先作出约束条件表示的平面区域,而后根据“目标函数”的特征,必要时结合其“几何意义”进行求解。因为要“作图”,故解题速度明显受到制约.因此,在实际练习或考试中,很多学生热衷于使用“特殊点法”,以求避开作图,快速解出答案。如:
例1、已知点在不等式组表示的
平面区域上运动,则的取值范围是( )。
(A)[-2,-1] (B)[-2,1]
(C)[-1,2] (D)[1,2]
解法一:常规做法是利用直线的截距解决最值问题
解析:由线性约束条件画出可行域如图1,考虑,把它变形为,这是斜率为1且随z变化的一族平行直线.是直线在y轴上的截距。当直线满足约束条件且经过点(2,0)时,目标函数取得最大值为2;直线经过点(0,1)时,目标函数取得最小值为-1.故选(C).
解法二:很多学生热衷于使用“特殊点法”,以求避开作图,快速解出答案。
解析:求出三条直线交点,求出三个交点坐标分别为(0,1),(2,1),(2,0),然后再一一代入目标函数,比较可知z=x-y分别在点(0,1),(2,0)取得最小值为—1,最大值为2,求出z=x-y的取值范围为[1,2],更为简单。
点评:解法二即为“特殊点法”,显然较之“图解法”来说,因为避开了作图,大大提升了解题速度.此乃“特殊点法”的最大优点。
线性规划问题的最优解,往往是平面区域的“某个顶点”,由此产生了规划问题的“特殊点法”。这种方法是先求出边界直线的所有交点,再代入目标函数计算结果,比较大小得出答案.当然不能否认这种方法有时候的确很好用,但是也应该看到该解法,受到很多因素限制,缺乏完备理论支撑,可谓“四肢不健全”,因此有“诸多不宜”,会时常失效。
笔者归纳以下几方面不能用“特殊点法”
一、当边界直线的个别交点不在约束条件所表示的平面区域内时,不宜使用“特殊点法”
例2:设变量x,y满足则的最大值为
________
点评:本题不宜用“特殊点法”,原因何在? 求出三条直线的交点分别为(0,1),(0,-1),(1,0),代入目标函数比较可知在点(0,1)得到最大值2.可是利用图解法作出不等式所表示的平面区域,你就会发现:此时点(0,1)不在平面区域内,换句话说,它不可能是最优解了,所以不宜使用“特殊点法”。
二、当约束条件中含有非线性条件时,不宜使用“特殊点法”
例3.已知实数满足,则的最
大值是________
点评:本题不宜用“特殊点法”,原因何在?因为约束条件中含有非线性条件二元二次不等式,画出平面区域可知当目标函数取得最大值时,直线与圆相切于第一象限.所以目标函数取到最大值的最优解并不是边界直线的交点.因此,不宜用“特殊点法”。
三、当目标函数是非线性时,不宜使用“特殊点法”
例4.已知实数满足,则的最小
值是________
点评:本题不宜用“特殊点法”,原因何在?因为目标函数是非线性的,其几何意义为:平面区域内的点到原点的距离的平方.画出平面区域,过原点作直线的垂线,可知当点为垂足时,目标函数取得最小值时,只须求出原点到直线的距离,再平方可得目
标函数的最值为.由此可见目标函数取到最小值的最优解并不是边界直线的交点.于是用特殊法就会出错!
例5.已知实数满足,则z=xy的最
大值是________
点评:本题不宜用“特殊点法”,原因何在?因为目标函数是非线性的,出现“乘积”形式,目标函数z=xy可转化
为,表示双曲线.画出平面区域,当曲线与直线相切于点(4,4)时,目标函数z=xy取得最大值16.由此可见目标函数取到最大值的最优解并不是边界直线的交点。于是用特殊法就会出错!
四、当出现求目标函数取值范围时,用特殊法很难判断范围,不宜使用“特殊点法”
例6.已知实数满足,则的取值
范围是________
点评:当目标函数形如时,可把z看作是动点
与定点连线的斜率,这样目标函数的最值就转化为PQ连线斜率的最值。
本题不宜用“特殊点法”,原因何在?因为目标函数是非
线性的,目标函数表示平面区域上的点与点(0,-1)连线的斜率,求出边界直线的交点(0,0)、
(1,1)、(-1,1),容易知道在点(1,1)、(-1,1)处取到临界值2.-2,但用特殊法容易误认为[-2,
2]而发生错误.画出平面区域,可知取值范围为。
五、实际应用题整点调整法,不宜使用“特殊点法”
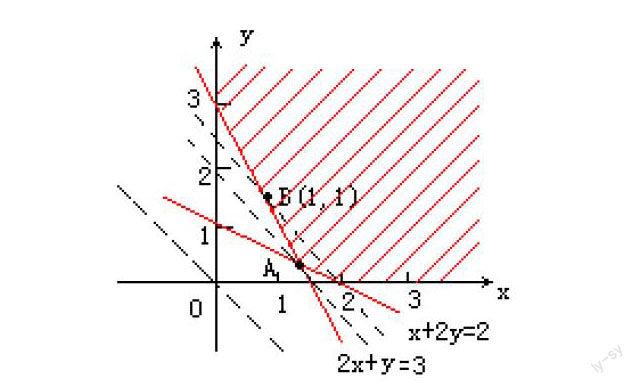
例7.某人承揽一项业务,需做文字标牌2个,绘画标牌3个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小。
点评:本题不宜用“特殊点法”,原因何在? 因为在工程设计、经营管理等活动中,经常会碰到最优化决策的实际问题,而解决此类问题一般以线性规划为其重要的理论基础。然而在实际问题中,最优解(x,y)通常要满足x,y∈N,这种最优解称为整点最优解,求出来的交点坐标如果不是整数,就不能在端点取得最优解,要画出区域,在求出来的交点处附近找整点最优解。
解:设用甲种规格原料x张,乙种规格原料y张,所用原料的总面积是zm2,目标函数z=3x+2y,
线性约束条件作出可行域.
作一组平行直线3x+2y=t
点A不是整点,A不是最优解.在可行域内的整点中,点B(1,1)使z取得最小值.z最小=3×1+2×1=5,
答:用甲种规格的原料1张,乙种原料的原料1张,可使所用原料的总面积最小为5m2.
从以上几种情况可发现:用特殊点法解规划问题,的确有“诸多不宜”,做对答案也带有一些“运气”成分.因此我们在遇到“线性规划”的题目时,还是要以“图解法”为根本,从提高作图的速度与规范性方面加强训练才是正道.而对于“特殊点法”要慎重选择,因为本就不难的题型,只为追求解题速度而增加做题风险,到头来反而容易落个“得不偿失”。
作者简介
黄春华,女,福建南安,中学高级,本科学历。
(作者单位:福建南安市诗山中学)

