Invariants-based shortcuts for fast generating Greenberger-Horne-Zeilinger state among three superconducting qubits∗
Jing Xu(徐晶),Lin Yu(于琳),Jin-Lei Wu(吴金雷),and Xin Ji(计新)
Department of Physics,College of Science,Yanbian University,Yanji 133002,China
Invariants-based shortcuts for fast generating Greenberger-Horne-Zeilinger state among three superconducting qubits∗
Jing Xu(徐晶),Lin Yu(于琳),Jin-Lei Wu(吴金雷),and Xin Ji(计新)†
Department of Physics,College of Science,Yanbian University,Yanji 133002,China
As one of the most promising candidates for implementing quantum computers,superconducting qubits(SQs)are adopted for fast generating the Greenberger–Horne–Zeilinger(GHZ)state by using invariants-based shortcuts.Three SQs are separated and connected by two coplanar waveguide resonators(CPWRs)capacitively.The complicated system is skillfully simplified to a three-state system,and a GHZ state among three SQs is fast generated with a very high fidelity and simple driving pulses.Numerical simulations indicate the scheme is insensitive to parameter deviations.Besides,the robustness of the scheme against decoherence is discussed in detail.
Greenberger–Horne–Zeilinger state,superconducting qubits,shortcuts to adiabaticity
1.Introduction
With the rapid development of quantum information processing,the concept of quantum entanglement is increasingly considered to be essential.Generations of entangled states are heavily relied on in many important applications, such as quantum teleportation,[1]quantum communication,[2]quantum secret sharing,[3]fault-tolerant computing,[4,5]and so on.[6]Greenberger–Horne–Zeilinger(GHZ)states are a group of well-known entangled states because they provide a possibility for testing quantum mechanics against local hidden theory without using Bell’s inequality.[7,8]Therefore,various schemes for generating GHZ states have been proposed during the past ten years or more in various physical systems,such as trapped ions systems,[9]photons systems,[1,10]atoms systems,[11]and solid systems.[12]In addition,many schemes for generating GHZ states have been implemented by using superconducting qubits(SQs)in superconducting circuits.[13–17]Compared with other systems,SQ systems possess a natural superiority of scalability for implementing quantum computers.[18–21]Devices of SQs used in quantum computers can be created more easily for large-scale integration and scale with the mature microelectronic technique.Besides, coupling strengths among SQs can be controlled well up to desired values through modulating electromagnetic signals and designing level configurations.In this paper,as one of the most promising candidates for implementing quantum computers,SQs are adopted for fast generating GHZ state.
Stimulated Raman adiabatic passage(STIRAP)is one technique related to adiabatic evolution and has been widely used for robust quantum state transfer.[22–24]STIRAP has also been used to generate GHZ states in cavity quantum electrodynamics.[25–28]In an SQ system,Wu et al.generated n-qubit GHZ states based on STIRAP in 2016.[29]As is well known,however,STIRAP usually requiresa relatively long interaction time for restraining non-adiabatic transitions,which may accumulate decoherence and errors leading to useless dynamics.Therefore,a set of techniques of shortcuts to adia-baticity(STA),which aim to accelerate an adiabatic evolution process,arose at the historic moment.[30–44]Take some of the most recent works as examples;Kang et al.proposed two schemes to speed up adiabatic evolutions by reverse engineering of a Hamiltonian,[42,43]and Chen et al.presented arbitrary quantum state engineering in three-state systems.[44]By using STA,lots of remarkable achievements have been made in quantum information processing.[45–55]Also,many schemes have been proposed for speeding up the generations of GHZ states.[56–61]
Recently,some schemes have been proposed by combining the technique of STA and the SQ system to generate entangled states.For example,Zhang et al.proposed a scheme for fast reparation of the three-qubit GHZ state in 2016;[59]Kang et al.proposed two schemes to fast generate W states in 2016;[62,63]Yu et al.fast generated a W state recently.[64]There are generally two kinds of techniques of STA widely used.One is to construct a Hamiltonian by means of instantaneous eigenstates given,and the other is to chase down the desired instantaneous eigenstates based on the given Hamiltonian.Invariants-based shortcuts we will employ in this paper belong to the second kind.Different from Refs.[56]–[59]using the first kind of technique,the scheme needs to neither interpolate the system Hamiltonian nor add counter-diabatic driving pulses,but find a pair of suitable Rabi frequencies by constructing a Hermitian invariant of the system.Compared with Refs.[60]and[61]also using the invariants-based short-cuts,apart from advantages of the SQ system,the scheme we proposed has simpler energy level configurations of qubit carriers and fewer driving pulses.
2.Physical model and effective dynamics
The physical model for generating the GHZ state among three SQs is shown in Fig.1.There are three SQs separated by two single-mode coplanar waveguide resonators(CPWRs) capacitively.The three SQs have identical Λ-type level configuration with one upper level|e〉and two lower levels|gL〉and|gR〉.Transitions|e〉1↔|gL〉1of SQ 1 and|e〉2↔|gL〉2of SQ 2 are resonantly coupled to CPWR-L with corresponding coupling strengths λ1,Land λ2,L,respectively.|e〉2↔|gR〉2of SQ 2 and|e〉3↔|gR〉3of SQ 3 are resonantly coupled to CPWR-R with corresponding coupling strengths λ2,Rand λ3,R,respectively.In addition,|e〉1↔|gR〉1of SQ 1 and |e〉3↔|gL〉3of SQ 3 are resonantly driven by two time dependent classical laser fields with corresponding Rabi frequencies ΩR(t)and ΩL(t),respectively.Then,the interaction Hamiltonian of the whole system is(¯h=1):
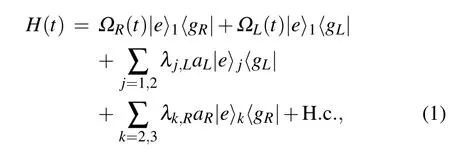
where aL(R)is the annihilation operator of CPWR-L(R).

Fig.1.(color online)The diagrammatic sketch of the SQ system,level configurations,and related transitions of three SQs.
The system initial state is|φ1〉=|gR〉1|gL〉2|gR〉3|0〉L|0〉R, denoting the three SQs in states|gR〉,|gL〉,and|gR〉,respectively,and the two CPWRs both in the vacuum state.The SQ system will evolve in the subspace spanned by

with|1〉L(R)denoting a single photon in CPWR-L(R).Then Hamiltonian(1)can be rewritten as H(t)=Ha−l(t)+Ha−cwith

If we set λ1,L=λ2,L=λ2,R=λ3,R=λ with λ being real,and choose the eigenstates of Ha−c,
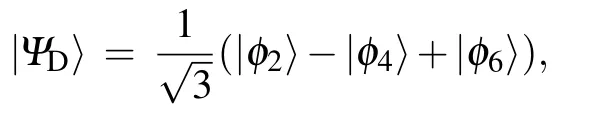

with the corresponding eigenvalues 0,±λ,andas a set of transformations,then Hamiltonian(3)will become
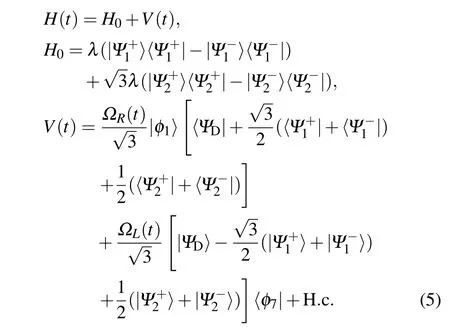
Through performing the unitary transformation U= exp(−i H0t)and disregarding high oscillating terms with the limit condition ΩL(R)(t)≪2λ,Hamiltonian(5)is simplified to an effective Hamiltonian
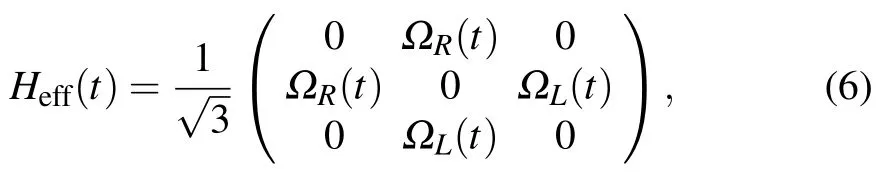
in the subspace{|φ1〉,|ΨD〉,|φ7〉}.The effective Hamiltonian(6)can be viewed as the Hamiltonian of a three-state system,and it will approximatively govern the evolution of the SQ system as long as the limit condition ΩL(R)(t)≪2λ is satisfied very well.
3.Invariants-based shortcuts for fast generating the three-qubit GHZ state
In this section,we show the invariants-based shortcuts for fast generating the three-qubit GHZ state based on the effective Hamiltonian(6).First of all,we give a brief review concerning Lewis–Riesenfeld invariants theory.[65]A time dependent Hermitian invariant I(t)of a quantum system governed by a time-dependent Hamiltonian H(t)satisfies
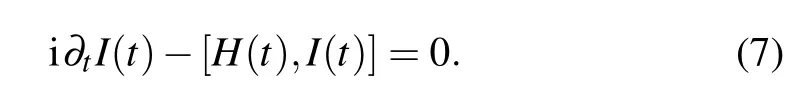
The solution of the time-dependent Schrödinger equation i∂t|Ψ(t)〉=H(t)|Ψ(t)〉can be expressed as a superposition of the instantaneous eigenvectors of I(t)
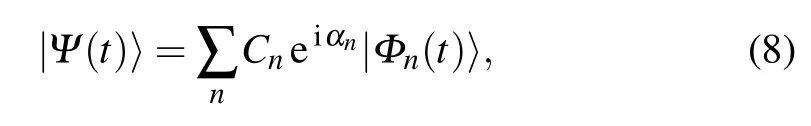
where Cn=〈Φn(0)|φ1〉is the time-independent amplitude,αnis the Lewis–Riesenfeld phase,and|Φn(t)〉is one of the orthogonal eigenvectors of I(t).The Lewis–Riesenfeld phase is expressed by
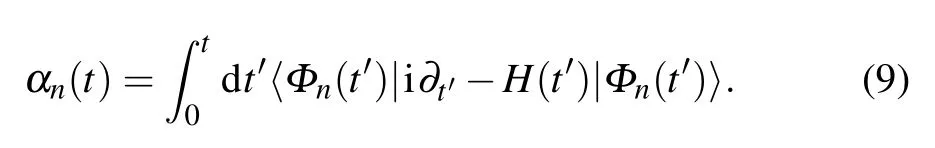
For the effective three-state system with Hamiltonian(6), one of its Hermitian invariants can be chosen as
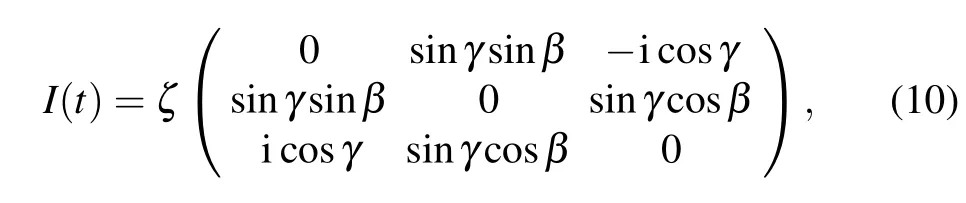
where ζ is an arbitrary constant with frequency unit making I(t)have the dimension of energy.γ and β are two parameters determined later.The eigenvectors of I(t)with the eigenvalues η0=0 and η±=±1 are respectively

In order to insure that I(t)is one of the Hermitian invariants of the effective system,based on Eq.(7),the two Rabi frequencies have to be written as
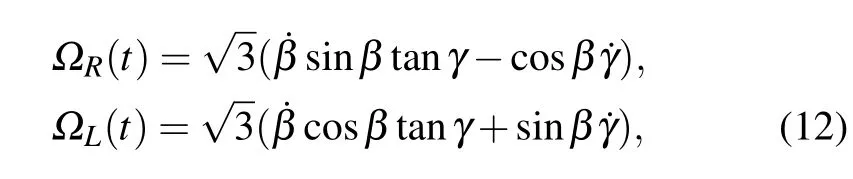
where the dot represents the time derivative.
In order to generate the GHZ state in a relatively easy way,we desire that Hamiltonian(6)could drive the initial state |φ1〉to the target statealong the invariant eigenvector|Φ0(t)〉,which demands

where we have assumed that the scheme starts at t=0 andfinishes at t=tf.In this way,Heff(t)must have the same eigenvectors as I(t)at the two boundary time,which requests [Heff(0),I(0)]=0 and[Heff(tf),I(tf)]=0,i.e.,
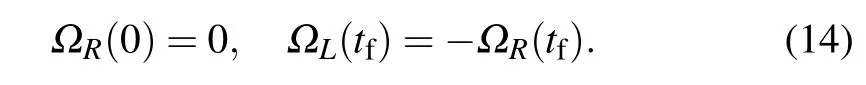
Equations(12)–(14)imply the additional boundary conditions
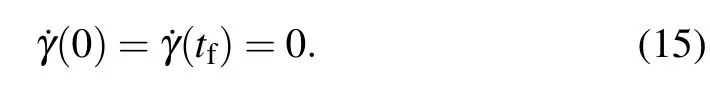
Thus equations(13)–(15)give all the boundary conditions. However,it is worth noticing that the conditions γ(0)=γ(tf)= π/2 cause infinite Rabi frequencies ΩR(t)and ΩL(t),which implies that the evolution|φ1〉→|ΨGHZ〉along|Φ0(t)〉we desired is infeasible.Therefore,we slightly cut down the requirement and replace γ(0)=γ(tf)=π/2 by
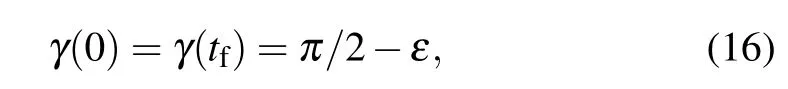
with ε being a time-independent small value.Now the system evolution is not along|Φ0(t)〉any more but along the superpositions of|Φ0(t)〉and|Φ±(t)〉,and the finishing of the desired evolution|φ1〉→|ΨGHZ〉strongly depends on the selection of ε.
Now in order to meet all the boundary conditions,we choose the parameters as
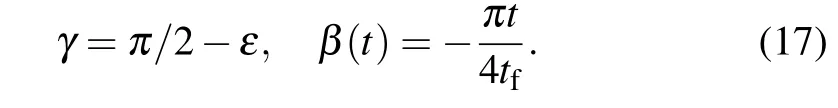
Then we can obtain the Rabi frequencies based on Eq.(12)as
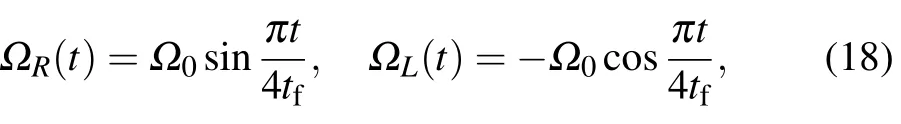

with the Lewis–Riesenfeld phases
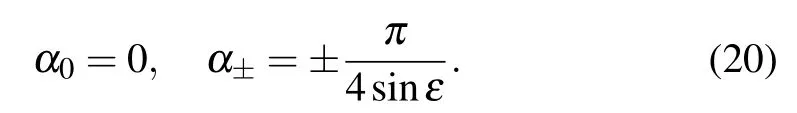
Considering a pair of appropriate Rabi frequencies and thefinal fidelity F(tf)=1,we choose

By the way shown above,we have constructed an invariant based shortcut for fast generating the GHZ state among three SQs.
4.Numerical simulations and discussion
In this section,we perform numerical simulations to show the availability and robustness of the scheme for generating the GHZ state.First of all,for testing that the value ε=0.1253 is right and picking a suitable final time tf,we show a contour plot of the final fidelity versus ε and tfin Fig.2.Obviously,figure 2 shows that the value ε=0.1253 may guarantee a very high final fidelity.Besides,tfalso heavily affects the final fidelity and a larger tfwill give a higher final fidelity.Because Ω0is inversely proportional to tf,a larger tfcan satisfy the limit condition ΩL(R)(t)≪2λ better.
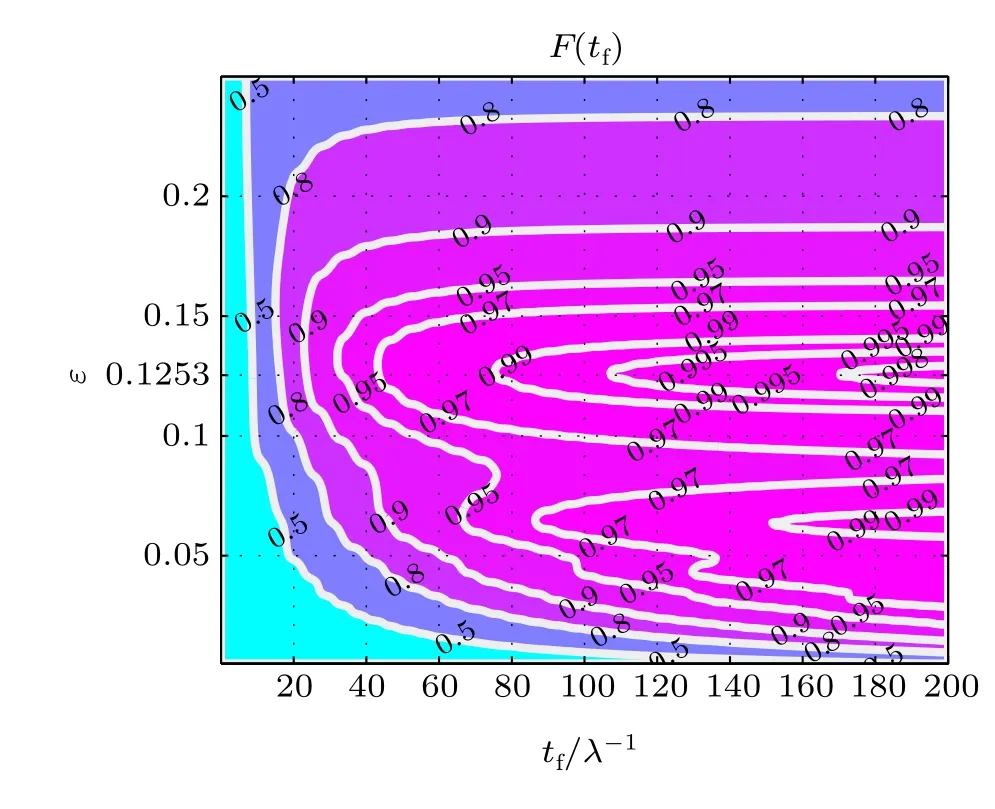
Fig.2.(color online)Contour plot of the final fidelity versus ε and t f.
In order to prove that the scheme we proposed is fast,in Fig.3,we give a comparison between the STA scheme and the STIRAP scheme for the same GHZ state.For the STIRAP scheme,we choose the Rabi frequencies as[26–28]

with two related Gaussian parameters t0=0.14tfand tc= 0.19tf.As we know,the adiabatic criterion in the STIRAP scheme requires either a very long operation time or very large differences among the system eigen energies,[66]and thus the only way to shorten the operation time is enhancing the amplitudewhich requires more physical resources.Besides, as shown by the dotted green line of Fig.3,cannot be too much largerbecause of the limit condition.Numerically speaking,when the operation time is tf=100/λ, the final fidelity of the STA scheme is over 0.94 and the corresponding Ω0≈0.1λ.For the STIRAP scheme,however,when=0.1λ and the final fidelity is up to 0.94,the corresponding operation time is near tf=450/λ,which is 4.5 times of that for the STA scheme.Therefore,the STA scheme we proposed for generating the GHZ state among three SQs is fast. For a relatively high final fidelity and a relatively short operation time,we choose tf=100/λ for following discussions.
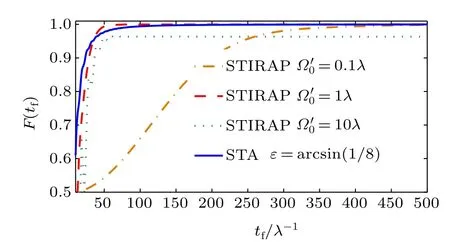
Fig.3.(color online)Comparison between the STA scheme and the STIRAP scheme.

Fig.4.(color online)(a)Time dependence of the fidelity.(b)Time evolution of the populations of|φ1〉,|φ7〉,and excited states.
For exhibiting the availability of the STA scheme,in Fig.4,we plot the time dependence of the fidelity for generating the GHZ state and time evolution of the populations of the states(P1for|φ1〉,P7for|φ7〉,andfor all excited states including SQs excited states|φ2,4,6〉and CPWRs excited states|φ3,5〉).From Fig.4(a),we see that the fidelity gradually increases with the increase of time and reaches near unity at the final time tf=100/λ.Furthermore,figure 4(b) clearly shows that the GHZ state is near perfectly obtained at the final time and other states not involved in the GHZ state are hardly populated during the whole evolution.In a word,the STA scheme we proposed for fast generating the GHZ state among three SQs is quite valid.
Since most control parameters are impossible to be adjusted perfectly in experiment,we consider effects of variations in the control parameters on the final fidelity for the GHZ state generation in the STAscheme.Here we defineδx=x′−x as the deviation of x,where x denotes the ideal value and x′denotes the actual value.In Fig.5,we show the effects of the variations in two primary parameters tfand Ω0on the final fidelity for generating the GHZ state among three SQs.As shown in Fig.5,the STA scheme we proposed is robust against the variations in tfand Ω0,because the final fidelity is beyond 0.985 even when|δtf/tf|=|δΩ0/Ω0|=0.1.

Fig.5.(color online)Effects of variations in control parameters on the final fidelity.
Finally,by taking decoherence caused by SQs energy relaxations,CPWRs photon leakages,and SQs dephasing into account,the evolution of the whole system will be dominated by the master equation
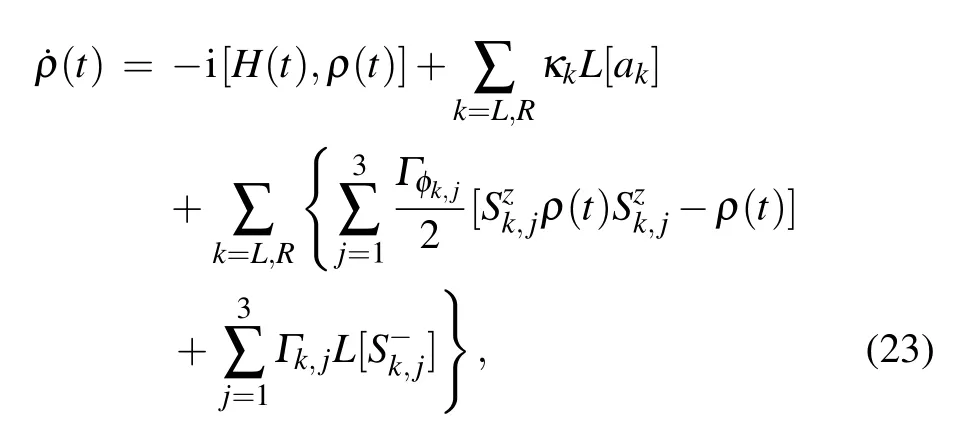
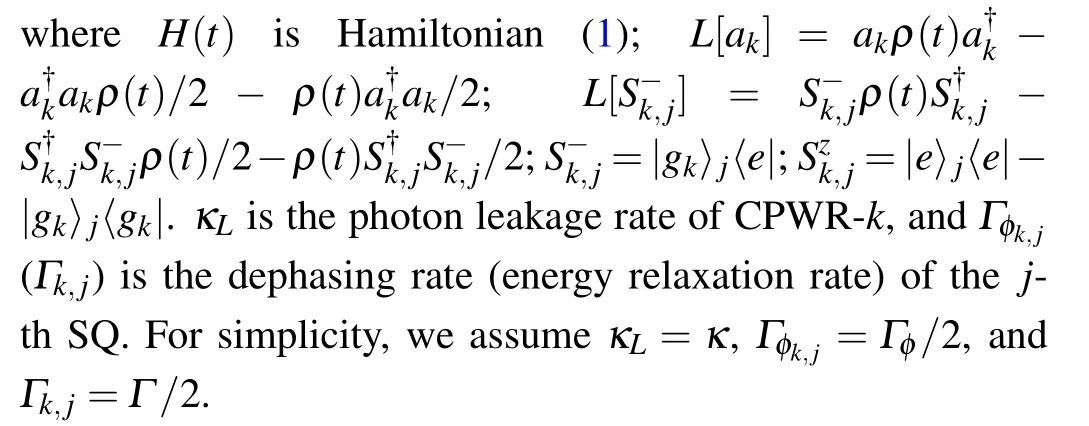
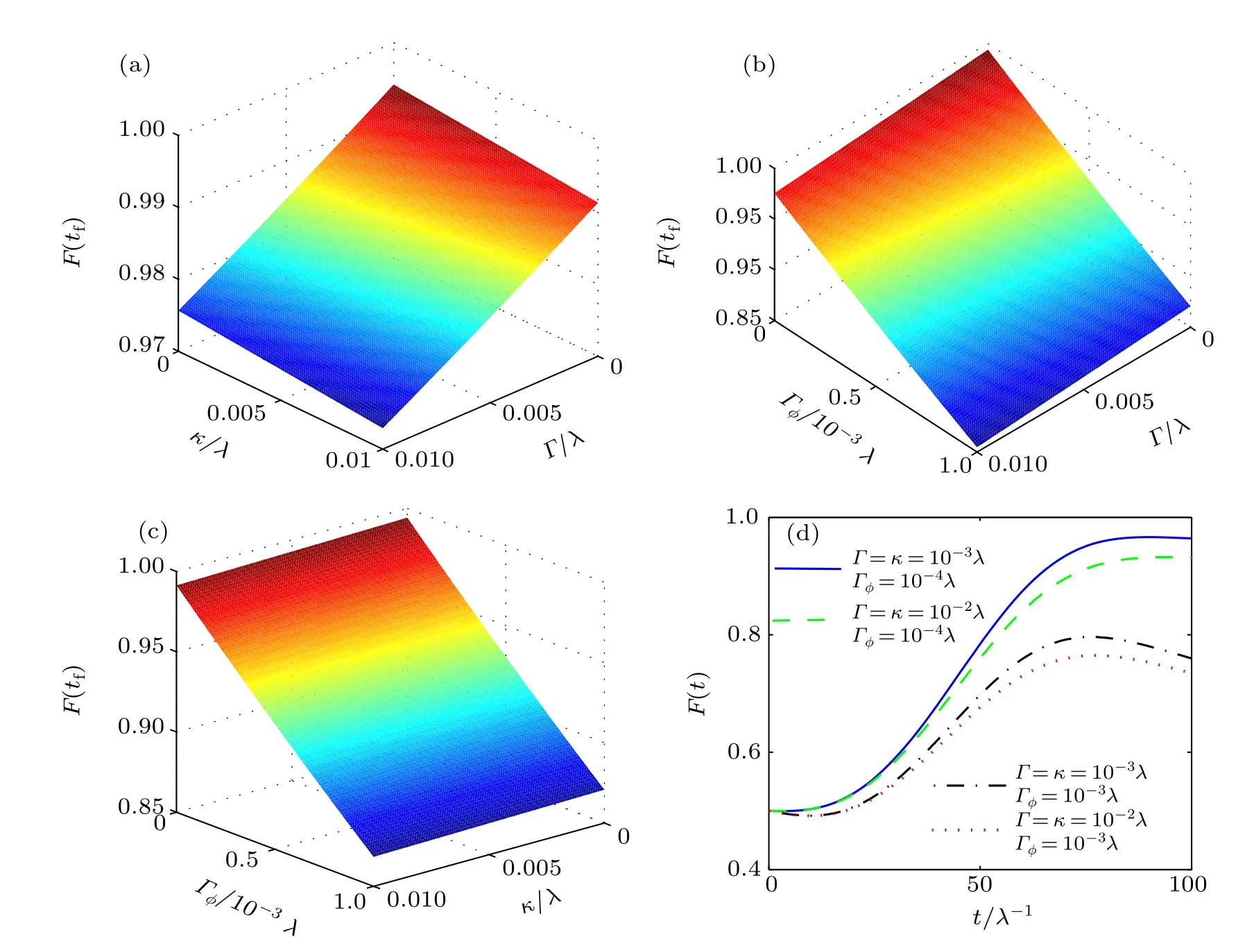
Fig.6.(color online)(a)Final fidelity versus κ/λ and Γ/λ with Γφ=0.(b)Final fidelity versus Γφ/λ and Γ/λ with κ=0.(c)Finalfidelity versus Γφ/λ and κ/λ with Γ=0.(d)Time dependence of the fidelity in the presence of three decoherence factors.
Based on the master equation above,in Figs.6(a)–6(c), we plot the final fidelity versus every two decoherence factors of SQs energy relaxations,CPWRs photon leakages,and SQs dephasing.Set the effects of SQs energy relaxations,CPWRs photon leakages,and SQs dephasing on the final fidelity as EΓ,Eκ,and EΓφ,respectively.From Figs.6(a)–6(c),we can clearly deduce Eκ≪EΓ≪EΓφ,and we can say that compared with EΓφ,EΓand Eκare negligible.Moreover,we also plot the time dependence of the fidelity in the presence of three decoherence factors in Fig.6(d).Through comparing the four curves and the corresponding parameters,we can also deduce that the STA scheme is sensitive to the decoherence caused by SQs dephasing.However,the scheme we proposed is still very robust against decoherence.As shown in Fig.6(b), the final fidelity is beyond 0.85 even when Γ=0.01λ and Γφ=0.001λ.Combined with recent experimental parameters {TΓφ∼100µs,λ>2π×300 MHz,λ/κ>102,λ/Γ>102} and TΓφ=1/Γφ,[67]i.e.,{κ/λ<10−2,Γ/λ<10−2,Γφ/λ<10−5},the GHZ state among three SQs can be generated with a relatively high final fidelity over 97.16%.
5.Conclusion
We have implemented the fast generation of the GHZ state among three SQs by using invariants-based shortcuts. Compared with the STIRAP scheme,the STA scheme we proposed greatly shortens the operation time.The STA scheme needs to neither interpolate the system Hamiltonian nor add auxiliary driving pulses.Besides,the driving pulses are two harmonic pulses which can be obtained very easily in experiment.In addition,the adequate numerical simulations show that the STA scheme is robust against variations in control parameters and decoherence caused by SQs energy relaxations and CPWRs photon leakages.Although the scheme is somewhat sensitive to SQs dephasing,the GHZ state among three SQs can still be achieved with a relatively high final fidelity by adopting recent experimental parameters.
[1]Zhao Z,Chen Y A,Zhang A N,Yang T,Briegel H J and Pan J W 2004 Nature 430 54
[2]Peres A and Terno D 2004 Rev.Mod.Phys.76 93
[3]Hillery M,Buzek V and Berthiaume A 1999 Phys.Rev.A 59 1829
[4]Shor P W 1996 Proceedings of the 37th Symposium on the Foundations of Computer Science(FOCS)(Los Alamitos:IEEE Press)p.56
[5]Knill E 2005 Nature 434 39
[6]Nielsen M A and Chuang I L 2000 Quantum Computation and Quantum Information(Cambridge:Cambridge University Press)
[7]Zeilinger A,Horne M A,Weinfurter H and Zukowski M 1997 Phys. Rev.Lett.78 3031
[8]Zheng S B 2001 Phys.Rev.Lett.87 230404
[9]Leibfried D,Knill E,Seidelin S,Britton J,Blakestad R B,Chiaverini J,Hume D B,Itano W M,Jost J D,Langer C,Ozeri R,Reichle R and Wineland D J 2005 Nature 438 639
[10]Su X L,Tan A H,Jia X J,Zhang J,Xie C D and Peng K C 2007 Phys. Rev.Lett.98 070502
[11]Raimond J M,Brune M and Haroche S 2001 Rev.Mod.Phys.73 565
[12]Su S L,Chen L,Guo Q,Wang H F,Zhu A D and Zhang S 2015 Chin. Phys.B 24 020305
[13]Bishop L S,Tornberg L,Price D,Ginossar E,Nunnenkamp A,Houck A A,Gambetta J M,Koch J,Johansson G,Girvin S M and Schoelkopf R J 2009 New J.Phys.11 073040
[14]Wang Y D,Chesi S,Loss D and Bruder C 2010 Phys.Rev.B 81 104524
[15]Aldana S,Wang Y D and Bruder C 2011 Phys.Rev.B 84 134519
[16]Yang C P 2011 Phys.Rev.A 83 062302
[17]Yang C P,Su Q P and Han S 2012 Phys.Rev.A 86 022329
[18]Makhlin Y,Schön G and Shnirman A 2001 Rev.Mod.Phys.73 357
[19]Yu Y,Han S,Chu X,Chu S I and Wang Z 2002 Science 296 889
[20]Vion D,Aassime A,Cottet A,Joyez P,Pothier H,Urbina C,Esteve D and Devoret M H 2002 Science 296 886
[21]Pashkin Y A,Yamamoto T,Astafiev O,Nakamura Y,Averin D V and Tsai J S 2003 Nature 421 823
[22]Bergmann K,Theuer H and Shore B W 1998 Rev.Mod.Phys.70 1003
[23]Král P,Thanopulos I and Shapiro M 2007 Rev.Mod.Phys.79 53
[24]Zhang C L and Chen M F 2015 Chin.Phys.B 24 070310
[25]Song P J,Lü X Y,Si L G and Yang X X 2011 Chin.Phys.B 20 050308
[26]Hao S Y,Xia Y,Song J and An N B 2013 J.Opt.Soc.Am.B 30 468
[27]Zhang C L and Chen M F 2013 Chin.Phys.B 22 050307
[28]Zhang C L,Li W Z and Chen M F 2014 Opt.Commun.312 269
[29]Wu J L,Song C,Xu J,Yu L,Ji X and Zhang S 2016 Quantum Inf. Process.15 3663
[30]Chen X,Lizuain I,Ruschhaupt A,Guéry-Odelin D and Muga J G 2010 Phys.Rev.Lett.105 123003
[31]Chen X,Torrontegui E and Muga J G 2011 Phys.Rev.A 83 062116
[32]Chen X and Muga J G 2012 Phys.Rev.A 86 033405
[33]del Campo A 2013 Phys.Rev.Lett.111 100502
[34]Torrontegui E,Ibáñez S,Martínez-Garaot S,Modugno M,del Campo A,Guéry-Odelin D,Ruschhaupt A,Chen X and Muga J G 2013 Adv. At.Mol.Opt.Phys.62 117
[35]Martínez-Garaot S,Torrontegui E,Chen X and Muga J G 2014 Phys. Rev.A 89 053408
[36]Ibáñez S,Chen X,Torrontegui E,Muga J G and Ruschhaupt A 2012 Phys.Rev.Lett.109 100403
[37]Ibáñez S,Chen X and Muga J G 2013 Phys.Rev.A 87 043402
[38]Ibáñez S,Li Y C,Chen X and Muga J G 2015 Phys.Rev.A 92 062136
[39]Song X K,Ai Q,Qiu J and Deng F G 2016 Phys.Rev.A 93 052324
[40]Chen Y H,Xia Y,Wu Q C,Huang B H and Song J 2016 Phys.Rev.A 93 052109
[41]Baksic A,Ribeiro H and Clerk A A 2016 Phys.Rev.Lett.116 230503
[42]Kang Y H,Chen Y H,Wu Q C,Huang B H,Xia Y and Song J 2016 Sci.Rep.6 30151
[43]Kang Y H,Huang B H,Lu P M and Xia Y 2017 Laser Phys.Lett.14 025201
[44]Chen Y H,Wu Q C,Huang B H,Song J and Xia Y 2016 Sci.Rep.6 38484
[45]Chen Y H,Xia Y,Chen Q Q and Song J 2014 Phys.Rev.A 89 033856
[46]Chen Y H,Xia Y,Chen Q Q and Song J 2014 Laser Phys.Lett.11 115201
[47]Chen Y H,Xia Y,Chen Q Q and Song J 2015 Phys.Rev.A 91 012325
[48]Wu J L,Ji X and Zhang S 2016 Sci.Rep.6 33669
[49]Wu J L,Ji X and Zhang S 2016 J.Opt.Soc.Am.B 33 2026
[50]Song C,Su S L,Wu J L,Wang D Y,Ji X and Zhang S 2016 Phys.Rev. A 93 062321
[51]Song C,Su S L,Bai C H,Ji X and Zhang S 2016 Quantum Inf.Process. 15 4159
[52]Zhang J,Kyaw T H,Tong D M,Sjöqvist E and Kwek L C 2015 Sci. Rep.5 18414
[53]Liang Y,Wu Q C,Su S L,Ji X and Zhang S 2015 Phys.Rev.A 91 032304
[54]Liang Y,Song C,Ji X and Zhang S 2015 Opt.Express 23 23798
[55]Liang Y,Ji X,Wang H F and Zhang S 2015 Laser Phys.Lett.12 115201
[56]Chen Y H,Xia Y,Song J and Chen Q Q 2015 Sci.Rep.5 15616
[57]Shan W J,Xia Y,Chen Y H and Song J 2016 Quantum Inf.Process.15 2359
[58]Huang B H,Chen Y H,Wu Q C,Song J and Xia Y 2016 Laser Phys. Lett.13 105202
[59]Zhang X,Chen Y H,Wu Q C,Shi Z C,Song J and Xia Y 2017 Laser Phys.27 015202
[60]Ye L X,Lin X,Chen X,He J,Yang R C and Liu H Y 2016 Quantum Inf.Process.15 4159
[61]Huang X B,Chen Y H and Wang Z 2016 Sci.Rep.5 25707
[62]Kang Y H,Chen Y H,Shi Z C,Song J and Xia Y 2016 Phys.Rev.A 94 052311
[63]Kang Y H,Chen Y H,Wu Q C,Huang B H,Song J and Xia Y 2016 Sci.Rep.6 36737
[64]Yu L,Xu J,Wu J L and Ji X 2017 Chin.Phys.B 26 060306
[65]Lewis H R and Riesenfeld W B 1969 J.Math.Phys.10 1458
[66]Kuklinski J R,Gaubatz U,Hioe F T and Bergmann K 1989 Phys.Rev. A 40 6741
[67]Xiang Z L,Ashhab S,You J Q and Nori F 2013 Rev.Mod.Phys.85 623
17 March 2017;revised manuscript
4 May 2017;published online 18 July 2017)
10.1088/1674-1056/26/9/090301
∗Project supported by the National Natural Science Foundation of China(Grant No.11464046).
†Corresponding author.E-mail:jixin@ybu.edu.cn
©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
- Chinese Physics B的其它文章
- Improved control for distributed parameter systems with time-dependent spatial domains utilizing mobile sensor actuator networks∗
- Geometry and thermodynamics of smeared Reissner–Nordström black holes in d-dimensional AdS spacetime
- Stochastic responses of tumor immune system with periodic treatment∗
- Cancelable remote quantum fingerprint templates protection scheme∗
- A high-fidelity memory scheme for quantum data buses∗
- Determination of the thermal noise limit in test of weak equivalence principle with a rotating torsion pendulum∗

