具有非局部边界的退化抛物方程组的爆破解
杨 婕,刘丙辰,张长城
(中国石油大学(华东)理学院,山东青岛 266580)
具有非局部边界的退化抛物方程组的爆破解
杨 婕,刘丙辰,张长城
(中国石油大学(华东)理学院,山东青岛 266580)
本文研究了具有非局部边界条件和非局部源的退化抛物方程组的弱解问题.利用基于比较原理的上下解的方法,在权函数和初始条件的假设下,获得了该方程组问题的爆破临界指标.此外,还获得了同时爆破解趋于爆破时间时的渐近行为,推广了已有的结果.
退化抛物方程组;临界指标;渐近行为;非局部边界
1 引言
在这篇文章中,考虑如下具有非局部源的退化抛物方程组问题
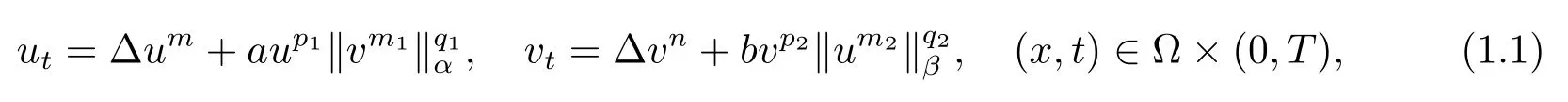
其边界条件为
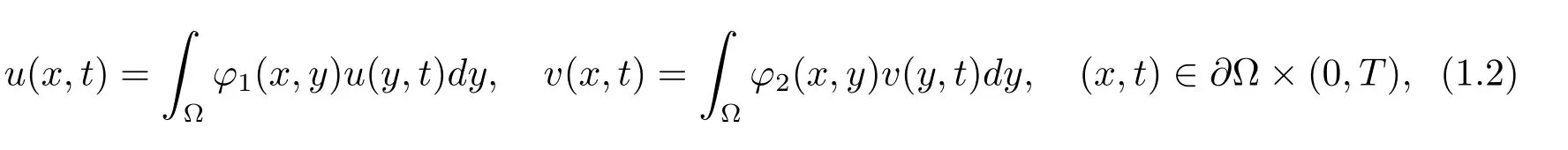
其初值在边界上满足相容性条件
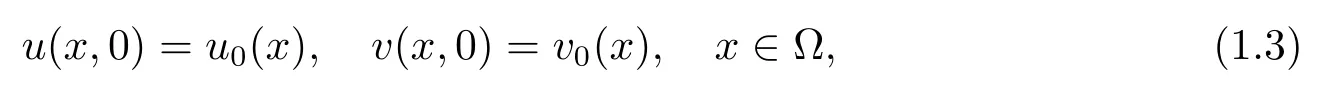
其中Ω 是有光滑边界的有界区域;‖·‖α和‖·‖β是Lα(Ω)和Lβ(Ω)范数;m,n,α,β>1;p1,p2≥0;a,b,q1,q2,m1,m2>0;权函数ϕ1(x,y)和ϕ2(x,y)是上的非负函数,并且满足初值u0,v0∈C2+ν,常数ν∈(0,1).
对于多孔介质方程解的爆破现象,在过去的十几年中得到了很大的关注(参见文献[1–14]).多孔介质方程和系统已经成为非常重要的偏微分方程研究领域,具有深刻的物理背景,例如在多孔介质力学、流体力学、气体流量、种群生态领域中,更多的细节参见文献[15–22].
Galaktionov,Kurdyumov和Samarskii在文献[23,24]中研究了
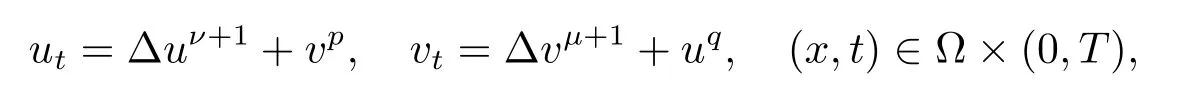
其具有齐次狄利克雷边界条件,结果如下:如果1≤p<1+µ,1≤q<1+ν,则在初值和边界条件下,解整体存在.如果p=1+µ,q=1+ν,且在狄利克雷边界条件下的最小的特征值满足λ1<1,则对任意初值u0,v0≥0,u0+v0不恒等于0,有T0<+∞.如果p>1+µ且q>1+ν,则存在初值u0,v0≥0使上式成立.假设p,q≥1,令m=pq−(1+µ)(1+ν).
(i)若m<0或m=0,且|Ω|充分小,则对任意u0,v0,解整体存在.
(ii)若m>0,则存在初值的集合使解整体存在.
杜力力在文献[9]中得到了如下系统的爆破解
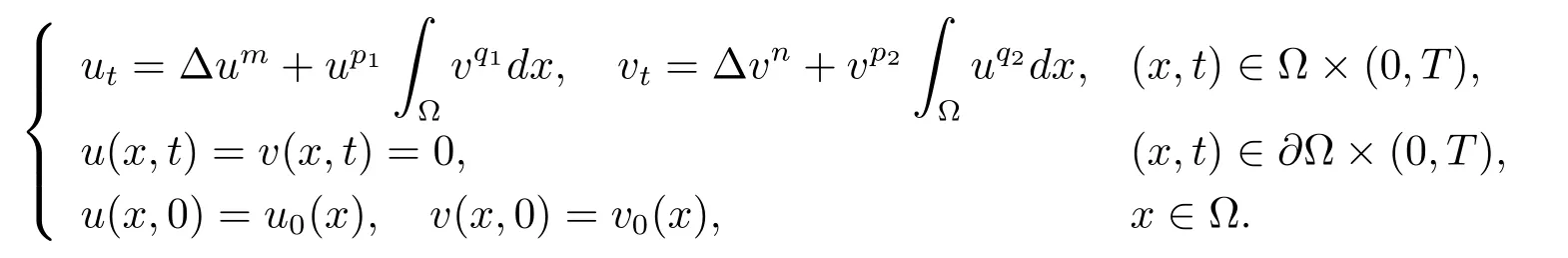
他们对于以上的系统建立了爆破临界指标,如果m>p1,n>p2,q1q2<(m−p1)(n−p2),那么任意非负解整体存在.如果m<p1或n<p2或q1q2>(m−p1)(n−p2),那么任意非负解对于充分大的初值在有限时刻爆破,对于充分小的初值整体存在.如果m>p1,n>p2,q1q2=(m−p1)(n−p2),那么任意非负解对于充分小的定义域|Ω|整体存在.假设p1=0或p1>m;p2=0或p2>n;q1>n,q2>m且满足q2>p1−1,q1>p2−1以及对初值的一些假设条件
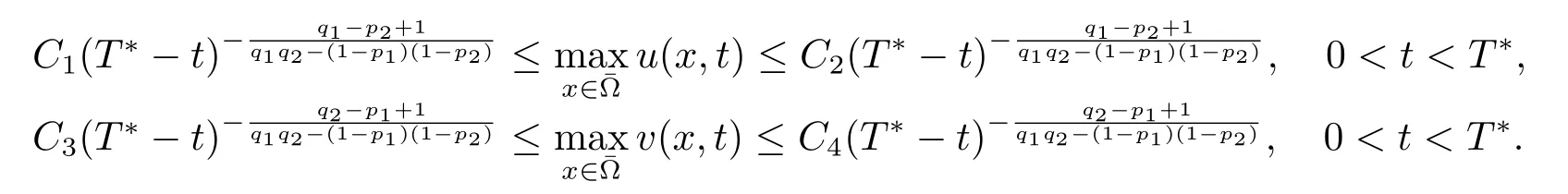
叶专和许孝精在文献[25]中考虑如下具有非局部边界条件和非局部源的多孔介质系统
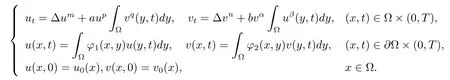
主要结果如下:对于任意的δ>0满足并且假设m>p,n>q,(m−p)(n−α)>qβ,那么任意一个非负的解(u,v)都是整体存在的.如果并且以下条件之一成立:
(i)m<p;
(ii)n<α;
(iii)(m−p)(n−α)<qβ,
那么任意非负解(u,v)对于充分小的初值整体存在.如果m<p或n<α或(m−p)(n−α)<qβ,那么任意非负解(u,v)对于充分大的初值在有限时刻爆破.对于任意的δ>0满足并且假设m>p,n>q,(m−p)(n−α)=qβ,那么任意非负解(u,v)对于充分小的a和b整体存在.在假设m=n=1,qβ>(1−α)(1−p)以及对于初值的一些假设下,他们给出解的爆破profile.在文献[25]中没有考虑m>p,n>q,(m−p)(n−α)=qβ情况下的爆破现象.在本文中,可以通过对系统(1.1)–(1.3)的研究,得到该情况的相关结果(参见下面的定理3.1(iii)的证明).
在下节中,将建立弱解的局部存在定理,并给出一些辅助性引理.在第3节中,将分别讨论十个指标,两个权函数和两个系数对整体存在和爆破解的影响.在最后一节中,解的渐近性质将在适当的假设条件下给出.
2 局部存在性和比较原理
对于0<T<+∞,令ΩT=Ω×(0,T),ST=∂Ω×(0,T).众所周知的,退化方程不一定具有古典解,下面给出问题(1.1)–(1.3)的弱解的定义.
定义 2.1在上对于所有的T>0成立的向量函数(u(x,t),v(x,t))被称作系统(1.1)–(1.3)的上解(或下解),如果以下条件成立:
(i)u(x,t),v(x,t)∈L∞(QT);
(ii)u(x,t),v(x,t)≤(≥)0,(x,t)∈ST;u(x,0)≤(≥)u0(x),v(x,0)≤(≥)v0(x),a.e.x∈Ω;
(iii)对于任意的t∈[0,T]和
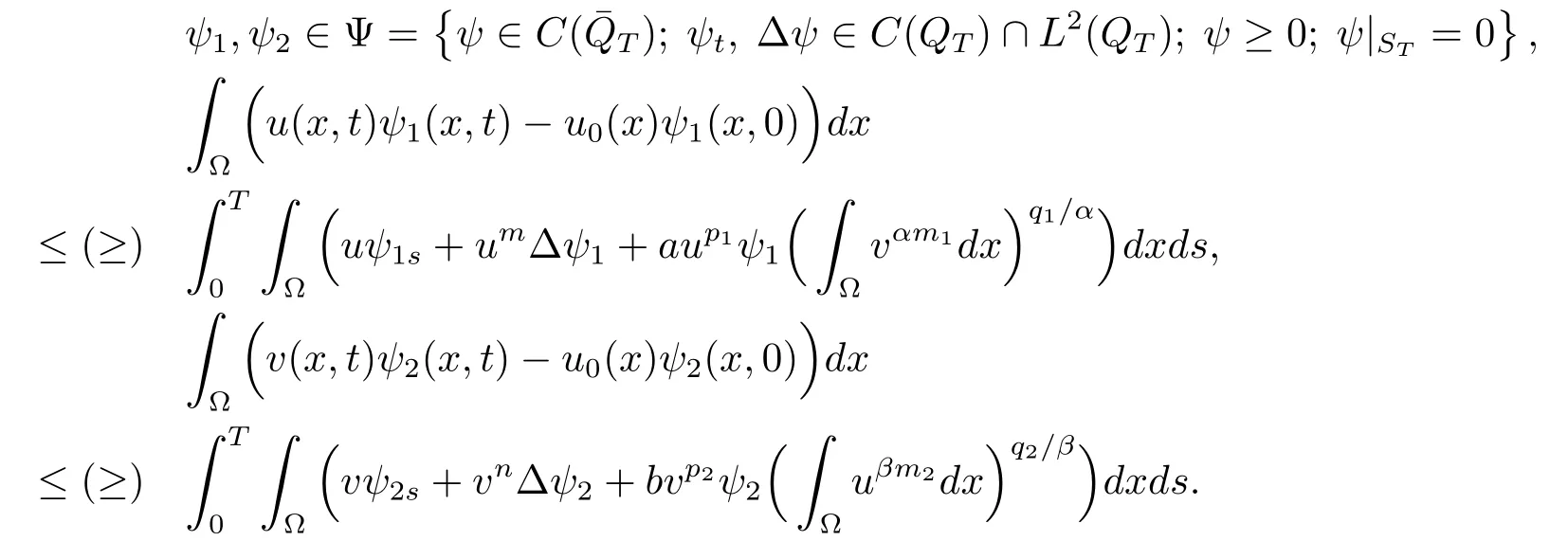
系统(1.1)–(1.3)的一个弱解是一个向量函数,同时也是系统(1.1)–(1.3)的一个上解和下解.对任意的T<∞,如果(u,v)是系统(1.1)–(1.3)的解,就说(u,v)是整体存在的.接下来,构建整体存在定理,因为它的证明是标准的,在这里仅给出结果.
定理2.1给定u0,v0∈L∞(Ω),则对某些T∗=T∗(u0,v0)>0,存在系统(1.1)–(1.3)的非负弱解(u(x,t),v(x,t))对于每一个T<T∗成立,则有T∗=∞或者解发生爆破.
引理2.1(比较原理)令和分别是系统(1.1)–(1.3)的非负下解和非负上解.如果有则在ΩT上,成立.
3 爆破临界指标
定理3.1系统(1.1)–(1.3)的非负解具有以下的结果.
(i)如果m>p1,n>p2,(m−p1)(n−p2)>m1q1m2q2,那么所有的非负解都整体存在.
(ii)令m<p1或者n<p2或者(m−p1)(n−p2)<m1m2q1q2,对于大初值,解在有限时刻爆破;对于小初值,且和解整体存在.
(iii)令m>p1,n>p2,(m−p1)(n−p2)=m1q1m2q2,若存在小区域Ω或者存在小的a和b,则解整体存在;若存在大初值和充分大的球形域Ω,或者存在大的a和b,则解在有限时刻爆破.
证定理3.1(i).首先,定义如下的边值问题
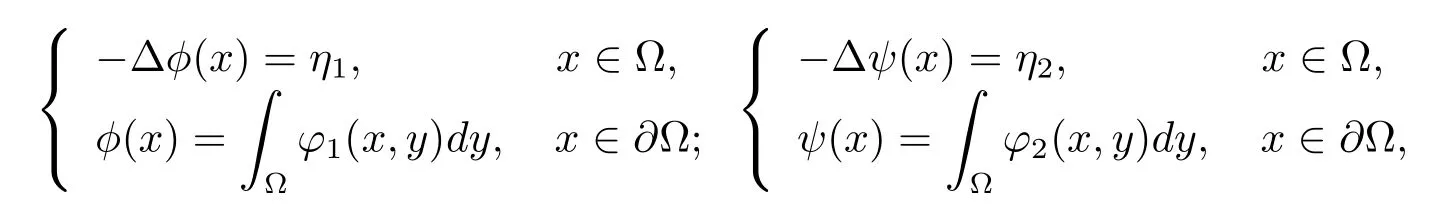
其中η1,η2都是正常数并满足0<φ(x)≤1,0<ψ(x)≤1.做如下定义
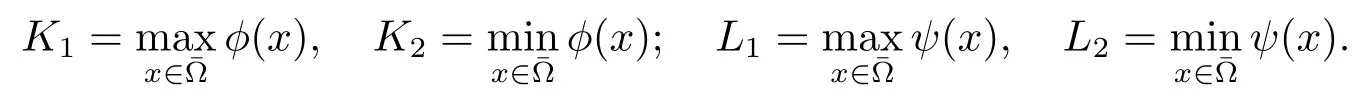
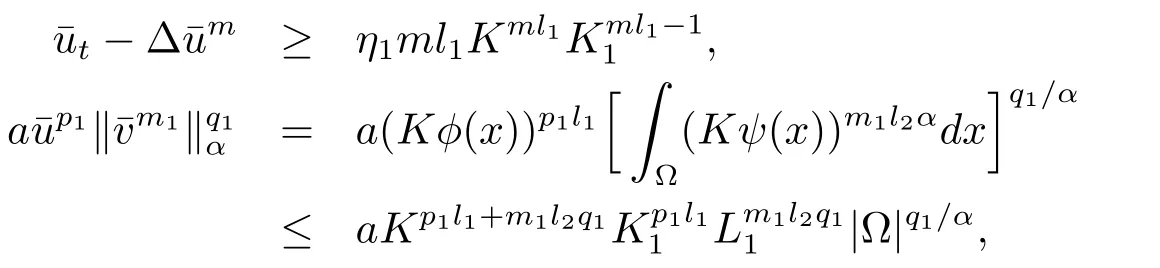
其中在第一个不等式中利用了ml1<1.类似的,可以得到
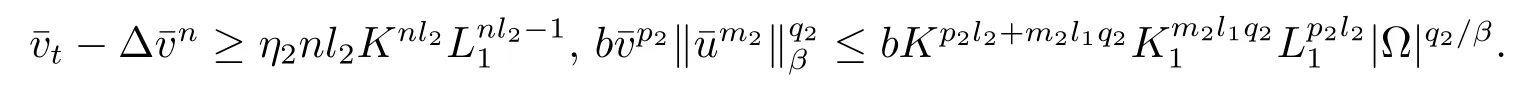
定义
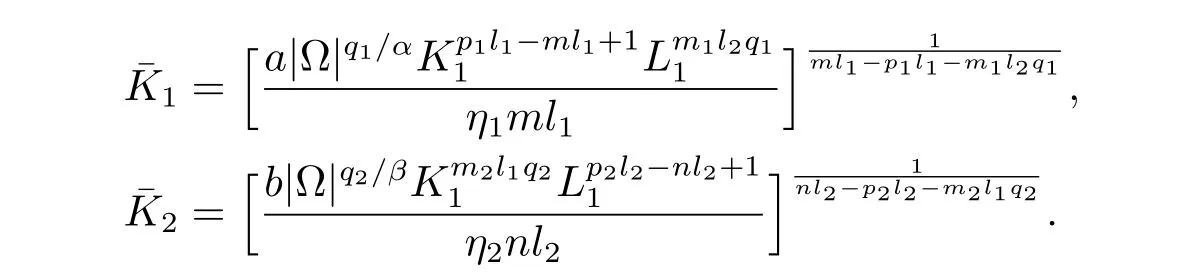
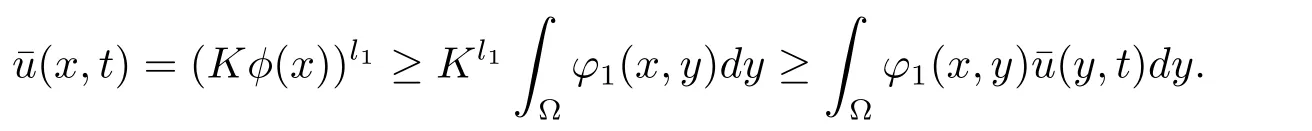
证定理3.1(ii).考虑下面的系统
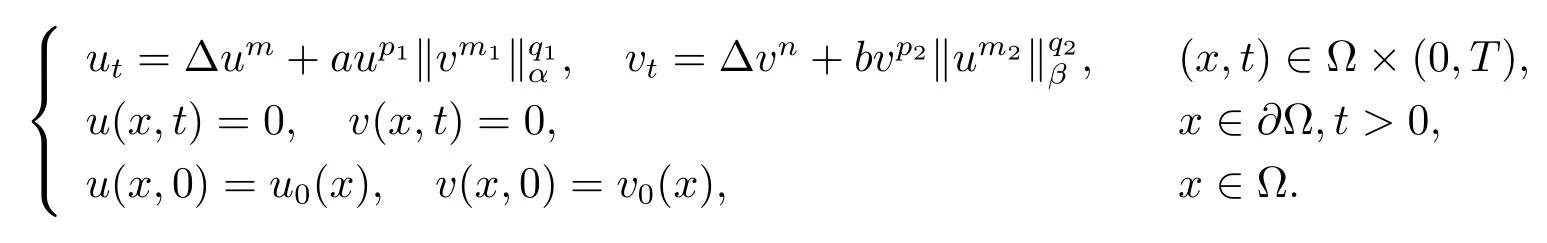
将在一个有上界的区域Ω中构造一个上解,在此区域中u,v>0.利用参考文献[12]中的方法并将它应用到退化方程中去.只需考虑下面的问题

其中w+=max{0,w}.令ψ(x)是一个非平凡非负的连续函数并且在边界∂Ω上为零.不失一般性,假设0∈Ω,并且ψ(0)>0.将构造一个爆破的上解来完成证明.令
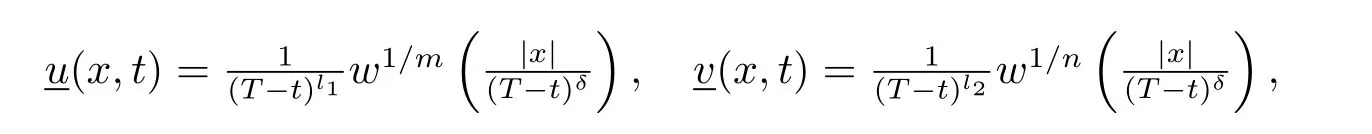
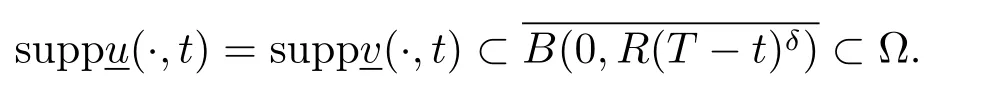
经过直接的计算得
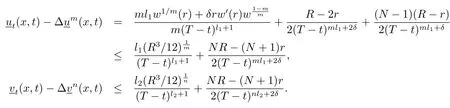
注意到T<1充分小.
情形(1)如果0≤r≤NR/(N+1),有w(r)≥R3(3N+1)/(12(N+1)3),那么
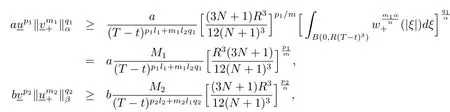
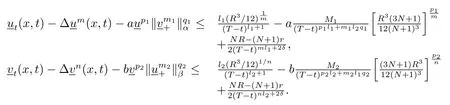
情形(2)如果NR/(N+1)<r≤R,那么
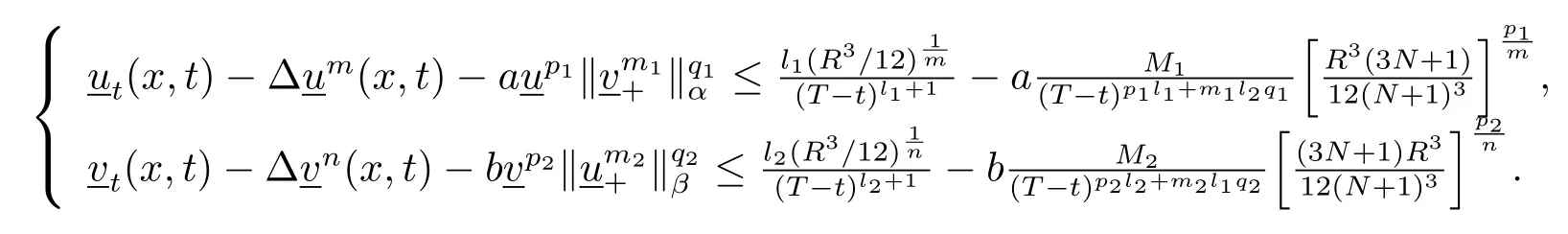
参照参考文献[15]中的引理2.2,存在两个正常数l1,l2满足
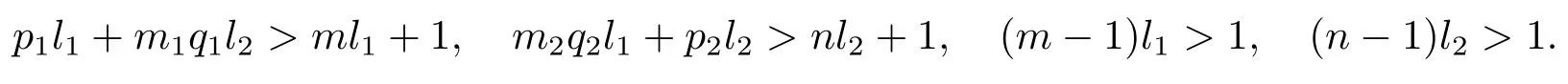
选择一个充分小的正常数δ使得
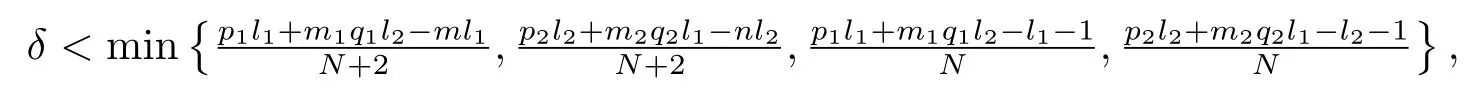
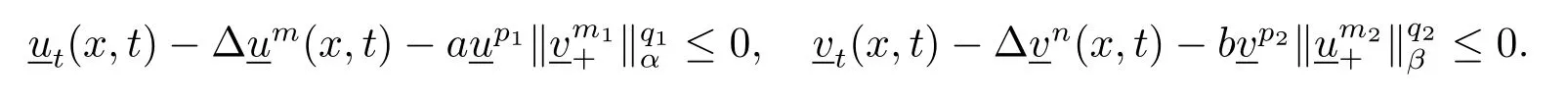
由于ϕ(0)>0并且ϕ(x)连续,存在两个正常数ρ和∈使得ϕ(x)≥∈对所有的x∈B(0,ρ)⊂Ω成立.选择T足够小来保证B(0,RTδ)⊂B(0,ρ),因此在ST上成立.对于足够大的有成立.根据比较原理,如果有得到即(u,v)在有限时刻爆破.根据比较原理,由于系统(1.1)–(1.3)的任意非负解(u,v)一定在有限的时刻爆破.
第一步证明m<p1的情况.首先,利用参考文献[26]中提供的方法,并且令
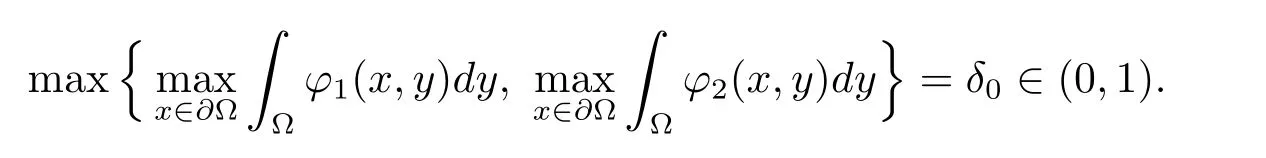
令w(x)是下面椭圆边值问题的解:−Δw(x)=1,x∈Ω;w(x)=C0,x∈∂Ω.存在正常数M>0与C0无关且使得C0≤w(x)≤C0+M成立,取C0充分大使得令,其中K1,K2将在后边被定义.经计算
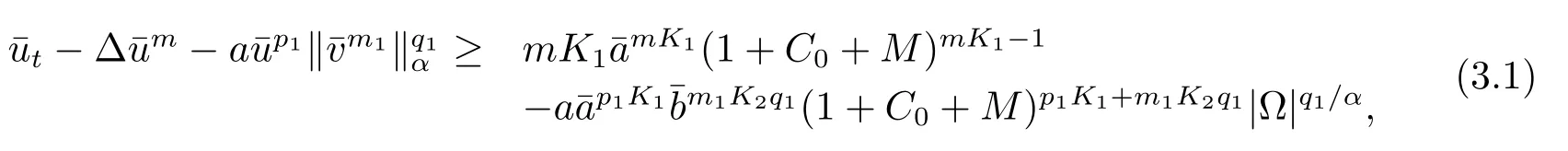
选择0<K1<1满足mK1≤1.类似的,可以得到
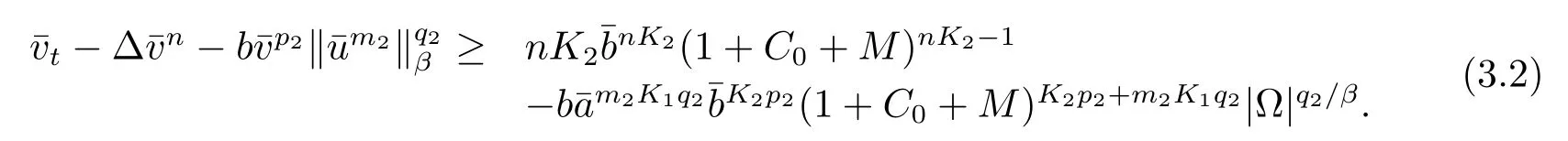
由于m<p1,对于固定的如果充分小,可以得到不等式下面来计算边界条件:由K1,δ0∈(0,1),可得并且类似的,得到利用比较原理,得到则(u,v)整体存在.
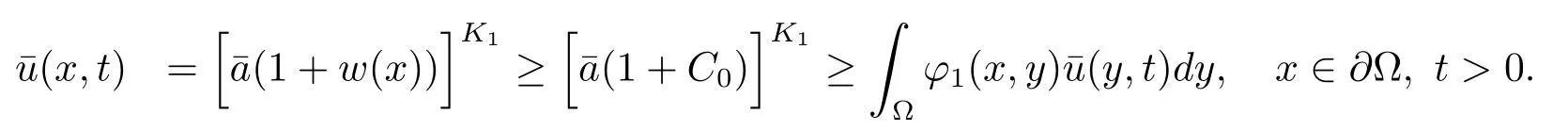
第二步n<p2情况下的证明可由第一步直接平推而来,不再赘述.
第三步对于(m−p1)(n−p2)<m1m2q1q2的情况,分为以下三部分进行讨论.
a)如果m=p1,返回到(3.1)和(3.2)式,选取充分小的并且与不相关,利用第一步的论点与论据得到结论.
b)如果n=p2,情况与上面类似,证明省略.
c)如果m>p1,n>p2,可以得到下面的不等式
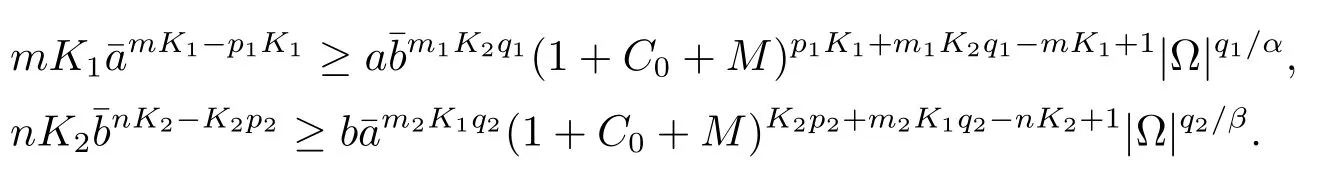
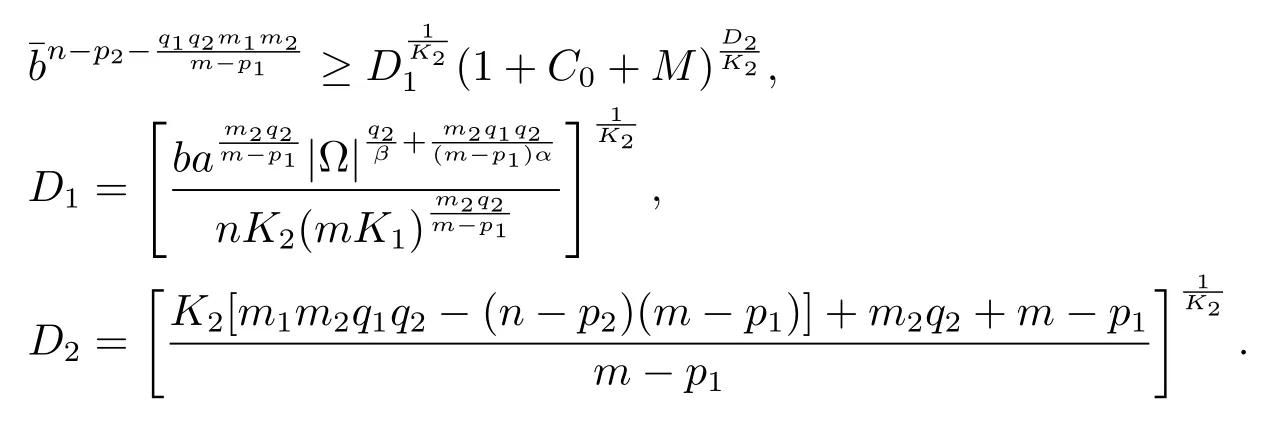
证定理3.1(iii).如果m>p1,n>p2,(m−p1)(n−p2)=m1q1m2q2,那么存在两个正数l1,l2<1满足定义,其中的K将在后面被定义.用跟定理3.1(i)中相同的创建估计的方式,可得
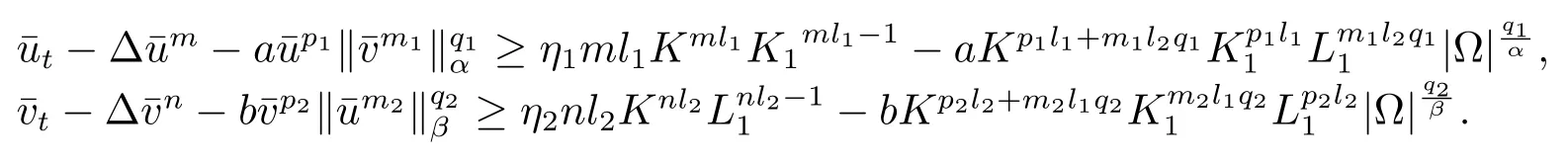
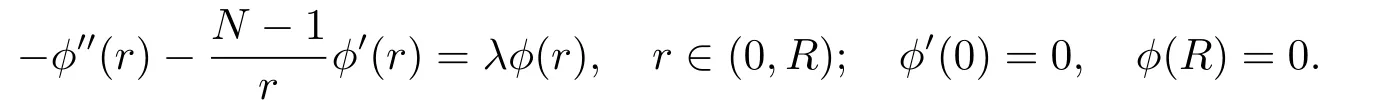
易见,φR(r)可以在B中标准化得到φR(r)>0,并且有由特征值和特征方程的性质(令),知道和成立,其中和φ1是单位球B1(0)内的第一个特征值和相应的标准化特征函数.此外,定义函数为如下形式下面,将会证明在球B=B(0,R)中在有限的时间内爆破.因此在更大的区域Ω中爆破.经过直接的计算,
4 渐近性质
这一部分,讨论系统(1.1)–(1.3)在适当假设条件下的渐近性质.假设m=n=1,p1<1,p2<1,m1q1m2q2>(1−p2)(1−p1),并且有成立.当m=n=1时,系统(1.1)–(1.3)变为
假设系统的解(u,v)在有限时间T时爆破.为了方便起见,定义
首先证明在假设条件下解在有限时间内爆破.如果p1<1,p2<1,m1q1m2q2>(1−p2)(1−p1),那么存在两个正常数α2,β2>1使得
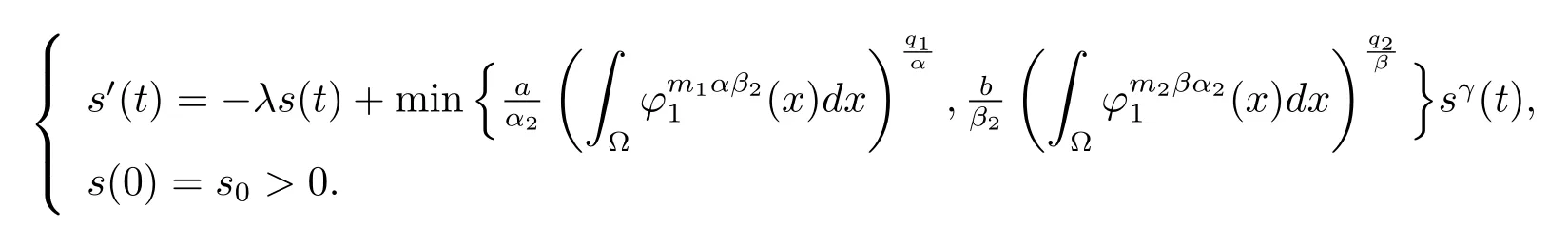
如果s0足够大的话,s(t)在有限时间T(s0)爆破.令其中λ是如下特征问题的第一特征值0,x∈∂Ω,并且ϕ1(x)是相应的特征方程,有经过计算
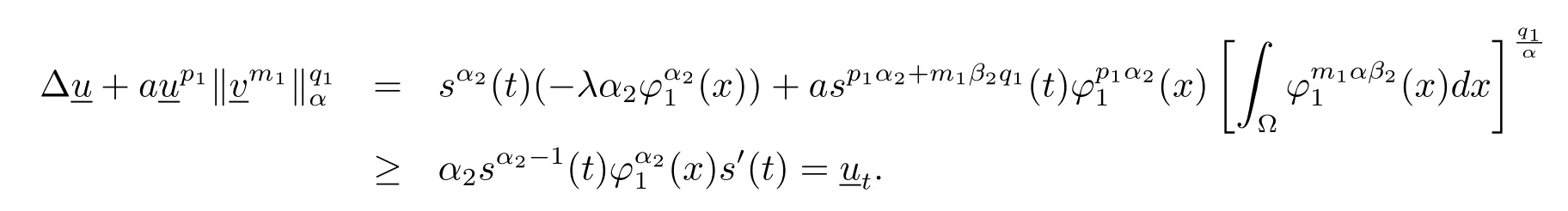
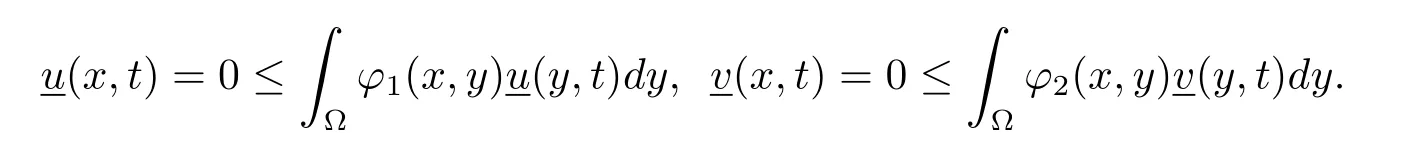
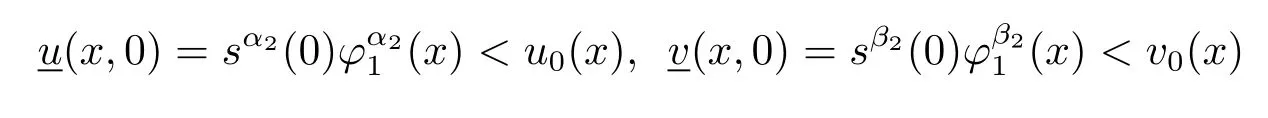
得到,所以(u,v)在有限时间内爆破.参照参考文献[25],得到下面的引理.
引理4.1假设系统(4.1)的解在T时爆破,则
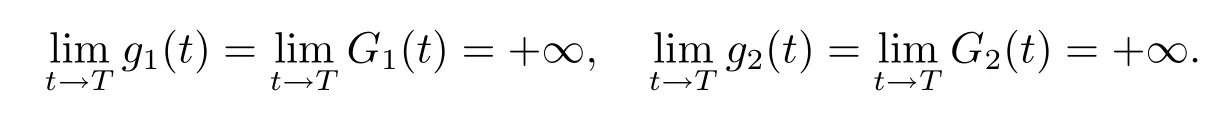
引理4.2在引理4.1的条件下,下面的极限成立
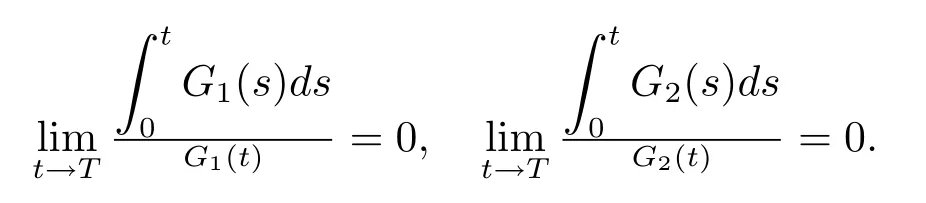
引理4.3假设对任意的x∈¯Ω有Δu0,Δv0≤0,对(x,y)∈∂Ω×Ω,有ϕ1(x,y)≥0,ϕ2(x,y)≥0,并且 Z
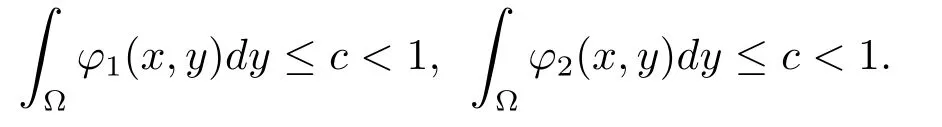
那么Δu≤0,Δv≤0在区域Ω中有一个任意的紧支集.
证易见该引理是参考文献[1]中引理5.1经过小的修改后的直接结果.
引理4.4在引理4.1–4.3的条件下,对区域Ω中的任意紧支集,有
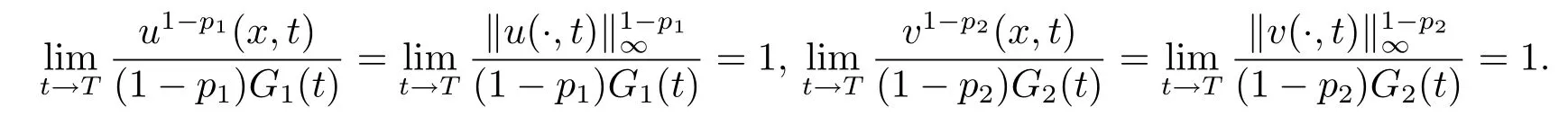
证证明与参考文献[25]类似.
定义4.1如果接下来定义f(t)~g(t).显而易见的,等价关系具有以下的性质:
1)如果f(t)~g(t),∀k∈R,有fk(t)~gk(t);
2)如果f(t)~g(t),g(t)~h(t),有f(t)~h(t);
3)如果f(t)~g(t),ϕ(t)~ ψ(t);有f(t)ϕ(t)~g(t)ψ(t).
4)如果f(t)~g(t),有
定理4.1在引理4.4以及m1q1m2q2>(1−p1)(1−p2)的条件下,有
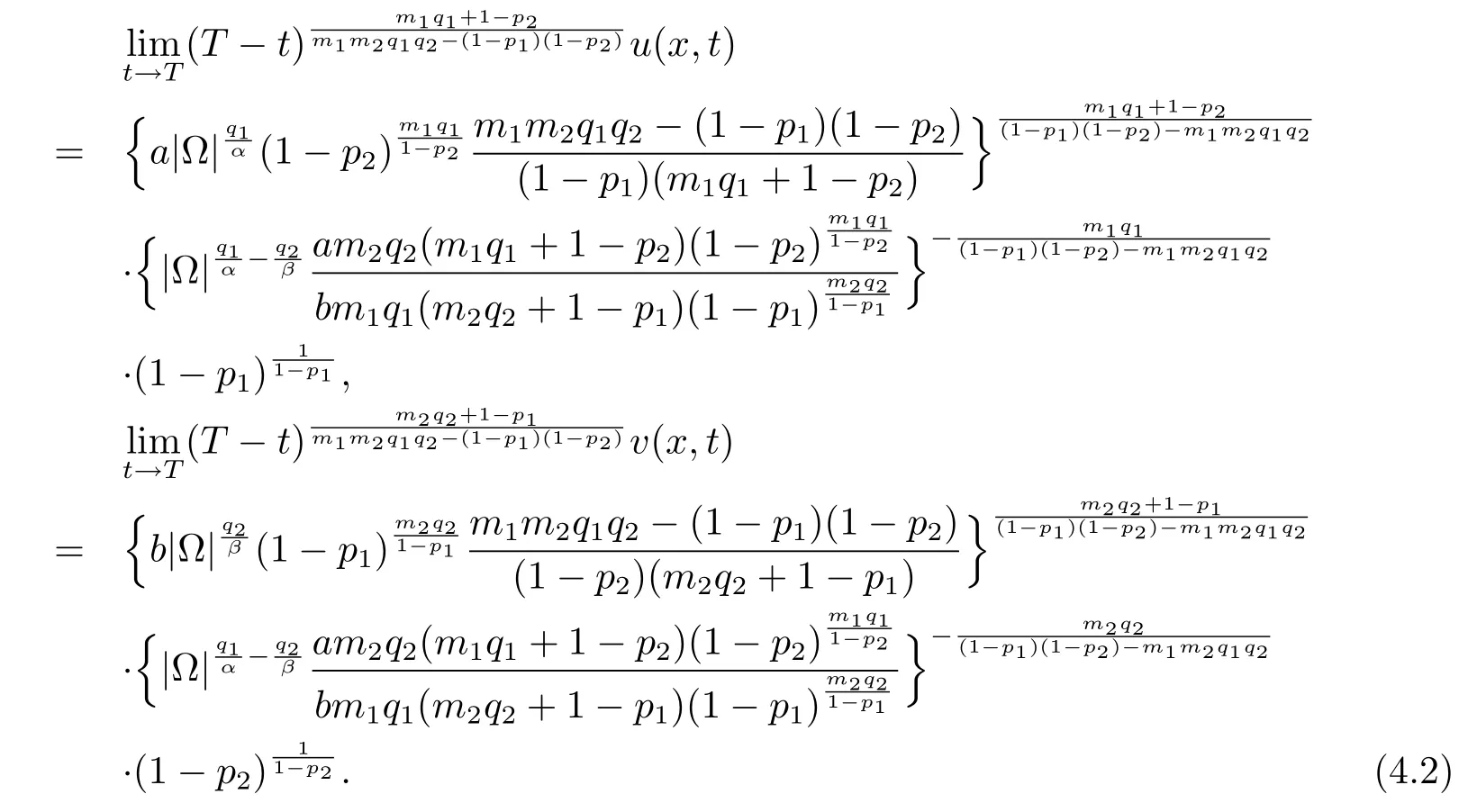
证由于
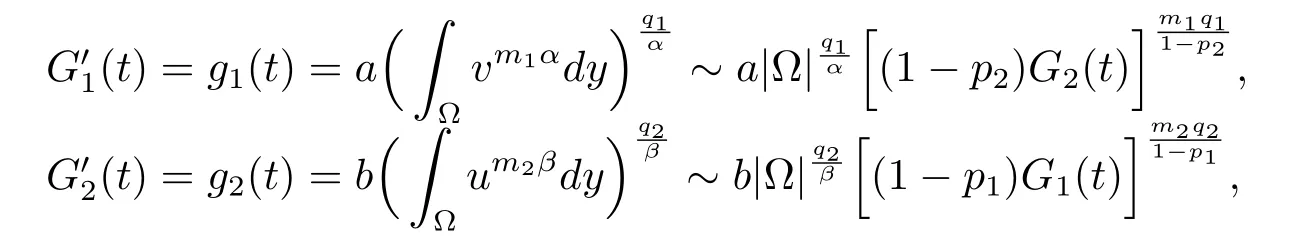
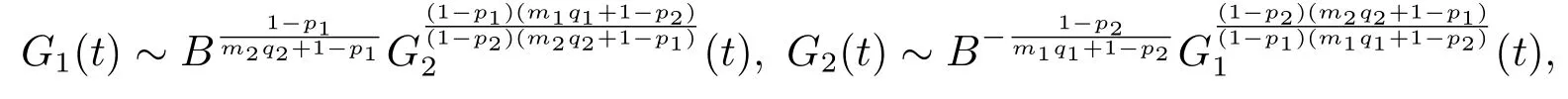
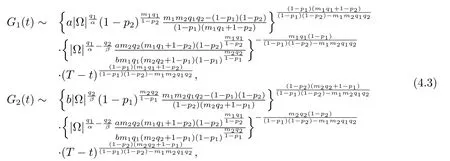
由引理4.4的结论,即
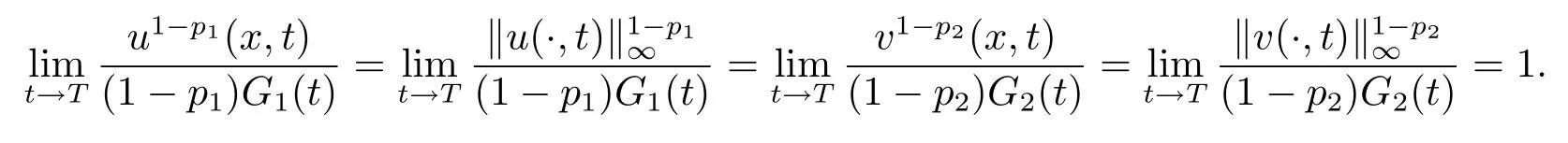
将上面的等式与(4.3)结合起来,就得到了期望的结果.
[1]Cui Zhoujin,Yang Zuodong.Roles of weight functions to a nonlinear porous medium equation with nonlocal source and nonlocal boundary condition[J].J.Math.Anal.Appl.,2008,342(1):559–570.
[2]Lin zhigui,Liu Yurong.Uniform blow-up profile for diffusion equations with nonlocal source and nonlocal boundary[J].Acta Math.Sci.,2004,24B(3):443–450.
[3]Du Lili.Blow-up for a degenerate reaction-diffusion system with nonlinear localized sources[J].J.Math.Anal.Appl.,2006,324(1):304–320.
[4]Wang Minxing,Wei Yunfeng.Blow-up properties for a degenerate parabolic system with nonlinear localized sources[J].J.Math.Anal.Appl.,2008,343(2):621–635.
[5]Fan Mingshu,Du Lili,He Qiaolin.Blow-up properties for a degenerate parabolic system with nonlinear localized sources[J].J.Comput.Appl.Math.,2010,235(1):91–101.
[6]Lu Haihua,Wang Mingxin.Global solutions and blow-up problems for a nonlinear degenerate parabolic system coupled via nonlocal sources[J].J.Math.Anal.Appl.,2007,333(2):984–1007.
[7]Du Lili,Mu Chunlai.Global existence and blow-up analysis to a degenerate reaction-diffusion system with nonlinear memory[J].Nonl.Anal.,2008,9(2):303–315.
[8]Deng Wenbo.Global existence and finite time blow-up for a degenerate reaction-diffusion system[J].Nonl.Anal.,2005,60(5):977–991.
[9]Du Lili.Blow-up for a degenerate reaction-diffusion system with nonlinear nonlocal sources[J].J.Comput.Appl.Math.,2007,202(2):237–247.
[10]Deng Wenbo,Li Yangxing,Xie Chunhua.Existence and nonexistence of global solutions of some nonlocal degenerate parabolic equations[J].Appl.Math.Lett.,2003,16(5):803–808.
[11]Fila M,Quittner P.The blow-up rate for a semilinear parabolic system[J].J.Math.Anal.Appl.,1999,238(2):468–476.
[12]Souplet Ph.Uniform blow-up profiles and boundary behavior for diffusion equations with nonlocal nonlinear source[J].J.Di ff.Equa.,1999,153(2):374–406.
[13]Wang Mingxi.Blow-up rate estimates for semilinear parabolic systems[J].J.Di ff.Equa.,2001,170(2):317–324.
[14]Lin Zhigui,Xie Chunhua.The blow-up rate for a system of heat equations with nonlinear boundary conditions[J].Nonl.Anal.,1998,34(5):767–778.
[15]Day WA.Extensions of property of heat equation to linear thermoelasticity and other theories[J].Quart.Appl.Math.,1982,40(3):319–330.
[16]Day WA.A decreasing property of solutions of parabolic equations with applications to thermoelasticity[J].Quart.Appl.Math.,1982/83,40(1):468–475.
[17]Diaz J I,Kersner R.On a nonlinear degenerate parabolic equation in in filtration or evaporation through a porous medium[J].J.Di ff.Equa.,1987,69(3):368–403.
[18]Cantrell R S,Cosner C.Di ff usive logistic equations with inde finite weights:population models in disrupted environments II[J].SIAM J.Math.Anal.,1991,22(4):1043–1064.
[19]Furter J,Grinfeld M.Local vs.nonlocal interactions in population dynamics[J].J.Math.Biol.,1989,27(1):65–80.
[20]Carlson D E.Linear thermoelasticity,encyclopedia of physics,Vol.2[M].Berlin:Springer,1972.
[21]陈佳佳,穆春来.一类非线性抛物方程组解的爆破时间上下界估计[J].数学杂志,2012,32(5):897–903.
[22]Li Mei,Xie Chunhong.Global existence and blow-up of solutions for degenerate paraboloc systems[J].J.Math.,2004,24(2):197–203.
[23]Galaktionov V A,Kurdyumov S P,Samarskii A A.A parabolic system of quasi-linear equations I[J].Di ff.Equa.,1983,19(3):1558–1571.
[24]Galaktionov V A,Kurdyumov S P,Samarskii A A.A parabolic system of quasi-linear equations II[J].Di ff.Equa.,1985,21(1):1049–1062.
[25]Ye Zhuan,Xu Xiaojing.Global existence and blow-up for a porous medium system with nonlocal boundary conditions and nonlocal sources[J].Nonl.Anal.,2013,82(1):115–126.
BLOW-UP SOLUTIONS TO DEGENERATE PARABOLIC EQUATIONS WITH NONLOCAL BOUNDARY
Yang Jie,Liu Bing-chen,Zhang Chang-cheng
(School of Science,China University of Petroleum,Qingdao 266580,China)
In this paper,we consider the weak solutions of the degenerate parabolic equations coupled via nonlocal sources,subject to nonlocal boundary conditions.By using the comparison principle,the critical blow-up exponent is obtained under the help of the weighted functions and the initial data.Moreover,asymptotic behavior near blow-up time is obtained for simultaneous blow-up solutions,which extends the known results in the previous paper.
degenerate parabolic equations;critical exponents;asymptotic behavior;nonlocal boundary
35K65;35K61;35B33;35B40
O175.29
A
0255-7797(2017)06-1275-12
2016-02-12接收日期:2016-04-22
国家自然科学基金(11201483);山东省自然科学基金(ZR2016AM12);中央高校基本科研业务费专项资金(15CX08011A).
杨婕(1991–),女,山东潍坊,硕士,主要研究方向:非线性偏微分方程.

