人工带隙材料的拓扑性质∗

孙晓晨何程卢明辉 陈延峰

1)(南京大学,固体微结构国家实验室,材料科学与工程系,南京 210093)2)(人工微结构科学与技术协同创新中心,南京 210093)

人工带隙材料的拓扑性质∗

孙晓晨1)何程1)2)卢明辉1)2)†陈延峰1)2)

1)(南京大学,固体微结构国家实验室,材料科学与工程系,南京 210093)2)(人工微结构科学与技术协同创新中心,南京 210093)

(2017年9月20日收到;2017年11月6日收到修改稿)

近年来,人工带隙材料(如声子晶体和光子晶体)由于其优异的性能,已成为新一代智能材料的研究焦点.另一方面,材料拓扑学由凝聚态物理领域逐渐延伸到其他粒子或准粒子系统,而研究人工带隙材料的拓扑性质更是受到人们的广泛关注,其特有的鲁棒边界态,具有缺陷免疫、背散射抑制和自旋轨道锁定的传输等特性,潜在应用前景巨大.本文简要介绍拓扑材料特有的鲁棒边界态的物理图像及其物理意义,并列举诸如光/声量子霍尔效应、量子自旋霍尔效应、Floquet拓扑绝缘体等相关工作;利用Dirac方程,从原理上分析光/声拓扑性质的由来;最后对相关领域的发展方向和应用前景进行了相应的讨论.

人工带隙材料,拓扑,Dirac方程

1 引 言

剑仙手中掐诀,提起御剑之气,足下宝剑载其飘行于湖面之上.湖畔一片竹林,眼见剑锋一股真气溢出,排开竹海,竟从林间撕开一条去路.竹林外,一块大石挡住去路.那剑气仿佛有灵气一般,邻近大石一个急转,贴着石壁绕了过去.

浩浩乎如凭虚御风而不知其所止,飘飘乎如遗世独立羽化而登仙.受“摩尔时代即将终结”这一世纪难题所困惑的科学家们希望在导电材料中做出犹如仙侠小说中描述般的御剑之术.它们一往无前不受外界干扰,能够穿越杂质,绕行障碍物.这样一来,电流在电子器件的沟壑中穿行时,其传输效率将大大提高,热量消耗大大减小.这不仅可以提高器件性能,更可以极大地降低器件材料的需求加工难度,甚至可以实现更丰富的性能,让人们可以在器件功能上发挥更丰富的想象力.科学家经过多年研究发现,如果物理学中真的有御剑之术,那么保护电子不受外物干扰的御剑之气,就是拓扑.受到拓扑保护的材料,其内部电流不受杂质、无序结构影响,可以实现快速、高效、低能耗的信号传输.

图1 御剑术(来自百度图片,出自游戏《天下》)Fig.1.Control the sword(From Baidu Picture,Game“TIANXIA”)

拓扑是一个数学概念.通俗来讲,对物体进行连续形变,而不“剪开”或者“黏连”,物体的某些性能指标将会保持不变,而变换前后的物体“拓扑等价”.举个具体的例子,一个球拓扑等价于一个碗;一个面包圈拓扑等价于一个水杯.但是,球和面包圈拓扑不等价.也就是说,球和面包圈具有不同的拓扑数,如图2所示.在凝聚态物理领域,随着晶体能带理论的发展,人们发现以矢量k为底流形的倒空间结构(动量-能量关系,即能带),也同样可以视为类似球体或者面包圈的流形,从而具有不同的拓扑数.如果系统的某种性质——例如电子输运性能——只和这个拓扑数有关,那么除非这个系统变化大到颠覆了拓扑数,否则电子输运性能总会保持不变,例如手征性、无损耗、电流方向等.遵循着这一思路,1984年Berry把几何相位的概念正式引入到物理领域,在前人工作的基础上[1],提出了“Berry phase”的概念[2,3].这个概念迅速引领了拓扑相,以及拓扑相变的蓬勃发展[4].其中最典型的例子就是QH家族.

图2 不同的拓扑类[5]Fig.2.Di ff erent topology classes[5].

1879年,美国物理学家Hall在研究金属导电机理时发现了霍尔效应:电流垂直于外加磁场(B)通过导体时,载流子发生偏转,垂直于电流和磁场的方向出现电势差.如果用霍尔电阻(RH)表示这种互相垂直的电势差和输入电流之比,会发现其数值随B线性增加[6],如图3(a)所示.1980年,德国物理学家von Klitzing发现了整数量子霍耳效应[7]:在低温强磁场下,二维电子气被限制在一层极薄的层状材料之内运动.此时的霍尔电阻与垂直磁场B的关系在总体上升趋势中会出现数值为RH=h/(ne2)(n为整数)的平台.在平台处,霍尔电阻对载流子浓度、迁移率大小等均不敏感,即具有某种量子化的特性.1982年,Thouless等指出:这种量子化特性的根源来自系统能带整体具有的拓扑不变量n,并且引入陈数(Chern number,即陈省身数)来描述这个拓扑不变量.进一步,这种体能带拓扑性质对量子化霍尔电导的影响被总结成为Thouless-Kohmoto-Nightingale-Nijs(TKNN)关系[8].具有量子霍尔效应的拓扑非平庸系统陈数非零,而真空或普通绝缘体等平庸系统陈数为零.他们还指出,这种存在于能带中的阶梯状“鲁棒”特性可以直接对应于边界态传输时的“拓扑保护”现象:材料表面电子将会单向传输,且完全“背散射抑制”——电流不会被材料表面的杂质、缺陷散射掉——这就是凝聚态物理中的“御剑之气”.从此,拓扑物态的研究成为凝聚态物理研究中的重要方向,拓扑材料研究也蓬勃发展.历代科学家为拓扑现象扩展实验平台、降低实验难度前赴后继地努力着.1988年,Haldane[9]提出了一种在周期性磁通中实现整数量子霍尔效应的方法,在理论上克服了拓扑性质依赖于外界强磁场的瓶颈.尽管总磁通为零,电子依然会形成非零的边界电导[10].值得一提的是,Thouless和Haldane凭借在拓扑相物质和拓扑相变方面的贡献,与Kosterlitz一起三人分享了2016年获的诺贝尔物理学奖.2005年和2006年,Kane和Zhang等分别提出,利用电子自旋轨道耦合,可以在零磁场下得到一对共轭的自旋相反的无能隙边界态.这对自旋边界态可以视为一对量子反常霍尔效应的结合,它们在体能带能隙中简并,并受到时间反演对称性保护.这就是量子自旋霍尔效应(二维)[11].这一现象于2007年在HgTe量子阱实验体系中得以实现[12].类似量子霍尔效应,这种系统可以用另外一类拓扑不变量来描述:Z2拓扑不变量[13]或自旋陈数(spin Chern number)[14].在最近十年的发展中,凝聚态拓扑学逐渐由二维系统扩展到三维系统.2009年,遵循2D量子自旋霍尔效应的原则,科学家们提出了一种3D拓扑绝缘体[15],并在实验中观测到了其特征:位于体能带能隙中的Dirac型表面态色散[16].2011年,哈佛大学Fu[17]提出可通过晶格对称性构造一种三维拓扑晶体绝缘体.不同于一般拓扑绝缘体,其不需要自旋轨道耦合,拓扑性质受到晶格对称性(比如镜面对称性)而非时间反演对称性保护,并随后在实验上得以证实[18].2011年,南京大学Wan等[19]考虑Dirac方程对称性破缺后的Weyl方程,提出并设计了一类拓扑半金属材料,即Weyl半金属.另外,一类以准能量和时间周期性Floquet定理为标志的Floquet拓扑绝缘体也通过电磁波诱导得以实验实现[20].

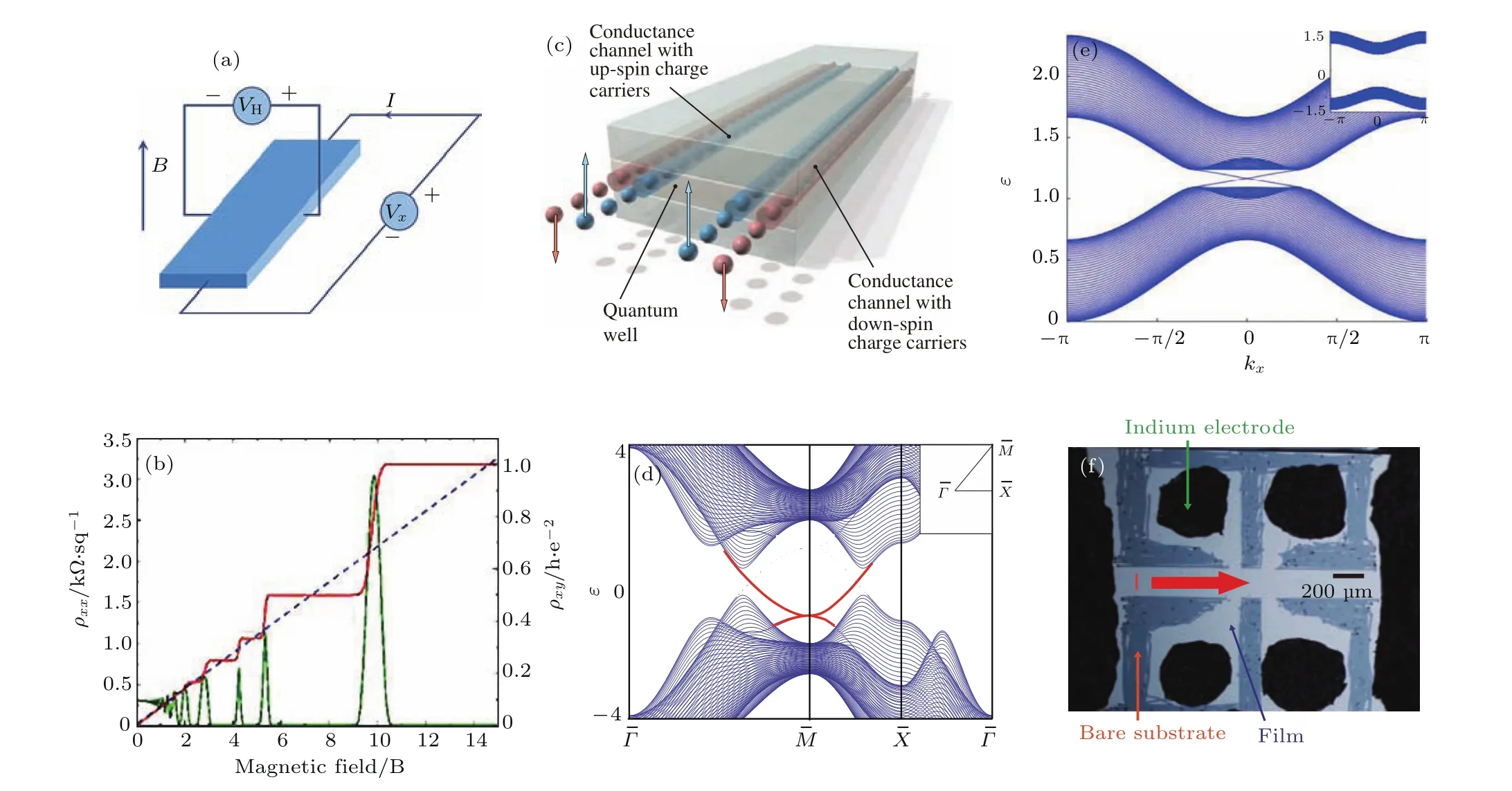
图3 霍尔效应家族(a)霍尔效应;(b)整数量子霍尔效应[7];(c)量子自旋霍尔效应[12];(d)拓扑晶绝缘体[17];(e)Floquet拓扑绝缘体[20];(f)反常量子霍尔效应实验[21]Fig.3.Hall e ff ect family:(a)Hall e ff ect;(b)integer quantum Hall e ff ect[7];(c)quantum spin Hall e ff ect[12];(d)topological crystalline insulators[17];(e)Floquet topological insulator[20];(f)the experiment of anomalous quantum Hall e ff ect[21].

然而,拓扑材料从理论到实践的跨越异常艰难.由于电子体系本身情况复杂,杂质影响难以忽略,而且能带论所要求的单电子假设不可能完美实现,所以前面提到的种种优美的物理现象很难在实验中轻易观测到.以量子反常霍尔效应为例,直到2013年,清华大学的Xue教授研究组[21]才在实验中观测到这一效应,据Haldane提出这一现象已经过去了25年.而另一方面,人工带隙材料——包括光子晶体声子晶体等——因为其玻色子相互作用弱,是一类纯净的系统.人工带隙材料具有更易制备的平台、更易于调控的能带结构,因而受到人们的重视.作为人工带隙材料的重要代表,光/声子晶体是把光/声介质材料按照周期性排列成晶格状得到的材料体系,其中的光/声流完全类似于电子系统中的电流.利用这种人工周期性系统实现电子能带拓扑性质具有可行性:1)能带的形成来源于晶格的平移对称性;2)量子化现象的本质来源于能带拓扑性质.电子系统本身特有的费米统计对电子能带拓扑现象并无影响.于是可以考虑利用声/光子晶体实现量子化的拓扑态.不仅如此,用人工带隙材料实现拓扑性质,具有自身独到的优点:1)人工带隙材料通常为玻色系统,于是可以无视电子系统中费米能级的限制,选取最合适的频段进行研究;2)在声光系统中,可以更方便准确地引入杂质或者无序,大大提高了实验灵活性;3)从实验的角度来看,光声系统具有更高的加工精度,因此可以进行更精准的调控[22];4)相比电子系统,光子和声子系统更容易实现高时空分辨的振幅和相位测量.

本文简要介绍几种具有代表性的光/声拓扑材料,并在理论上阐释拓扑现象的产生根源,从数学角度简要探讨拓扑材料产生的物理机理;首先介绍具有拓扑保护边界态的光/声整数量子霍尔效应;接着介绍具有成对出现的拓扑保护自旋流的光/声量子自旋霍尔效应;然后,以光/声Floquet拓扑绝缘体为代表,介绍具有不同形式边界态的拓扑材料;再拓展到介绍一维、三维的光/声拓扑材料;作为深化总结,从数学角度简要探讨拓扑材料产生的物理机理;最后是总结与展望.

2 光/声整数量子霍尔效应

先来回顾拓扑现象.拓扑材料往往具有不导电的体态,以及可以导电的表面态或者边界态.就像一个绝缘的陶瓷杯,表面镀了一层金,便具有了表面的导电性.不过,这两者有着本质的不同,拓扑材料的表面特性源于材料的内禀性质,缺陷和杂质都不会影响它.宛如静水流深却又波涛汹涌的海面,内里波澜不惊,表面上却可以风起云涌.而电流导通与否的本质在于能带.提取出系统中所有的可以存在的布洛赫波模式的波矢和频率,可以构成一个二维色散图,这就是能带,如图4(a)所示.可以看到,图中有些频率不对应任何模式,也就是说系统不允许这个频段的波通过,这就是带隙.对于材料内运动的电子,如果其频率刚好在这个带隙以内,那么就相当于进入了一个“绝缘体”,不会产生电流.然而,真实的材料具有表面,有些时候波可以在材料表面传播.这种表面态在能带上体现为一些孤立的色散曲线.如果系统参数选择得当,将会存在一种非常特殊的表面态色散:它联通了上下两段体态能带,贯穿了整个能隙,如图4(b)所示.

具有这种特征的表面态色散往往具有拓扑特征.在这条表面态色散曲线以下的体态色散曲线,构成了类似“面包圈”的非平庸拓扑能带.如果用一个特征指标来描述,可以说其“陈数”为1.而这条贯穿体态能隙的表面态色散,就像被上下体能带分别牵住了两头,相对小的参数调整都不会让它断开.回到体系导通性质上,就会看到刚好处于体能带带隙中的波输入材料时,无法在体块内部传播,但是可以在表面传播.不仅如此,表面上的加工不均匀,或者形貌弯折,都不会改变材料的拓扑性质,也就不会改变这个表面态的传输.这就是整数量子霍尔效应所具有的“鲁棒”边界态.对应的材料,被称为“陈拓扑绝缘体”.

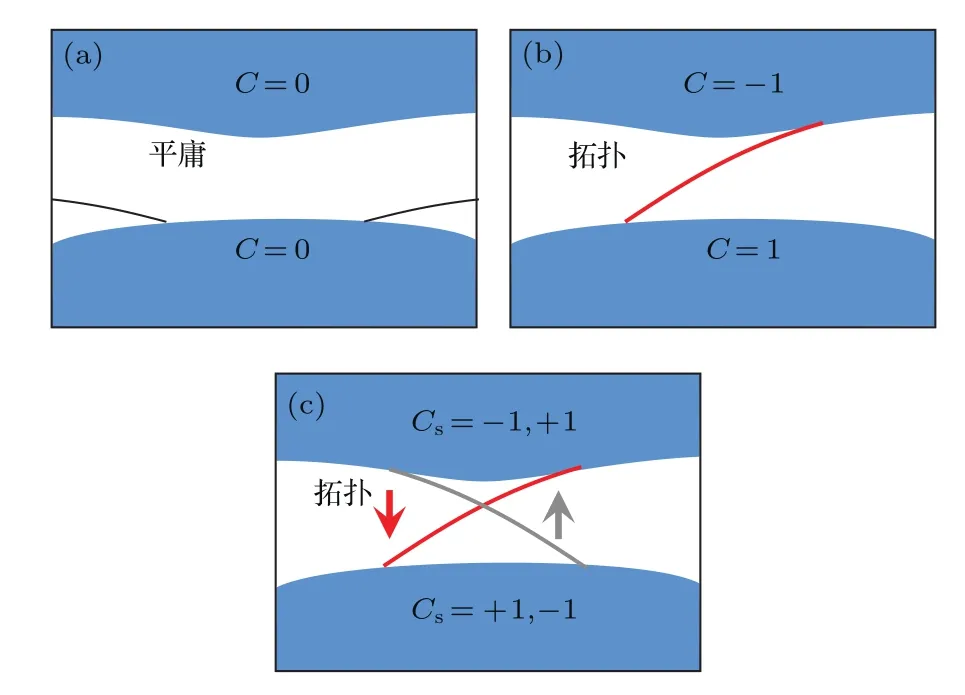
图4 (a)能隙与平庸边界态;(b)整数量子霍尔效应中的拓扑边界态;(c)量子自旋霍尔效应中的拓扑边界态Fig.4.(a)Band gap and trivial edge state;(b)the topological state of integral quantum Hall e ff ect;(c)the topological state of quantum spin Hall e ff ect.

回到我们关注的光/声系统中来.由于同样具有周期性结构,光子晶体/声子晶体中光/声的色散曲线同样会构成“能带”.那么在光/声系统中能否实现拓扑呢?2005年,Haldane和Raghu[23]首次提出了光子晶体领域的量子拓扑现象.他们在理论上指出,应该首先在能带中构造Dirac简并,即色散关系满足无质量Dirac方程,而后在方程中添加质量项使简并破缺,方能实现光量子霍尔效应.破缺对称的方式包括破坏系统空间反演对称性,以及时间反演对称性.经过计算,他们发现,只有当打破时间反演对称性时,两个不等价Dirac点才会具有符号相同的Berry curvatures(可以视为陈数在整个布里渊区随波矢k的分布).于是,可以使得整条能带具有非零的陈数.反之,破缺空间反演对称性,而保持时间反演不变性的系统,Berry curvatures符号相反,能带具有的陈数将会互相抵消.

2008年,Wang等[24]绕开了构造Dirac简并的步骤,直接破缺系统二次简并,提出了实现光量子霍尔效应的具体方案.他们引入各向异性,给系统的介电常数矩阵ε引入了含有虚部的非对角项.这种含有虚部的非对角项对应于一个等效磁场,遵循了Haldane提出的破缺时间反演对称性的原则.值得一提的是,两篇论文为了实现非零陈数,都利用了含质量项的Dirac方程,区别仅在于破缺对称性方式不同.基于Wang等在2008年的设计实验,麻省理工学院课题组在实验上利用金属墙包围的旋磁光子晶体介质材料首次观测到了单通拓扑光子态,如图5(a)所示[25].类似电子系统的量子霍尔效应,这种单通光子态传播时对各种障碍物及缺陷无散射,即具有鲁棒特性.此外,如果调整这种边界态落在空气线以外,就会形成无需金属介质限制的边界模式[26].这一单通效应很快在其他诸多平台上得以实现,例如耦合腔(coupled cavities)[27]、旋磁光子晶体板(gyromagnetic photonic crystal slab)[28]以及超光子簇(gyrotropic photonic clusters)[29]等.值得注意的是,破缺简并点的个数将会直接影响边界态的个数[30].

相比之下,声学量子霍尔效应研究起步较晚.这是因为陈拓扑绝缘体要求时间反演破缺,而声场受磁场影响较小,难以在其中引入时间反演破缺.如图5(b)所示,2014年,Alu等[31]巧妙地在声波环形腔中引入了气流,实现了声学隔离器.在他们的设计中,不同运动方向的环形腔模式感受到的气流影响正类似于不同自旋感受到的磁场影响.这给了人们很多启示:是否可以将气流等效视为声学系统中的磁势场呢?2016年,Yang等[32]以及Ni等[33]分别考虑在环形腔中引入气流作为等效势场,破缺了时间反演对称性,从而实现了声学陈绝缘体.

图5 (a)实验实现光子晶体量子霍尔效应[25];(b)在声学环形腔中引入气流作为等效势场[31]Fig.5.(a)Experimental realization of photonic quantum Hall e ff ect[25];(b)introducing air flow as e ff ective potential field in the acoustic annular cavity[31].

3 光/声量子自旋霍尔效应

中国古代讲究太极阴阳调和,剑法中也有君子剑淑女剑双剑合璧.类似地,凝聚态系统中,电子也具有成对的“自旋”这个内禀属性.如果在系统中引入自旋轨道耦合,那么两种不同自旋的电子,将会“感受”到两个相反方向的磁场.对应地,拓扑材料表面将会形成一对流向相反的边界态,分别对应两种自旋.2005年和2006年,Kane和Zhang等分别提出,利用电子强自旋轨道耦合,可以在零磁场下得到一对共轭的自旋相反的无能隙边界态.这一对自旋相反的共轭态能流大小相等方向相反,分别满足一对共轭的含质量项Dirac方程.在能带上看,这对边界态将会在布里渊区中心发生简并,如图4(c)所示.与整数量子霍尔效应不同的是,这种量子自旋霍尔效应,需要保持时间反演对称性来保证边界态的鲁棒特性.

同样地,光子也具有自旋.除去自旋为零的虚光子态,光子本征值为正负一的自旋态分别对应的左右旋光态刚好可以构成一对共轭态.实际上,可以在光/声玻色系统中找到多种类似左右旋光这样成对的态——称之为“赝自旋”态——进而考虑研究光/声量子自旋霍尔效应.量子自旋霍尔效应的核心效应是成对出现的受到时间反演对称性保护的鲁棒拓扑边界态,其关键是实现边界态在能隙中的简并,即Kramers简并.电子作为费米子,时间反演对称性刚好可以使之满足这一简并条件.而光和声作为玻色系统,其时间反演对称性与作为费米子的电子有本质的不同,无法构造Kramers简并.这一现状给科学家以启发:如果时间反演对称性不能在玻色系统中构造Kramers简并,那么其他对称性能否构造Kramers简并?换言之,在玻色系统中实现量子自旋霍尔效应,其鲁棒特性是否必须由时间反演对称性保护?

2013年,德克萨斯大学奥斯汀分校Khanikaev等[34]在理论上提出了一种利用双各向异性介质实现的二维光拓扑绝缘体,如图6所示.他们构造了六角晶格,并采用在高对称点附近TE+TE/TETM线偏振作为赝自旋态.这篇文章提到的系统的确具有时间反演对称性,且作者也证明了系统的鲁棒特性.但是,他们并没有验证系统鲁棒特性与对称性的一一对应关系,也就是说,这种鲁棒特性是否与时间反演对称性直接相关仍然存疑.2014年,南京大学卢明辉、陈延峰研究小组在arXiv上撰文,理论上提出了一种基于压电/压磁超晶格构成的光拓扑绝缘体模型.作者采用四方晶格,并且以左右旋光LCP/RCP为赝自旋对.与文献[34]的模型不同,该系统破缺时间反演,仅保留一种电磁对偶与时间反演叠加的对称性——称之为赝时间反演对称性.作者系统地论证了这种鲁棒特性实际上是受到赝时间反演对称性保护的,而时间反演对称的存在,只是用来描述“磁场”或者“内禀磁矩”的影响.至此,抛开了玻色子时间反演对称性的约束,可以采用多种自由度角度进行研究,从而可以在玻色系统中构造更易于实现和调控的新型拓扑光子态.该文章于2016年正式发表[35].

在实验方面,2014年,中山大学董建文教授课题组验证了此类拓扑边界态的传输特性[36].他们利用星形和圆盘形超构材料构造匹配参数在微波频段观测到了以TE+TE/TE-TM线偏振作为赝自旋态量子自旋霍尔效应.

图6 光拓扑绝缘体 (a)以TE+TM/TE-TM为赝自旋的时间反演对称保持的光拓扑绝缘体[34];(b)以LCP/RCP为自旋的时间反演对称破缺的光拓扑绝缘体[35]Fig.6.Photonic topological insulator:(a)Photonic topological insulator taking TE+TM/TE-TM modes as pseudospin with time-reversal symmetry[34];(b)photonic topological insulator taking LCP/RCP modes as pseudospin with no time-reversal symmetry[35].

通过上述文献,已经发现,构造量子自旋霍尔效应的关键在于赝时间反演对称性.基于此原理,甚至可以考虑让空间点群对称性来扮演这个角色.

2015年,日本NIMS研究人员Hu等[37]在理论上提出可通过复式六方晶格中的C6v对称性在各向同性介质材料中构造出光量子自旋霍尔态.其赝时间反演对称性来自晶格的对称性,对称操作包括旋转60◦和120◦组合等.他们利用能带的折叠,将本来处于布里渊区顶点的Dirac简并折叠至布里渊区中心,从而形成双重Dirac点(取非初基元胞),如图7(a)所示.而通过从拉伸到压缩晶格的过程,可实现p轨道和d轨道间的能带反转,使能带经历从Dirac点简并到破缺的过程,如图7(b)所示.在简并破缺后的体能带能隙中,可以观测到以杂化轨道为赝自旋的鲁棒自旋边界态.该设计不同于之前工作需要考虑复杂的偏振耦合,仅仅利用纯介电光子晶体就可以构造光拓扑绝缘体,因而更容易在实际中得到应用.

需要指出的是,这种拓扑模型利用的是二维平面内的晶体对称性,因此可以看作3D拓扑晶体绝缘体[17](将在下一章介绍)在2D情况的推广.虽然它具有非平庸的体拓扑数,但由于波导左右两边布洛赫态并不完全相同,所以其边界态在理论上讲并不是完全无能隙的.因此,严格地讲,背散射只是被抑制并不是完全免疫.但此模型微带隙可根据需要调节得无限小,因而能够满足应用需要.

除此之外,这种构造赝时间反演对称性的思路,还被拓展到了机械学[39]、声学等领域,为QSH的多平台实现提供了有力的工具.2016年,南京大学卢明辉、陈延峰小组在实验上验证了基于声子晶体偶然简并的双重狄拉克点附近的能带反转构造声学量子自旋霍尔效应[38].该系统选择pd波的不同线性组合作为两种赝自旋.但是不同于文献[37]的能带折叠机理,该系统提供了一种通过调节占空比实现Dirac点由简并到破缺的过程.实验证明,在该系统具有鲁棒特性,声波在波导中的传播体现出具有背散射抑制现象.这是在实验上首次实现的声学量子自旋霍尔效应模型.特别值得一提的是,该文解决了拓扑绝缘体经常面临的单一自旋声源制备困难问题,十分巧妙地构造了一种“X”型分路器模型,在空间上自然分离出两类赝自旋声子,如图7(c)所示.

图7 (a)六角晶格结构;(b)K,K′点的简并折叠到Γ点上,并且随着元胞内原子间距的调整,d/p波能带反转[37];(c)声学量子自旋霍尔效应分路器[38]Fig.7.(a)Hexagonal lattice;(b)Energy band folding.d/p band inversion with the increasing of the distance between atoms[37];(c)Cross-waveguide splitter realized by topological phononic crystals[38].

4 光/声Floquet拓扑绝缘体

人工带隙材料是一门善于学习的学科.既然电子系统中有自旋,那么就可以有光/声赝自旋;有时间反演对称性,就可以有“赝时间反演对称性”.同样,对于整数量子霍尔效应中破坏时间反演对称性的磁场,可以考虑一种具有同样效果的“赝磁场”,或者说由引入等效矢势的方式获得的有效磁场.由于引入有效势的方式往往要用到周期调制,而周期调制的系统,其运动方程满足Floquet原理(例如固体物理中的Bloch波,就是Floquet定理的直接结论),并且这种系统在能带上具有准能量的特征,所以将其统一归类为Floquet拓扑绝缘体[20].

2012年,斯坦福大学Fan研究组理论上指出:可以利用光相位动态调制的方法来实现有效磁场,认为破缺时间反演,达到破缺Dirac简并的目的[40,41].他们提出(如图8(a)所示),用含时调制的方法,使得两个具有不同共振频率小球间横向不耦合,而纵向耦合相位随周期数线性增加.如此一来,光经过一个小元格(plaquette)后将会获得一个相位ϕ,也就相当于经历了一个有效规范势.利用AB效应原理,这等效于一个规范磁场

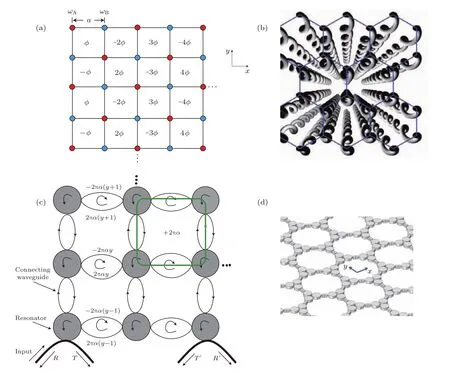
图8 (a)通过时间调制引入有效势[41];(b)通过空间调制引入有效势[42];(c)耦合共振腔结构实现鲁棒的光学拓扑延迟线的理论设计[43];(d)声学Floquet拓扑绝缘体[58]Fig.8.(a)Introducing e ff ective potential with time modulation[41];(b)introducing e ff ective potential with spatial modulation[42];(c)theoretical design of robust optical delay lines with coupled resonator optical waveguides[43];(d)phononic Floquet topological insulator[58].

在上述系统中,耦合强度随时间成周期性变化V(t)=Vcos(Ωt+ϕij),其中ϕij为相位因子.此时整个系统随时间呈现周期性变化,其哈密顿量满足H(t+T)=H(t),T=2π/Ω,满足Floquet定理的应用条件.于是其波函数可写为ψ(t)=e−iεtϕ(t),其中ϕ(t)=ϕ(t+T)满足周期性(类比于布洛赫定理中随坐标空间周期性变化). 于是,可以把ε视为准能量,且满足(H(t)− iI∂t)ϕ(t)=εϕ(t). 由此可以得到准能量动量空间的体能带.进一步分析可以发现,能带的运动方程又是含有质量项的Dirac方程(有效势刚好提供了质量项).进一步分析其拓扑性质,得到无能隙的拓扑边界态.

然而,实现耦合强度周期性的准确含时调制在实验上有一定难度.2013年,以色列理工学院Rechtsman等[42]提出了一种方案,以空间维度上的周期性几何调制(z方向)来代替时间的周期调制,并在实验上实现了光Floquet拓扑绝缘体,如图8(b)所示.这个模型属于3D光子系统,在下一节中会进一步介绍.但是,这种构造Floquet定理的设计方式给了2D系统很重要的启发.

2011年,美国马里兰大学Hafezi等[43,44]理论设计,并随后(2013年)在实验上实现了一种环形微腔中的单向边界传播态[43,44].他们把顺时针和逆时针传播模式为赝自旋,如图8(c)所示.顺(逆)时针传播模式经过一个小元格会产生符号相反的有效规范势.实验上证实,该模型中通讯波段光(1539 nm)具有单向传输和背散射抑制的鲁棒特性.之后的研究表明,这种基于共振耦合微腔的结构可以对应于准能量动量系统,从而完全对应于网格模型下的Floquet拓扑绝缘体[45].此外,基于这种有效场理论或者网络模型的其他Floquet拓扑绝缘体设计被不断提出[46−57].

对于声学系统,同样可以考虑时间调制,或者设计网格模型,利用顺时针、逆时针的声学传播模式构造声赝自旋.但是,与光学不同,声学材料阻抗失配较大,导致耦合系数极低,在实验上较难观测到明显现象.因此,需要较高的加工精度来支持声学实验.如图8(d)所示,2016年,Alú等[58]利用时间调制声学晶格,在理论和模拟上提出了声学Floquet效应.紧接着,利用网格模型的水声环耦合模型[59]以及超构材料波导耦合模型相继提出,在实验上实现了声学Floquet拓扑绝缘体[60].

5 一维/三维的光/声拓扑材料

本文开篇以湖面飞剑场景,简单描述了拓扑边界态的性质.实际上,这个场景更像是在描述3D拓扑绝缘体的表面态.除了最初获得成功的2D系统,科学家们也对其他维度,例如1D/3D拓扑材料进行了研究.可以从前面讨论过的二维系统,以及贯穿其中的Dirac方程出发,对1D/3D系统进行分类.

对于1D系统,首先,把2D系统向1D投影,可以得到“1D准周期系统”,其模型包括:Haper(Aubry-Andre)模型[61,62],以及对角Fibonacci模型[63]等.通过引入特定分布的势场,可以在1D结构中构造满足要求的紧束缚近似模型.2012,Kraus等[64]理论计算并实验验证了一维准晶系统表现出具有拓扑保护性质的边界态,其拓扑不变量可以视为2D陈数的投影.2013年,Verbin等[65]利用1D光学晶格实现准晶系统,观测到了拓扑相变,其实验激光位于红外波段,如图9(a)所示.

图9 1D拓扑系统 (a)一维光学晶格准晶拓扑系统[65];(b)一维光子晶体中的Zak相位[69];(c)等离激元Majorana费米子[71]Fig.9.1D topological system:(a)Quasi-crystal topology system in 1D photonic crystal[65];(b)Zak phase in 1D photonic crystal[69];(c)plasmonic Majorana Fermions[71].

其次,把2D几何相位陈数向1D推广就得到了Zak相位[66],代表性的模型是SSH模型[67].2014年,香港科技大学的陈子亭研究小组通过调节结构参数光学构造阻抗匹配,理论上实现几何相位控制的拓扑边界态[68].2015年,他们又在声学领域取得突破,从理论上和实验上提出了收到Zak相位控制的声学一维拓扑边界态[69],如图9(b)所示.

最后,把视线退回到Dirac方程的本源,选取不同的表象,可以得到Dirac费米子、Weyl费米子、或者Majorana费米子.其中Weyl费米子将在三维系统中详细描述,而Majorana费米子对应的Kitaev模型[70],可以在1D系统中实现.2014年,Poddubny等[71]利用纳米颗粒组成“zigzag”型阵列,根据入射光极化方向的不同,激发了不同的等离激元模式,进而得到了不同的边界模式,如图9(c)所示.

对于3维系统,仍然从Dirac方程出发来考察.首先,一个最直接的思路是:在三维系统中构造2D Dirac方程.于是可以利用2D系统中的各种结论进一步分析三维系统,这就是前面提到过的Floquet拓扑绝缘体[20,42].如图10(a)所示,利用螺旋形波导管组成六角晶格,并用空间坐标Z等效地代替时间左边,从而构造了含有等效势场的运动方程

图10 (a)光学Floquet拓扑绝缘体[42];(b)利用晶格对称性实现光学Dirac点[73];(c)光学Weyl点[75]Fig.10.(a)Photonic Floquet topological insulator[42];(b)realizing photonic Dirac point with lattice symmetry[73];(c)photonic Weyl point[75].

其中,矢势项

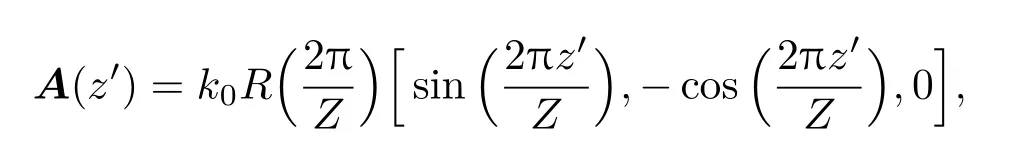
可具有有效磁场Beff=∇×A.而其中ψ′是z方向的周期函数,可用Floquet定理表示为ψ′(z′)=e−iεtψ′(z′).同理, 准能量可表示为Bloch波矢(kx,ky)的函数,即Floquet能带图.那么,则可得到无能隙的拓扑边界态.实验表明,光(633 nm)可沿z方向绕其边界无背散射传播(单向螺旋上升),具有一定的缺陷免疫能力.

另一方面,上述这种用空间代替时间的方式启发我们重新审视时间反演对称性在整个系统中扮演的角色,考虑是否可以用其他对称性取代其位置,于是就有了拓扑晶绝缘体的概念[17].在2D系统中,已经看到了取代时间反演对称性的赝时间反演对称性取得的成果[39,37,38].对于3D系统,在2016年,麻省理工学院Lu等[72]提出了一种受到晶体对称性——非点群滑移反射保护,而非时间反演对称性保护的表面态Dirac点.他们给铁磁材料施加外磁场打开了体能带带隙,可以在微波段实现3D光拓扑绝缘体.同年,Jiang等[73]提出了利用全电介质材料实现点群保护的三维光拓扑绝缘体的方法,在能带中发现了成对出现的Dirac点,如图10(b)所示.

由于相较于2D系统增加了一个维度,3D Dirac点不同于2D Dirac点的独立出现,将会在倒空间中形成一个“线模式”(“line node”),在二维空间观察仍然是线性色散.仍然按照二维系统的思路,通过破缺对称性的方式试图打开简并.此时线模式退化,在三维空间中形成线性简并点——Weyl点.不同于二维的Dirac简并,此处的Berry曲率完全类似磁单极子磁场分布.即该点自带非零陈数,因而在该点处,系统具有丰富的拓扑物理性质[19].2013年,麻省理工学院Lu等[74,75]提出了利用gyroid材料实现光子Weyl点,并在随后的实验中观察到对应的现象,如图10(c)所示.在声学领域,2015年,香港科技大学陈子亭研究小组提出了一种堆叠状的声学模型.通过调控层间耦合参数,实现了三维声学Weyl点[76].进一步研究表明,前面研究的Weyl点,其色散关系的二维投影是椭圆.而Dirac点在退化为Weyl点是,可能形成双曲线形色散,这就是第二类Weyl点.对应的光学声学拓扑系统也已经先后被设计提出[77,78].

6 Dirac方程的拓扑性质

御剑之气从何而来?通过前面几章的讨论,我们发现,一个拓扑系统中往往隐藏着一个含有质量项的Dirac方程.实际上,Dirac方程正是拓扑效应的关键所在.这里将利用数学工具,详细讲解这一关系.首先从光/声动力学模型出发,得到Dirac方程.之后,分析Dirac方程所引发的边界态.最后,讨论Dirac方程所具有的拓扑性质,也就是几何相位.

6.1 从光/声系统到Dirac方程

首先来看他们的运动方程.

光学系统基本运动方程为Maxwell方程组.以二维系统为例,对于各向同性介质,相对介电常数和磁导率是于是运动方程表达式为

把Ez视为波函数ϕ,前面的运算视为哈密顿算子H,本征频率ω2/c2视为波函数本征值,可以得到一个等效的单电子哈密顿方程

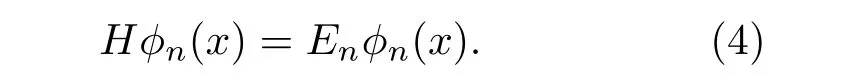
声学系统运动方程形式比较多样,但是同样可以写出一套与电子系统类似的单粒子运动方程,形式同上.

于是系统的波函数可以表示为

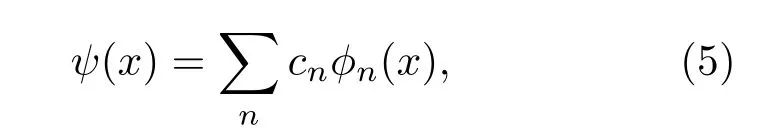
二次量子化使之成为算符.则系统的总哈密顿量可以表示为

我们把本征波函数取为每一个元胞内的本征波函数,并且只保留最近邻项就得到了二次量子化后的有效哈密顿量

其中i,j表示元胞位置,α,β表示元胞中的不同波函数.例如在石墨烯结构中,α,β代表同一晶格中两个不同原子的波函数;而在四方中,它们可以用来表示轨道角动量s波p波.对产生湮没算符进行傅里叶变换可以得到

其中δ代表最近邻的耦合.以一维系统为例,具体展示如何变换得到Dirac方程.一维原子链的耦合情况如图11所示.

图11 一维原子链Fig.11.1D chain of atoms

我们可以得到

其中

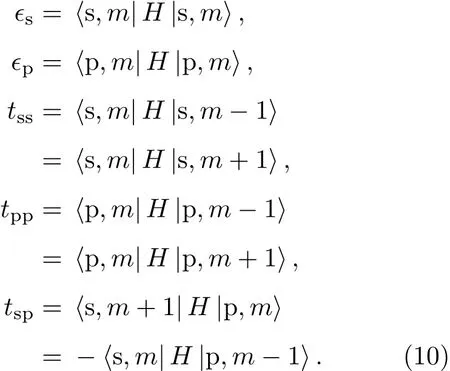
假设能带带隙围绕k=0点,可以把哈密顿量在k=0处展开到k的线性项,得到

这刚好是Dirac方程的基本形式.

下面考察Dirac方程的基本性质.

6.2 Dirac方程与边界态

1928年,Dirac提出了一个用于描述电子运动的相对论量子力学波动方程.

其中c代表光速,p是动量,m是粒子质量项,α和β是Dirac矩阵.由于必须满足质能方程,它们需要满足如下关系:

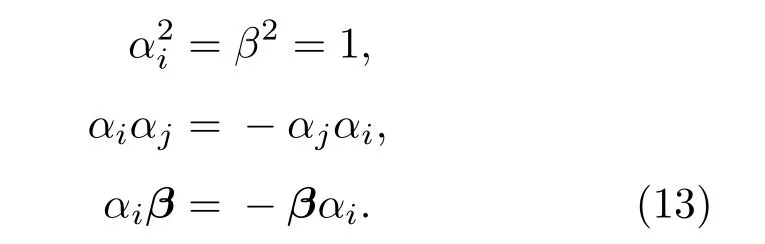
显然泡利矩阵满足上述关系

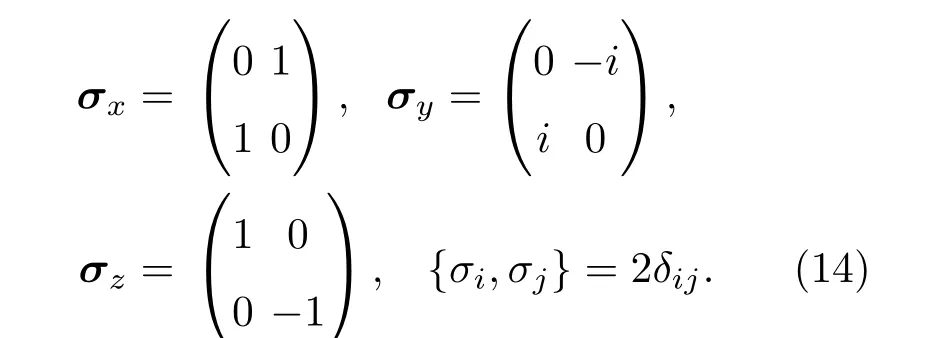
在一维和二维空间中,可以选择泡利矩阵作为Dirac矩阵.方便起见,一维情况可以取

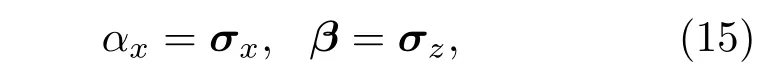
二维情况

然而,单纯的Dirac方程并不足以描述我们的问题.原因如下:1)假设我们的材料边界处于真空之中,如图12所示.对于真实的材料体系,需要在开放边界条件ψ(x=0)=0以及无限距离边界条件ψ(x=∞)=0,Dirac方程的解无法同时满足上述要求;2)对于单纯的Dirac方程,具有质量对称性,进行一个幺正变换之后,质量项符号可以变化,这使得拓扑平庸与非平庸的判断并不能仅仅基于特定参数m,而需要依赖另一个附加参数,这并不符合“拓扑是物质的内禀性质”的预期.于是,我们需要在质量项上增加一个动量的二次项来实现我们的目的,

在这里,把光速c换为粒子速度vf.这样首先打破了m进行幺正变换时可以变成−m的对称性,后面将会看到它会完全满足边界条件.

图12 (a)波函数在材料与真空环境的界面上,可以观测到一对运动方向相反的边界态,其对应能带如图(b)所示Fig.12.(a)Wave function in the interface between material and vacuum,there are a pair of edge states,which has di ff erent direction,the energy band is shown in(b).

对于一维情形

考虑能量E对应的本征解ψ,Hψ=Eψ.显然有Hτyψ=−τyHψ=−Eτyψ,也就是说,ψ′=τyψ将会是能量−E对应的本征解.我们发现系统总归会具有一个零能量解E=0.下面重点来考察这个特殊的零能量解(实际上,对于单纯Dirac方程,这也是边界态连续性的要求).代入试探解ψ(x)～eλxξ,其中ξ是与x无关的二分量波函数,于是得到

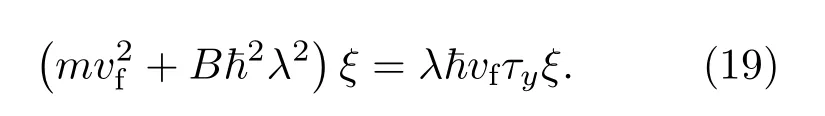
于是ξ必须是τy的本征波矢τyξs=sξ(s=±1).对应的λ可以求解得到

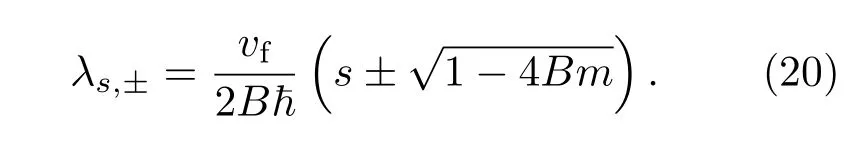
利用边界条件ψ(x=0)=0,解的一般形式可以写作

再利用边界条件ψ(x→∞)→0,需要λs,±＜0或者λs,±＞0此时λ−s,±＜0.这就等价于这就是拓扑现象中经常提到的“能带反转”.在这个条件下,可以得到

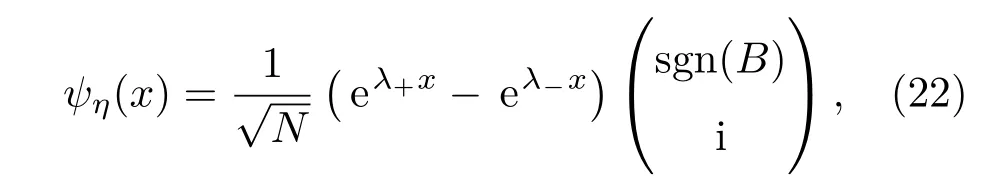
下面考虑二维情形.先讨论量子反常霍尔效应模型(quantum anomalous Hall e ff ect,QAH),因为量子自旋霍尔效应实际上可以视为两个QAH模型的叠加.

把方程HQAHψ(x)=Eψ(x)分离变量可以得到

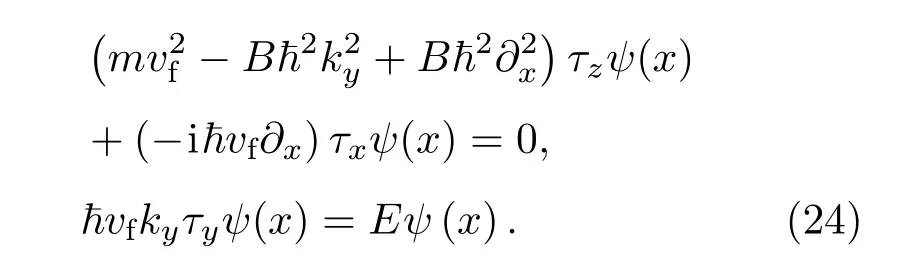
然而,此时必须保证第二式与第一式同时成立.好在第二式与第一式一样,要求ψ是σy的本征波函数,于是,可以把一维情况下的解原样复制到二维情况.

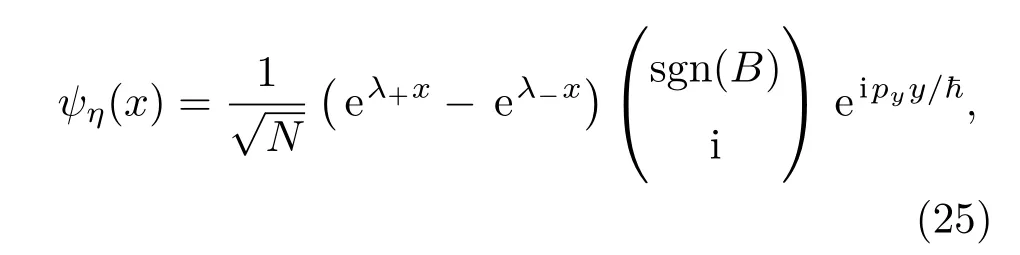
下面把这段推导推广到量子自旋霍尔效应.

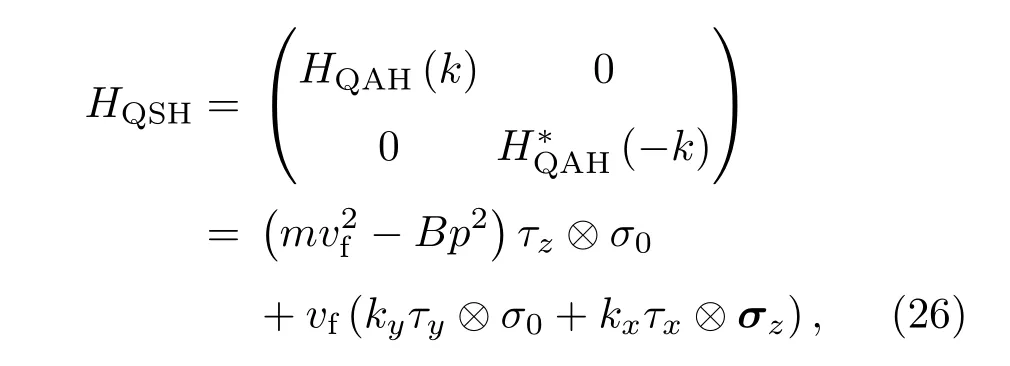
那么对应的解为

色散关系为

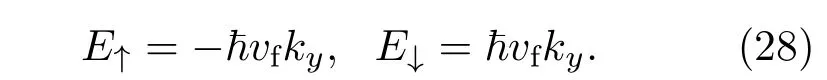
这一对边界态的传播方向与自旋方向相互锁定,称为“螺旋边界态”(helical edge state).

6.3 Dirac方程的几何相位

综上我们发现,通过Dirac方程可以得到一个螺旋性的边界态,并且把Dirac方程与我们熟悉的晶格运动方程联系了起来.下面,分别用TKNN方法,以及Dirac运动方程,考察这个边界态的拓扑性质.

对于周期性晶格结构,有

其中,un,k(r)=un,k(r+R).把H(r)展开到k空间H(r)=e−ik·rH(r)eik·r有

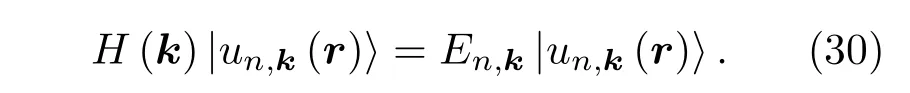
利用TKNN方法可以得到霍尔电导率表示为

其中α,β代表方向指标,引入一个矢势A,其分量满足

对应的场强(也就是Berry曲率)

于是霍尔电导率可以表示为

而在数学上,积分项刚好对应“陈数”,

于是霍尔电导率可以表示为

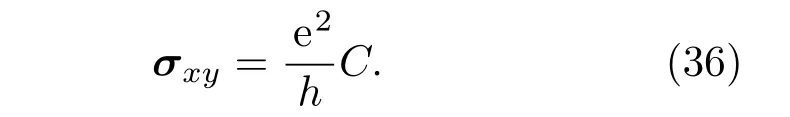
而另一方面,从Dirac方程出发,霍尔电导率可以表示为

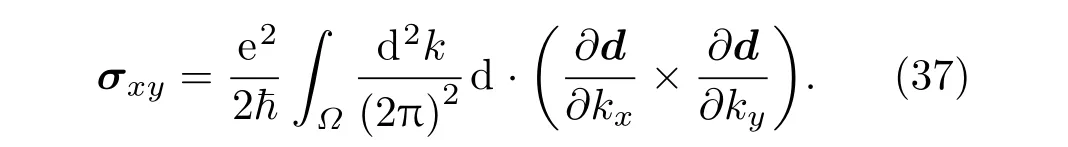
其中d是狄拉克方程中的各个分量,

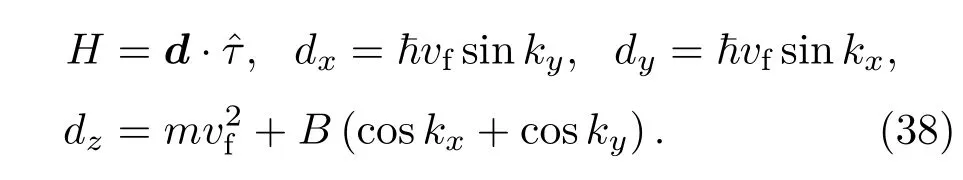
进一步推导可得

当mB＞0时,C0此时存在拓扑非平庸边界态;当mB＜0时,C=0,此时系统处于拓扑平庸状态.上述推导与之前得出的边界态存在条件完全一致.于是,我们从Dirac方程出发,得出了与TKNN方法一样的霍尔电导率,更进一步证明了可以通过分析Dirac方程,预测系统的拓扑性质.

7 总结与展望

拓扑人工带隙材料因其独特的鲁棒边界态越来越多地受到人们的关注.本文简要撷取了近年来备受关注的研究方向,包括光/声整数量子霍尔效应,量子自旋霍尔效应,Floquet拓扑绝缘体以及1维/3维拓扑系统等.我们对这些现象进行了简要的描述,并且列举了相应的具有代表性的研究成果.除此之外,在第六章对这种拓扑性质的由来进行了理论探讨,说明了Dirac方程可以视为拓扑现象的产生根源.

鲁棒边界态具有免疫缺陷、背散射抑制、性能稳定等优异特性,具有巨大的潜在应用价值.首先,利用拓扑材料制成的光/声器件,将会具有极高的信噪比,大大提高器件性能;其次,由于免疫缺陷,拓扑材料对加工精度的要求并不苛刻,科学家对光/声器件的研究不再强烈依赖极端的实验室环境,这便于产业推广以及实验室普及;最后,由于传输性能稳定,科学家们可以放开思路,把研究的重点转移到其他原本受到稳定性限制的新性能研究上.例如纠缠或非线性效应作用下光/声拓扑态的情况、拓扑保护的单向传播光子晶体光纤、光量子计算等.

理论研究方面,后续的拓扑研究工作可以全面围绕Dirac方程展开.作为连接量子力学与相对论的重要纽带,Dirac方程具有多种表象,对应各种不同的解的形式,包括Weyl费米子、Majorana费米子、Dirac费米子等.考虑到人工带隙材料的可设计性、可调谐、不易受杂质影响等特性,可以把它作为实验平台,实现这些电子系统中虽有预言、但是难以获得的准粒子.另一方面,Dirac方程对应的简并与简并破缺,直接影响了能带的拓扑性质,或者说几何相位.以往的拓扑学分析,通常要求系统具有厄米性质,且往往局限于单粒子方程.我们可以试图在理论上将Dirac方程与几何相位推广到非厄米体系,或者多粒子体系.如在拓扑声/光学系统中引入增益损耗,实现具有实本征值的非厄米系统,或者引入非线性参数,构造相互作用模型等.

综上所述,进行人工带隙材料拓扑性质的研究无论是对理论研究发展,还是对于最终转化为实际产品都有着重要指导作用.光/声子晶体拓扑态及其相关领域的研究对未来拓扑光/声子学的发展具有里程碑式的意义,终将成为现代光/声子学里的一个重要组成部分.

[1]Pancharatnam S 1956Proc.Indian Acad.Sci.Sect.A44 398

[2]Berry M V 1984Proc.Royal Soci.London A:Math.Phys.Engineer.Sci.392 45

[3]Tomita A,Chiao R Y 1986Phys.Rev.Lett.57 937

[4]Asorey M 2016Nat.Phys.12 616

[5] “The 2016 Nobel Prize in Physics-Press Release.” from http://www.nobelprize.org/nobel_prizes/physics/laureates/2016/press.html.

[6]Hall E H 1879Am.J.Math.2 287

[7]Klitzing K V,Dorda G,Pepper M 1980Phys.Rev.Lett.45 494

[8]Thouless D J,Kohmoto M,Nightingale M P,den Nijs M 1982Phys.Rev.Lett.49 405

[9]Haldane F D M 1988Phys.Rev.Lett.61 2015

[10]Shen S Q 2012Topological Insulator.(Springer,Berlin)

[11]Bernevig B A,Hughes T L,Zhang S C 2006Science314 1757

[12]König M,Wiedmann S,Brüne C,Roth A,Buhmann H,Molenkamp L W,Qi X L,Zhang S C 2007Science318 766

[13]Kane C L,Mele E J 2005Phys.Rev.Lett.95 146802

[14]Sheng L,Sheng D N,Ting C S,Haldane F D M 2005Phys.Rev.Lett.95 136602

[15]Zhang H J,Liu C X,Qi X L,Dai X,Fang Z,Zhang S C 2009Nat.Phys.5 438

[16]Chen Y L,Analytis J G,Chu J H,Liu Z K,Mo S K,Qi X L,Zhang H J,Lu D H,Dai X,Fang Z,Zhang S C,Fisher I R,Hussain Z,Shen Z X 2009Science325 178

[17]Fu L 2011Phys.Rev.Lett.106 106802

[18]Hsieh T H,Lin H,Liu J,Duan W,Bansil A,Fu L 2012Nat.Commun.3982

[19]Wan X,Turner A M,Vishwanath A,Savrasov S Y 2011Phys.Rev.B83 205101

[20]Cayssol J,Dora B,Simon F,Moessner R 2013Phys.Status Solidi Rapid Res.Lett.7101

[21]Chang C Z,Zhang J,Feng X,Shen J,Zhang Z,Guo M,Li K,Ou Y,Wei P,Wang L L,Ji Z Q,Feng Y,Ji S,Chen X,Jia J,Dai X,Fang Z,Zhang S C,He K,Wang Y,Lu L,Ma X C,Xue Q K 2013Science340 167

[22]Lu L,Joannopoulos J D,Soljacic M 2016Nat.Phys.12 626

[23]Haldane F D M,Raghu S 2008Phys.Rev.Lett.100 013904

[24]Wang Z,Chong Y D,Joannopoulos J D,Soljacic M 2008Phys.Rev.Lett.100 013905

[25]Wang Z,Chong Y,Joannopoulos J D,Soljacic M 2009Nature461 772

[26]Poo Y,Wu R X,Lin Z,Yang Y,Chan C T 2011Phys.Rev.Lett.106 093903

[27]Yannopapas V 2011Phys.Rev.B84 195126

[28]Liu K,Shen L,He S 2012Opt.Lett.37 4110

[29]Asatryan A A,Botten L C,Fang K,Fan S,McPhedran R C 2013Phys.Rev.B88 035127

[30]Skirlo S A,Lu L,Igarashi Y,Yan Q,Joannopoulos J,Soljačić M 2015Phys.Rev.Lett.115 253901

[31]Fleury R,Sounas D L,Sieck C F,Haberman M R,Alù A 2014Science343 516

[32]Yang Z,Gao F,Shi X,Lin X,Gao Z,Chong Y,Zhang B 2015Phys.Rev.Lett.114 114301

[33]Ni X,He C,Sun X C,Liu X P,Lu M H,Feng L,Chen Y F 2015New J.Phys.17 053016

[34]Khanikaev A B,Mousavi S H,Tse W K,Kargarian M,MacDonald A H,Shvets G 2013Nat.Mater.12 233

[35]He C,Sun X C,Liu X P,Lu M H,Chen Y,Feng L,Chen Y F 2016Proc.Natl.Acad.Sci.USA113 4924

[36]Chen W J,Jiang S J,Chen X D,Zhu B,Zhou L,Dong J W,Chan C T 2014Nat.Commun.5 5782

[37]Wu L H,Hu X 2015Phys.Rev.Lett.114 223901

[38]He C,Ni X,Ge H,Sun X C,Chen Y B,Lu M H,Liu X P,Chen Y F 2016Nat.Phys.12 1124

[39]Susstrunk R,Huber S D 2015Science349 47

[40]Fang K,Yu Z,Fan S 2012Phys.Rev.Lett.108 153901

[41]Fang K,Yu Z,Fan S 2012Nat.Photon.6 782

[42]Rechtsman M C,Zeuner J M,Plotnik Y,Lumer Y,Podolsky D,Dreisow F,Nolte S,Segev M,Szameit A 2013Nature496 196

[43]Hafezi M,Demler E A,Lukin M D,Taylor J M 2011Nat.Phys.7907

[44]Hafezi M,Mittal S,Fan J,Migdall A,Taylor J M 2013Nat.Photon.71001

[45]Liang G Q,Chong Y D 2013Phys.Rev.Lett.110 203904

[46]Petrescu A,Houck A A,Le Hur K 2012Phys.Rev.A86 053804

[47]Rechtsman M C,Zeuner J M,Tunnermann A,Nolte S,Segev M,Szameit A 2013Nat.Photon.7153

[48]Wang Y H,Steinberg H,Jarillo-Herrero P,Gedik N 2013Science342 453

[49]Guzmán-Silva D,Mejía-Cortés C,Bandres M A,Rechtsman M C,Weimann S,Nolte S,Segev M,Szameit A,Vicencio R A 2014New J.Phys.16 063061

[50]Lin Q,Fan S 2014Phys.Rev.X4 031031

[51]Mittal S,Fan J,Faez S,Migdall A,Taylor J M,Hafezi M 2014Phys.Rev.Lett.113 087403

[52]Ozawa T,Carusotto I 2014Phys.Rev.Lett.112 133902

[53]Terças H,Flayac H,Solnyshkov D D,Malpuech G 2014Phys.Rev.Lett.112 066402

[54]Tzuang L D,Fang K,Nussenzveig P,Fan S,Lipson M 2014Nat.Photon.8 701

[55]Hu W,Pillay J C,Wu K,Pasek M,Shum P P,Chong Y D 2015Phys.Rev.X5 011012

[56]Schmidt M,Kessler S,Peano V,Painter O,Marquardt F 2015Optica2 635

[57]Gao F,Gao Z,Shi X,Yang Z,Lin X,Xu H,Joannopoulos J D,Soljacic M,Chen H,Lu L,Chong Y,Zhang B 2016Nat.Commun.711619

[58]Fleury R,Khanikaev A B,Alù A 2016Nat.Commun.7 11744

[59]He C,Li Z,Ni X,Sun X C,Yu S Y,Lu M H,Liu X P,Chen Y F 2016Appl.Phys.Lett.108 031904

[60]Peng Y G,Qin C Z,Zhao D G,Shen Y X,Xu X Y,Bao M,Jia H,Zhu X F 2016Nat.Commun.7 13368

[61]Harper P G 1955Proc.Phys.Soci.Sec.A68 874

[62]Aubry S,André G 1980Ann.Israel Phys.Soc.3 18

[63]Kohmoto M,Kadano ffL P,Tang C 1983Phys.Rev.Lett.50 1870

[64]Kraus Y E,Lahini Y,Ringel Z,Verbin M,Zilberberg O 2012Phys.Rev.Lett.109 106402

[65]Verbin M,Zilberberg O,Kraus Y E,Lahini Y,Silberberg Y 2013Phys.Rev.Lett.110 076403

[66]Zak J 1989Phys.Rev.Lett.62 2747

[67]Su W P,Schrie ff er J R,Heeger A J 1979Phys.Rev.Lett.42 1698

[68]Xiao M,Zhang Z Q,Chan C T 2014Phys.Rev.X4 021017

[69]Xiao M,Ma G,Yang Z,Sheng P,Zhang Z Q,Chan C T 2015Nat.Phys.11 240

[70]Kitaev A Y 2001Physics-Uspekhi44 131

[71]PoddubnyA,MiroshnichenkoA,SlobozhanyukA,Kivshar Y 2014ACS Photon.1 101

[72]Lu L,Fang C,Fu L,Johnson S G,Joannopoulos J D,Soljacic M 2016Nat.Phys.12 337

[73]Wang H,Xu L,Chen H,Jiang J H 2016Phys.Rev.B93 235155

[74]Lu L,Fu L,Joannopoulos J D,Soljacic M 2013Nat.Photon.7294

[75]Lu L,Wang Z,Ye D,Ran L,Fu L,Joannopoulos J D,Soljačić M 2015Science349 622

[76]Xiao M,Chen WJ,He W Y,Chan C T 2015Nat.Phys.11 920

[77]Yang Z,Zhang B 2016Phys.Rev.Lett.117 224301

[78]Noh J,Huang S,Leykam D,Chong Y D,Chen K P,Rechtsman M C 2017Nat.Phys.13 611

PACS:42.70.Qs,03.65.VfDOI:10.7498/aps.66.224203

*Project supported by the National Key Ramp;D Program of China(Grant No.2017YFA0303702),the National Natural Science Foundation of China(Grant Nos.11134006,11474158,11404164,11625418),the Natural Science Foundation of Jiangsu Province,China(Grant No.BK20140019),and the support from Academic Program Development of Jiangsu Higher Education(Grant No.PAPD).

†Corresponding author.E-mail:luminghui@nju.edu.cn

Topological properties of arti ficial bandgap materials∗

Sun Xiao-Chen1)He Cheng1)2)Lu Ming-Hui1)2)†Chen Yan-Feng1)2)

1)(National Laboratory of Solid State Microstructures,Department of Materials Science and Engineering,Nanjing University,Nanjing 210093,China)2)(Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China)

20 September 2017;revised manuscript

6 November 2017)

Recently,arti ficial bandgap materials(such as photonic crystals and phononic crystals)have been becoming the research hotspot of the next generation intelligent materials,because of its extremely designable,tunable and controllable capacity of classical waves.On the other hand,topological material phase,originally proposed and first demonstrated in Fermionic electronic systems,has been proposed in more and more Bosonic systems.In this review paper,we first focus on some of the representative photonic/phononic topological models,and four common types of topological photonic system are discussed:1)photonic/phononic quantum Hall e ff ect with broken time-reversal symmetry;2)photonic topological insulator and the associated pseudo-time-reversal symmetry protected mechanism;3)time/space periodically modulated photonic Floquet topological insulator;4)a summary and outlook including a brief introduction of Zak phase in onedimensional systems and Weyl point in three-dimensional systems.Finally,the underlying Dirac model is analyzed.

arti ficial bandgap material,topology,Dirac equation

10.7498/aps.66.224203

∗国家重点研发计划(批准号:2017YFA0303702)、国家自然科学基金(批准号:11134006,11474158,11404164)、国家自然科学基金杰出青年基金(批准号:11625418)、江苏省自然科学基金(批准号:BK20140019)和江苏高校优势学科建设工程项目(批准号:PAPD)资助的课题.

†通信作者.E-mail:luminghui@nju.edu.cn