基于高维随机矩阵的系统状态评估方法研究
程含渺, 李红斌, 徐 晴, 纪 峰, 陈 刚 , 田正其
(1. 国家电网公司电能计量重点实验室(国网江苏省电力有限公司电力科学研究院), 江苏 南京 210019;2. 华中科技大学电气与电子工程学院,湖北 武汉 430074)
0 引言
元素为随机变量的矩阵称为随机矩阵,最初源于数理统计研究,经过数十年发展,随机矩阵理论逐步完善。20世纪50年代,物理学家Wigner证明了半圆律[1-2]。1976年,马尔琴科和帕斯图证明了马尔琴科-帕斯图(M-P)定理[3]。目前,随机矩阵理论已应用于核物理、多元统计、无线电通信、经济学、生物学等领域[4-10]。近两年,电力数据分析引入了大数据方法[11-15],高维随机矩阵作为一种处理工具,也开始崭露头角。
文献[16]首次用高维随机矩阵对电网运行数据进行建模分析。文献[17—18]在此基础上,着重研究了高维随机矩阵在负荷关联分析的应用。文献[19]研究了高维随机矩阵在广域量测数据异常检验方面的应用。文献[20]研究了使用高维随机矩阵方法评估变压器运行健康状态,并将其与传统方法进行了比较。
虽然高维随机矩阵理论在状态评估方面的研究文献较多,但在基础性方面还不完善:(1) 没有描述高维随机矩阵的适用性;(2) 评估判据指标只有平均谱半径(mean spectral radius,MSR);(3) 数据处理步骤复杂。文中在现有研究成果的基础上,提炼了高维随机矩阵的应用条件,阐述了应用方法,提出了另2个状态评估指标量,讨论了单环定理的编程步骤,以电力设备健康状态评估和电网运行状态评估为例进行了应用仿真。
1 高维随机矩阵数学基础
高维随机矩阵理论属于多元统计学研究领域,极限谱分布是其重要研究内容,以下介绍与状态评估密切相关的2个重要谱分布[21-24]。
1.1 马尔琴科-帕斯图定理
令随机矩阵X=(xij)n×m,矩阵X任意列中的元素xkj(k=i,j=1,2,…)是均值为0,方差为σ2的独立同分布随机变量,则矩阵X的样本协方差矩阵定义为:
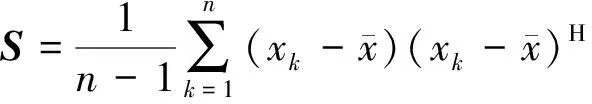
(1)
式中:xk为矩阵Xn的第k列。在一般情况下,矩阵Xn的样本协方差也可以简单定义为:
(2)
式中:Sn为Wishart矩阵。当m/n→c∈(0,∞),Sn的极限谱分布依概率收敛到概率密度函数为式(3)的谱分布函数,简称为M-P律,且当σ2=1时,称为标准M-P律。
(3)
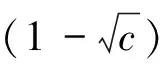
1.2 单环定理
假设随机矩阵A=(xij)n×n可以分解为A=PTQ,其中P和Q为n阶Haar酉矩阵,T是对角阵,对角线元素是A的奇异值。当满足一定的条件时,矩阵A的极限谱分布由其奇异值的概率测度唯一确定,且特征值在复平面上收敛到圆环,圆环的内外半径分别为:
(4)
式中:v为矩阵A的奇异值的概率测度。在实际应用中,考虑矩阵A=(xij)∈Cp×N为非-Hermitian矩阵,其元素为独立同分布的随机变量,且矩阵A的列向量满足均值为0、方差为1。对于L个矩阵Ai,定义矩阵乘积Z为:
(5)
式中:Au,i为Ai的奇异值等价矩阵。将矩阵Z标准化为Zstd,使其满足σ2(zi)=1/N,则Zstd的极限谱分布依概率收敛到概率密度函数为式(6)的谱分布函数。
(6)
式中:λz为特征值;d为p/N∈{(0,1],p,N→∞}。Zstd的特征值在复平面的分布是一个圆环,内环半径为(1-d)L/2,外环半径为1。
2 高维随机矩阵应用方法
2.1 适用条件
一般来说,表征系统状态的可测状态参量有N个,假设分别为{P1,P2,…,PN},可测是指可以直接或间接测量。现对可测状态参量Pi(i=1,2,…,N)与系统状态的关系作如下3个一般性假设。
(1) 理想状态下,N个可测状态参量保持基本恒定不变,仅在均值水平附近正态随机波动,且这种随机波动过程是平稳的,则第i个状态参量在任意时刻的测量值pim为:
pim=μ(pi)+εi
(7)
式中:μ(pi)为第i个可测状态参量的均值水平;εi为第i个可测状态参量的随机波动量;波动量应满足μ(εi)=0,σ2(εi)=const(const为常量)。
(2) 若第i个可测状态参量的测量值出现异常波动,不再是平稳正态随机波动,即μ(εi)≠0或σ2(εi)≠const,则怀疑该系统的状态存在变化。
(3) 若有多个可测状态参量出现(2)所描述的情况,则有更加充分的理由怀疑系统状态发生了变化。
需要说明的是,当应用条件不满足上述基本假设条件时,可以对可测量进行适当变换。例如,在文献[19]中,对变压器各状态参量的测量数据用AR(1)、ARMA(1,1)等低阶模型拟合,再求残差序列,用残差值构建高维随机矩阵。
2.2 高维矩阵构建方法
假设在状态评估时间窗内,对系统的K个可测状态参量测量T次,则在截取的时间窗内,所有测量数据可以构成K行T列矩阵:
(8)
式中:矩阵D的元素xij表示第i个可测状态参量在j时刻的测量值。当K和T充分大,并且K和T是同一数量级时,矩阵D是一个高维随机矩阵。对矩阵D进行标准化,使标准化之后的矩阵Dstd=(yij)K×T满足:
(9)
式中:yi=(yi1,yi2,…,yiT),1≤i≤K,则矩阵Dstd一般为非-Hermitian矩阵。当K,T→∞且K/T→c时,矩阵Dstd满足如下性质:(1) 样本协方差矩阵的极限谱分布满足标准M-P律;(2) 奇异值等价矩阵通过Haar酉矩阵变换得到的标准化乘积矩阵应满足标准单环定理。
可以通过检验Dstd是否满足上述性质来评估设备或系统的可测状态参量是否发生异常波动。为了检验Dstd是否偏离上述性质,需要选择合适的统计量作为评估判据指标。
2.3 评估判据指标
2.3.1 谱分布概率密度函数相似度判据
假设正常状态时,由状态量测量值构成的随机矩阵的样本协方差矩阵为S1,S1的特征值分布概率密度函数为f1(x)。当状态发生变化时,其状态量测量值构成的随机矩阵的样本协方差矩阵为S2,S2的特征值分布概率密度函数为f2(x)。显然,状态变化前后的S1和S2有差异,对应的f1(x)和f2(x)也会有差异。因此,可以将f1(x)和f2(x)的差异程度作为状态变化的定量评估判据指标。
设有2个概率密度函数f1(x),x∈[b1,h1]和f2(x),x∈[b2,h2],定义概率密度函数的差异程度υ为:
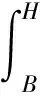
(10)
式中:B=min(b1,b2),H=min(h1,h2)。υ越小表示2个概率密度函数的差异越小。在实际应用中,可以将f1(x)和f2(x)分别与标准M-P律求差异度,再比较两个差异度的大小。
2.3.2 特征值线性统计量判据
正常状态下,服从单环定理的特征值会均匀分布在圆环内,若状态发生异常变化,特征值分布会随之变化,分布不再均匀,导致圆环的形态改变。因此,可以使用特征值的分布环半径以及分布集中程度作为状态是否变化的评估判据指标,通常用矩统计量表征。
假设随机变量的一个样本为X={X1,X2,…,Xn},则该样本的k阶中心矩αk为:
(11)
式中:E(X)为样本期望。同理,可以定义样本的k阶原点矩βk为:
(12)
对于随机矩阵的n阶样本协方差矩阵Sn×n,若Sn×n的特征值为λ={λ1,λ2,…,λn},其一阶原点矩的物理意义是平均谱半径,二阶中心矩的物理意义是特征值距离平均谱半径的距离平方和。因为特征值分布越集中,平均谱半径越大,所以可以采用一阶原点矩β1和二阶中心矩α2作为状态评估判据指标。
3 单环定理编程步骤
单环定理编程步骤实际上也是高维测量数据的处理方法,文献[16—20]已经进行了具体阐述,但过程复杂。文中在上述文献的研究基础上,对编程步骤作了进一步讨论。
依照单环定理的描述,在获得原始数据矩阵X之后,应求取矩阵T,具有以下性质[23-24]:(1) 是一个对角矩阵;(2) 对角线元素是矩阵A的奇异值;(3) 矩阵A是将T用2个Haar酉矩阵进行变换得到。根据单环定理的描述,在使用数学工具如Matlab编程时,具体步骤如下:
(1) 将n个变量的测量数据xi(ti)按照时间顺序排列,再分段截取构成待处理的原始高维矩阵X;
(2) 用奇异值分解函数对原始矩阵X作奇异值分解,得到对角矩阵Xsng,该过程不依赖Haar酉矩阵;
(3) 生成2个标准Haar酉矩阵U和V,按照式(13)将Xsng变换为矩阵Zorg:
Zorg=UXsngV
(13)
(4) 将矩阵Zorg按照式(9)标准化得到Zstd,最后再求Zstd的特征值。
依照上述4个步骤,Zstd的特征值分布呈标准的单环。关于Haar酉矩阵的生成方法,可以参看文献[25],矩阵Zorg的标准化方法可以参看文献[16—20],在运算过程中,还要注意矩阵的行列数符合矩阵运算条件。
4 电力设备健康状态评估
电力设备健康状态往往由多个参量共同决定,变压器的状态参量包括油中溶解气体、绝缘电阻、介质损耗、油中微水等,断路器状态参量包括触头电磨损、分合闸线圈电流、开断行程等。将这些状态量的测量值,构建成高维随机矩阵,则可以通过分析矩阵性质评估电力设备健康状态。
假设某电力设备的可测状态参量有3个,记为P1,P2,P3。在正常状态下,这3个可测状态量在其均值附近随机波动。在某一时刻,由于状态发生恶化,导致状态量P3出现异常(或者可测状态量P3出现异常,导致状态恶化)。3个状态参量的测量数据曲线如图1所示。
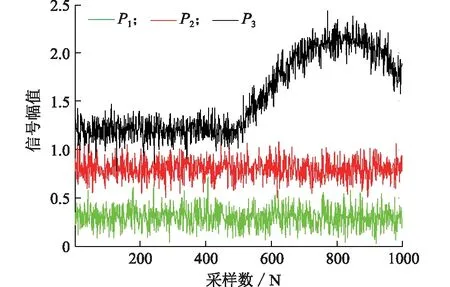
图1 设备可测状态参量的数据曲线Fig.1 Measured parameter data curve of equipment
图中:信号幅值单位为1,采样数据一共为1000组,假设在第500组采样点处状态量P3发生异常波动,持续时间为500组采样点。
4.1 第一组数据仿真
数据取自图1中的1—500组采样点,得到一个3×500矩阵,采用文献[21]的矩阵扩充方法将矩阵扩充为300×500矩阵。根据M-P律和单环定理实施方法,得到的仿真结果如图2所示。

图2 第一组仿真结果Fig.2 The first simulation results
4.2 第二组数据仿真
数据取自图1中的501—1000组采样点,参照第一组仿真过程,得到的仿真结果如图3所示。
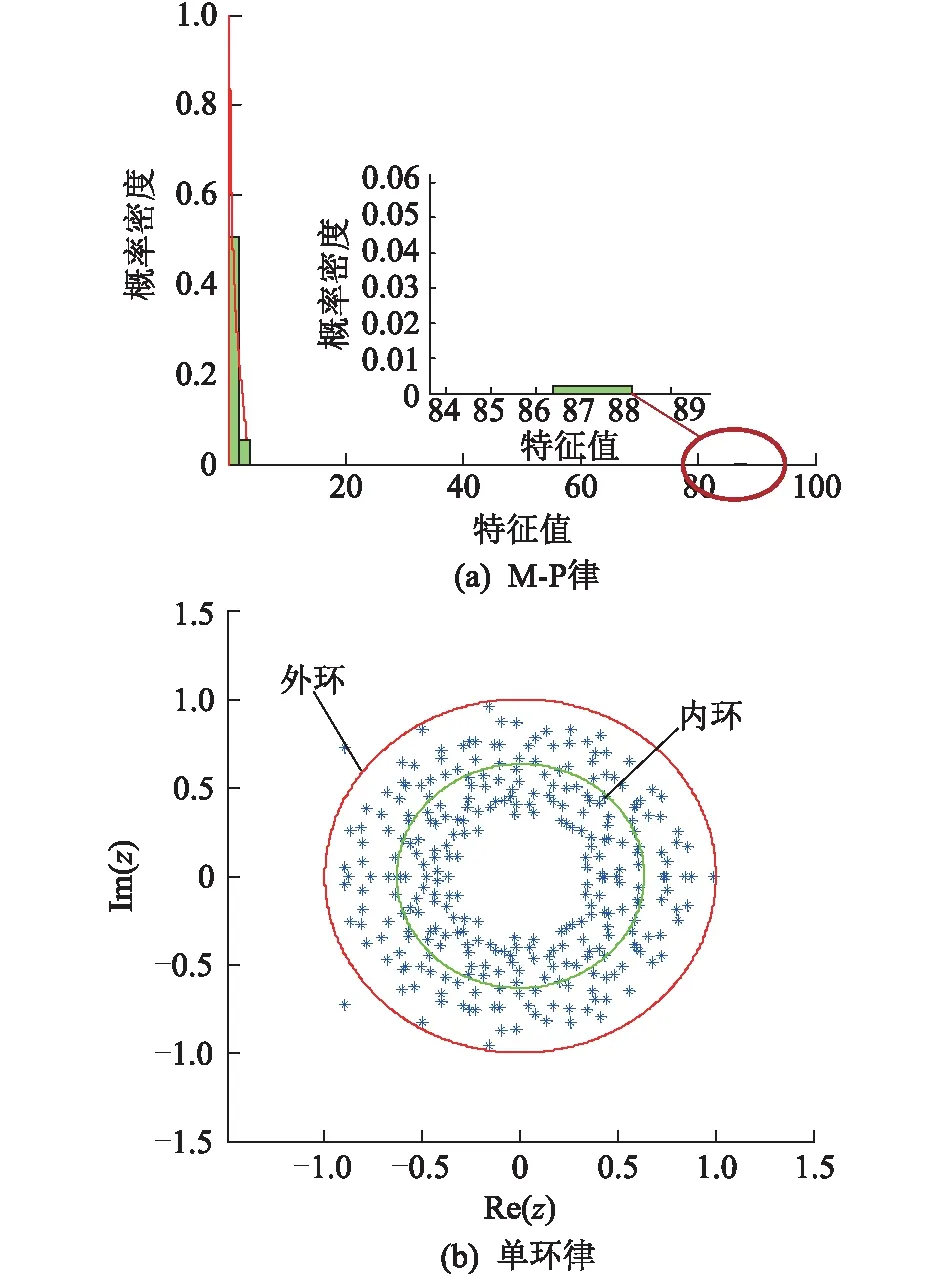
图3 第二组仿真结果Fig.3 The second simulation results
从2组仿真结果可以看出,第一组与第二组的仿真结果有明显差异,具体表现在:(1) 第二组仿真结果出现了重大特征值,偏离M-P律的程度变大;(2) 第二组仿真结果中特征值超出圆环内径,环内的特征值分布更分散。若将2.3.1中的3个定量评估判据指标记为J1,J2,J3,分别计算两组仿真结果的判据量化值,结果如表1所示。
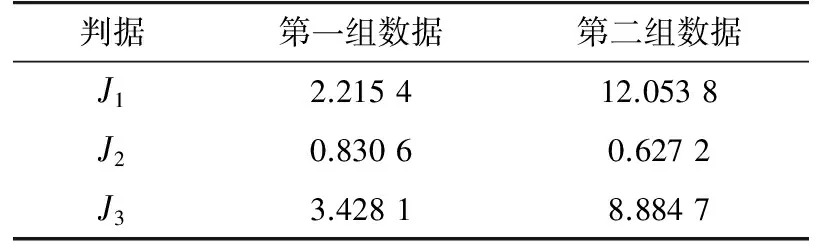
表1 评估判据指标计算结果Tab.1 The calculation results of evaluation criterion
从表1可以看出,当设备或系统的可测状态量数据出现异常时,判据量化值具有显著变化。第二组数据的仿真结果与第一组相比:(1)J1变大,说明第二组数据偏离M-P律的程度变大;(2)J2变小,说明第二组数据的单环平均半径变小,特征值向中心分散;(3)J3变大,环内的特征值分布更分散。在实际应用时,适当选择滑动时间窗,实时计算3个评估判据指标,得到3条指标曲线,则可以根据曲线的波动情况对设备状态进行评估。
5 电网运行状态评估
评估电网运行状态一般需要依赖电网拓扑结构,但随着电网规模越来越大,拓扑结构变得越来越复杂,建模分析难度也随之增大。可以对电网节点电压数据构建高维矩阵,通过分析矩阵性质从而评估电网运行状态,从而实现依赖于电网拓扑结构的状态评估,文献[26]也进行了类似探索研究。采用Power System Toolbox(PST)仿真工具,针对图4所示的新英格兰10机39节点典型电力系统,对基于高维随机矩阵理论的电网运行异常状态评估方法进行了仿真验证。仿真时间步进设置为0.01 s,仿真时长设置为2 s,假设在第1.8 s时,线路3-4发生对地三相短路故障,随后故障恢复,1.85 s时清除近端故障告警,1.9 s时清除远端故障告警,相关断路器先后合闸,母线节点电压仿真结果如图5所示。
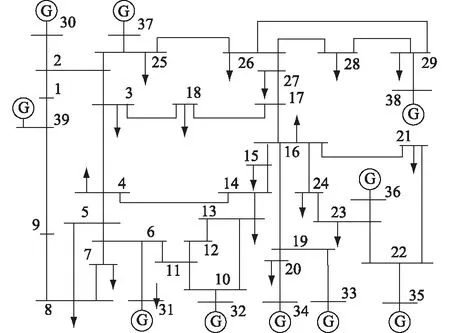
图4 新英格兰10机39节点系统Fig.4 The New-England 10-generator 39-bus system
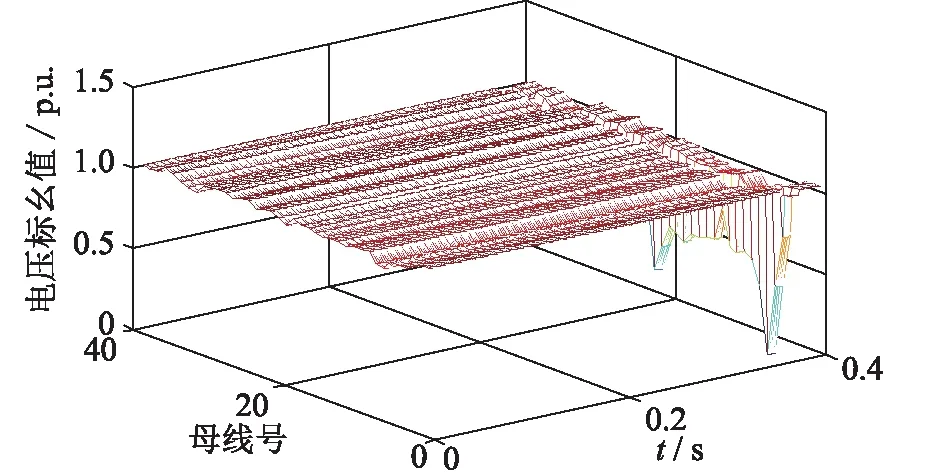
图5 节点电压仿真结果Fig.5 Simulation result of bus voltage
由图5可知,在1.85 s故障发生时,各母线电压出现了不同程度跌落,3号母线电压跌落至零,距离3号母线越远,电压跌落程度越小。用高维随机矩阵的方法识别本次故障,第一组数据取第1 s内的运行结果,第二组数据取第2 s内的运行结果。参照式(8),构建39行100列的矩阵,计算结果如图6所示,定量评估判据指标计算结果如表2所示。
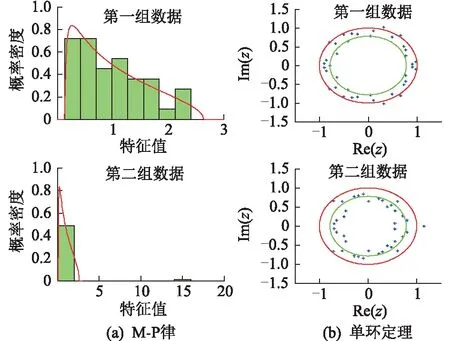
图6 高维随机矩阵处理所得结果Fig.6 Results obtained after handling with large dimensional random matrices
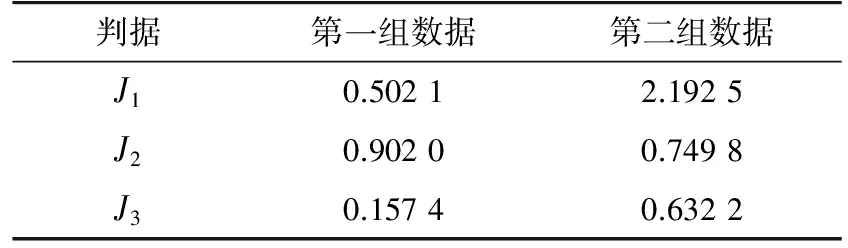
表2 评估判据指标计算结果Tab.2 The calculation results of evaluation criterion
从仿真结果可以看出,与应用于电力设备状态评估的结果类似,当电网发生故障时,矩阵谱分布偏离M-P律和单环律,与电网正常状态时的计算结果相比,有明显差异。对于图6中的第二组数据计算结果而言,图6(a)在15处出现异常特征值,图6(b)的特征值分布超出圆环范围。
6 结语
文中提炼了高维随机矩阵应用条件,即在系统正常稳定时,其表征系统状态的可测参量本身或经处理后是平稳随机变量。总结了高维随机矩阵应用方法,着重讨论了单环定理实现步骤,其关键是第2步和第3步。列举了两个应用实例,仿真结果表明,应用高维随机矩阵的方法,可以识别设备或系统状态变化。本文对将高维随机矩阵应用于评估系统状态的研究者具有参考价值。
[1] WIGNER E P. Characteristic vectors of bordered matrices with infinite dimensions [J]. Annals of Mathematics, 1955, 62(3): 548-564.
[2] WIGNER E P. On the distribution of the roots of certain symmetric matrices [J]. Annals of Mathematics, 1958, 67(2): 325-327.
[3] MARCHENKO V, PASTUR L. Distributions of eigenvalues for some sets of random matrices [J]. Mathematics of the USSR-Sbornik, 1967(1): 457-483.
[4] FEINBERG J, ZEE A. Non-hermitian random matrix theory: method of hermitian reduction[J]. Nuclear Physics B, 1997,504(3): 579-608.
[5] 姜丹丹, 白志东. 大维随机矩阵谱理论在多元统计分析中的应用[M]. 北京:知识产权出版社,2014.
JIANG Dandan,BAI Zhidong. Application of large dimensional random matrix spectral theory in multivariate statistical analysis[M]. Beijing: Intellectual Property Press,2014.
[6] JOSEPH A, GUO T, QIU R C. Visualization of large wireless network behavior using random matrix theory [C]∥In Proceedings of 2015 IEEE Wireless Communications and Networking Conference. 2015: 2097-2102.
[7] 白志东, 方兆本, 梁应敞. 高维随机矩阵的谱理论及其在无线通信和金融统计中的应用[M]. 合肥: 中国科学技术大学出版社, 2009.
BAI Zhidong,FANG Zhaoben,LIANG Yingchang. Spectral theory of high dimensional random matrices and its applications in wireless communication and financial statistics[M]. Hefei:China University of Science and Technology Press,2009.
[8] 韩 华, 吴翎燕, 宋宁宁. 基于随机矩阵的金融网络模型[J]. 物理学报,2014,63(13):431-440.
HAN Hua, WU Lingyan, SONG Ningning. Financial networks model based on random matrix [J]. Acta Physica Sinica, 2014, 63(13):431-440.
[9] PLEROU V, GOPIKRISHNAN P, ROSENOW B, et al. A random matrix approach to cross-correlations in financial data [J]. Physical Review E, 2002, 65: 1-19.
[10] 李 蓉, 颜平兰, 陈 健, 等. 随机矩阵理论在肺癌基因网络识别中的应用[J]. 物理学报,2009,58(10):6703-6708.
LI Rong, YAN Pinglan, CHEN Jian, et al. Application of random matrix theory to identification of lung cancer gene networks [J]. Acta Physica Sinica, 2009,58(10):6703-6708 .
[11] 许海清, 黄 敏. 浅谈电力大数据对信息运行的影响[J]. 江苏电机工程, 2015,34(2):62-64.
XU Haiqing, HUANG Min. A discussion on the influence of power big data on information operation [J]. Jiangsu Electrical Engineering, 2015,34(2):62-64.
[12] 张友强,寇凌峰,盛万兴,等. 配电变压器运行状态评估的大数据分析方法[J]. 电网技术, 2016, 40(3):768-773.
ZHANG Youqiang, KOU Lingfeng, SHENG Wanxing, et al. Big data analytical method for operating state assessment of distribution transformer [J]. Power System Technology, 2016, 40(3):768-773.
[13] 李 刚,刘 燕,宋 雨,等. 基于信息融合的电力大数据可视化预处理方法[J]. 广东电力,2016,29(12):10-14.
LI Gang, LIU Yan, SONG Yu, et al. Visualization pretreatment method for electric power big data based on information fusion[J]. Guangdong Electric Power,2016,29(12):10-14.
[14] 张 魁,王亚明,刘 明,等. 基于大数据及智能算法的连云港电量负荷预测研究[J]. 江苏电机工程, 2016,35(3):49-52.
ZHANG Kui, WANG Yaming, LIU Ming, et al. Research on electricity consumption and load prediction of Lianyungang based on big data and intelligent algorithm [J]. Jiangsu Electrical Engineering, 2016,35(3):49-52.
[15] 郑海雁,金 农,季 聪,等. 电力用户用电数据分析技术及典型场景应用[J]. 电网技术,2015,39(11):3147-3152.
ZHENG Haiyan,JIN Nong,JI Cong,et al. Analysis technology and typical scenario application of electricity big data of power consumers [J]. Power System Technology,2015,39(11):3147-3152.
[16] HE X, AI Q, QIU R C , et al. A big data architecture design for smart grids based on random matrix theory [J]. IEEE Transactions on Smart Grid, 2017,8(2):674-686.
[17] XU X , HE X,AI Q, et al. A correlation analysis method for power systems based on random matrix theory [J]. IEEE Transactions on Smart Grid, 2015(99):1-10.
[18] 徐心怡, 贺 兴, 艾 芊, 等. 基于随机矩阵理论的配电网运行状态相关性分析方法[J]. 电网技术, 2016, 40(3): 781-790.
XU Xinyi, HE Xing, AI Qian, et al. A correlation analysis method for operation status of distribution network based on random matrix theory [J]. Power System Technology, 2016, 40(3): 781-790.
[19] 魏大千, 王 波, 刘涤尘, 等. 高维随机矩阵描述下的量测大数据建模与异常数据检测方法[J]. 中国电机工程学报,2015,35(s1):59-66.
WEI Daqian, WANG Bo, LIU Dichen, et al. A method for WAMS big data modeling and abnormal data detection with large random matrices [J]. Proceedings of the CSEE,2015,35(s1.):59-66.
[20] 严英杰, 盛戈皞, 王 辉, 等. 基于高维随机矩阵大数据分析模型的输变电设备关键性能评估方法[J]. 中国电机工程学报, 2015, 36(2): 435-445.
YAN Yingjie, SHENG Gehao, WANG Hui, et al. The key state assessment method of power transmission equipment using big data analyzing model based on large dimensional random matrix [J]. Proceedings of the CSEE,2015, 36(2): 435-445.
[21] 胡 江. 大维随机矩阵经验谱分布函数的收敛[D]. 长春: 东北师范大学, 2012.
HU Jiang. Convergence of empirical spectral distribution function for large dimensional random matrices[D]. Changchun: Northeast Normal University,2012.
[22] 曾杏元. 生成于四种流形上的大维随机矩阵的谱分布[D]. 南京:中南大学, 2013.
ZENG Xinyuan. Spectral distribution of large dimensional random matrices generated on four manifolds[D]. Nanjing: Central South University,2013.
[23] GUIONNET A, KRISHNAPUR M, ZEITOUNI O. The single ring theorem [J]. Annals of Mathematics, 2011, 174(2): 1189-1217.
[24] FEINBERG J, SCALETTAR R, ZEE A. “Single ring theorem” and the disk-annulus phase transition [J]. Journal of Mathematical Physics, 2001, 42(12): 5718-5740.
[25] PETZ D, REFFY J. On asymptotics of large Haar distributed unitary matrices [J]. Periodica Mathematica Hungarica,2004,49(1):103-117.
[26] HE X, QIU R C , AI Q,et al. Designing for situation awareness of future power grids: an indicator system based on linear eigenvalue statistics of large random matrices [EB/OL]. IEEE Transactions on Smart Grid, 2016, DOI: 10.1109/ACCESS.2016.2581838.

