聚焦圆中角的应用

文/翟士波

在圆中，圆心角与圆周角是最常见的角.它们与弦、弧和扇形的联系比较密切，是中考命题的重点.下面举例说明圆中角的各种应用.

一、求角的大小

1.利用圆心角求圆周角

例1 如图1，△ABC内接于⊙O，且OB⊥OC，则∠A的度数是（ ）

A．90°. B．50°. C．45°. D．30°.

温馨小提示：在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半．

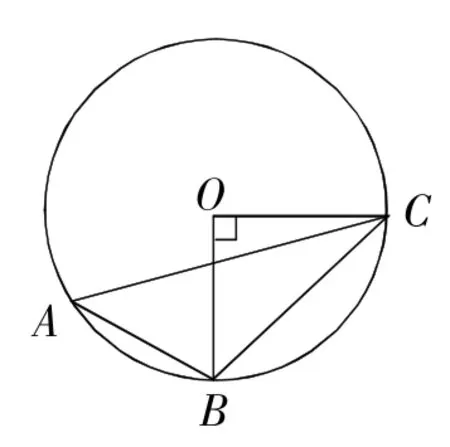
图1

2.利用圆周角求圆心角

例 2 如图2，点A，B，C在⊙O上，AC∥OB，∠BAO=25°，则∠BOC的度数为（ ）

A．25°. B．50°. C．60°. D．80°.

解：∵OA=OB，∠BAO=25°，∴∠B=25°．

∵AC∥OB，∴∠CAB=∠B=25°，

∴∠BOC=2∠CAB=50°．选B．

温馨小提示：在圆中，常用到圆的半径相等构造等腰三角形解题．

图2

3.利用直径所对的圆周角是直角求角

例 3 如图3，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED=20°，则∠BCD的度数为（ ）

A．100°. B．110°. C．115°. D．120°.

解：连接AC.

∵AB为⊙O的直径，∴∠ACB=90°，

∵∠AED=20°，∴∠ACD=20°，

∴∠BCD=∠ACB+∠ACD=110°. 选B．

温馨小提示：当有直径时，通常会添加辅助线，利用直径所对的圆周角是直角解题．

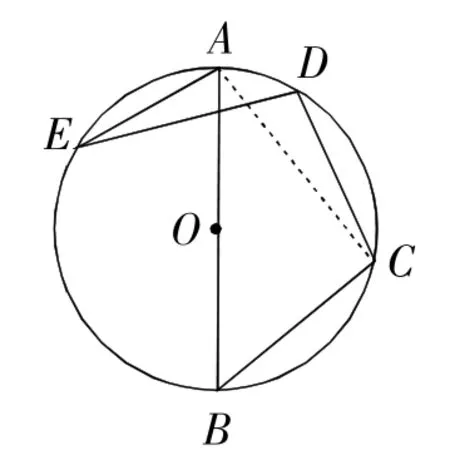
图3

4.利用圆内接四边形对角互补求角

例4 如图4，A，B，C是⊙O上的三点，且四边形OABC是菱形.若点D是圆上异于A，B，C的另一点，则∠ADC的度数是______．

解：连接OB.

∵四边形OABC是菱形，∴AB=OA=OB=BC，

∴△AOB是等边三角形，即∠AOB=60°，∴∠AOC=120°，

∴∠ABC=∠AOC=120°.

答案为：60°或120°．

温馨小提示：已知圆上的三点，当第四个点的位置不确定时，要画出图形,利用圆的相关定理求解．

图4

5.利用圆心角、圆周角求其他角

例5如图5，AB是⊙O的直径，直线DA与⊙O相切于点A，DO交⊙O于点C，连接BC，若∠ABC=21°，则∠ADC的度数为（ ）

A．46°. B．47°. C．48°. D．49°.

解：∵OB=OC，∴∠BCO=∠B=21°，

∴∠AOD=∠B+∠BCO=21°+21°=42°，

∵AB是⊙O的直径，直线DA与⊙O相切于点A，

∴∠OAD=90°，∴∠ADC=90°-∠AOD=90°-42°=48°．

选C．

温馨小提示：出现切线时，通常连接圆心和切点,构造直角三角形求解．

图5

二、求弦长

例 6 如图6，△ABC内接于⊙O，∠ACB=90°，∠ACB的角平分线交⊙O于D.若AC=6，则BC的长为_____．

解：连接AD.

∵∠ACB=90°，∴AB是⊙O的直径.

∵∠ACB的角平分线交⊙O于D，

∴∠ACD=∠BCD=45°，∴∠DAB=∠DBA=45°，

∵AB是⊙O的直径，∴△ABD是等腰直角三角形，

温馨小提示：求弦长，一般需要构造直角三角形，转化为求直角三角形的边的问题．

图6

三、求弧长

例 7 如图7，▱ABCD中，∠B=70°，BC=6，以AD为直径的⊙O交CD于点E，则的长为（）

解：连接OE.

∵四边形ABCD是平行四边形，

∴∠D=∠B=70°，AD=BC=6，∴OA=OD=3，

∵OD=OE，∴∠OED=∠D=70°，∴∠DOE=180°-2×70°=40°，

温馨小提示：熟练掌握平行四边形的性质，求出∠DOE的度数是解题的关键．

图7

四、求面积

例8 如图8，在△ABC中，AB=AC，∠ABC=45°，以AB为直径的⊙O交BC于点D，若则图中阴影部分的面积为（ ）

A.π+1. B.π+2. C.2π+2. D.4π+1.

解：连接OD,AD.

在△ABC中，AB=AC，∠ABC=45°，

∴∠C=45°，∴∠BAC=90°，

∵AB为直径，∴∠ADB=90°，BO=DO=2，

∵OD=OB，∠B=45°，∴∠B=∠BDO=45°，∴∠DOA=∠BOD=90°，

温馨小提示：把阴影部分拆分成扇形DOA和△DOB是解此题的关键．

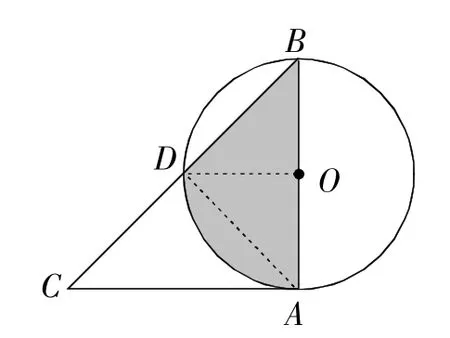
图8