高维厚尾金融数据协方差阵的统计估计及应用
刘丽萍(贵州财经大学 数学与统计学院,贵州 贵阳 550025)
一、引 言
在大数据时代,随着数据可获得性的提高,金融数据的维度呈爆炸式增长。目前,国外已有不少学者在变量选择方面对高维数据进行了研究[1-2],但国内对于如何估计高维资产协方差阵的研究并不多见,协方差阵在投资组合和风险管理中扮演着重要角色,如何估计高维金融数据的协方差阵已是统计领域中越来越重要的亟待解决的问题。近年来,已有很多学者对高维协方差阵的估计问题进行了研究;Fan等不仅提出了基于因子结构的协方差阵估计方法,还提出了基于主成分分析的高维协方差阵估计方法[3-4];Cai和Zhou、Cai和Liu提出了基于门限函数的稀疏协方差阵估计方法[5-6];Wu和Pourahmadi[7]、Li和Wang等[8]将乔列斯基分解法和非参数收缩法相结合,提出了基于乔列斯基分解的高维协方差阵估计方法;还有学者提出了高维数据的动态协方差阵估计方法。
上述方法都是在数据服从正态分布的假定下进行的。但是,金融数据大多是服从厚尾分布的,极端风险出现的次数要明显多于正态分布,而考虑金融数据的厚尾特征,有助于发现市场的异常走向,防范和化解金融极端风险。在估计金融数据的协方差阵时,通常采用的惩罚最小二乘估计法不再适用,因其对误差的分布非常敏感,尤其对于超高维变量而言,由于忽略厚尾分布而产生的噪声大大影响了协方差阵的估计效果,进而会影响投资者的投资决策。
在厚尾分布的假定下,如何估计高维协方差阵的研究还非常少。Xue和Zou针对厚尾数据,提出了基于秩方法的高维协方差阵的估计方法[9],但是该方法的应用并不广泛,因其是在变量之间具有自然顺序的假定下进行的,针对其研究的不足,本文考虑将Fan、Li、Wang提出的RA-Lasso方法和乔列斯基分解法相结合,提出新的方法以估计高维厚尾金融数据的协方差阵(记为ΣRA-Lasso):首先,通过乔列斯基分解法将复杂的高维协方差阵估计方法转化为一系列的回归模型;然后,将基于惩罚Huber损失函数的稳健Lasso方法(RA-Lasso)应用到这一系列的回归模型中,并将一些回归系数压缩为0来精简模型,以达到降维的目的。Fan、Li、Wang的研究指出:RA-Lasso方法能够很好地估计高维厚尾数据的回归模型[10]。因此,笔者将RA-Lasso方法应用到基于乔列斯基分解的回归模型中,在解决维数诅咒问题的同时,很好地克服了金融数据的厚尾特征对协方差阵估计的影响,明显提高了高维协方差阵的估计效率。
二、高维厚尾数据协方差阵的估计
(一)基于乔列斯基分解法的高维协方差阵估计
Wu等提出将乔列斯基分解方法应用到高维协方差阵的估计中,将繁琐的协方差阵估计问题转化为一系列回归模型的估计问题。对于协方差阵Σ,其改进的乔列斯基分解形式如下:
TΣT′=D
(1)
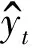
(2)
式(2)也可以写成如下形式:
εt=Tyt
(3)
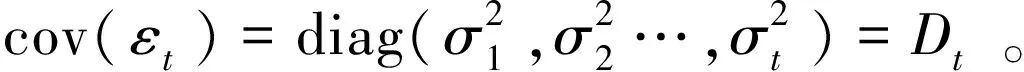
根据式(1)~(3)得协方差阵Σ的估计值为:
(4)
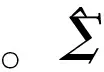
(二)RA-Lasso方法在高维回归模型中的应用
根据Fan、Li、Wang的研究,本文将RA-Lasso方法应用于式(2)所代表的系列回归模型中。在估计式(2)时,首先引入Huber损失函数[11],其形式为:
(5)
Huber损失函数是一种使用鲁棒性回归的损失函数,相比均方误差而言,它对异常值不敏感,对于小的yj值该损失函数是二次的,而对大的yj值该函数则是线性的。根据式(5)知,可将最小二乘回归和最小绝对偏差回归看成是Huber损失函数中α取值为0和的两种极端情况;ια(yj)也被称为近似稳健的二次损失函数,即RA损失函数,其中α为调整参数,是变化的,其取值直接影响到Huber损失函数,而如何选取最优的α值,将在后文详细介绍。
Fan、Li、Wang研究指出:将RA损失函数和Lasso方法相结合得到的RA-Lasso方法,能够解决维数诅咒问题,并很好估计高维数据的回归模型。所以,可将RA-Lasso方法应用到同样是高维回归模型的式(2)中,得到基于RA-Lasso方法的φtj的估计值:
(6)
在式(6)的估计中涉及到两个未知参数α和λ,调整参数α的选择直接影响到Huber损失函数,将采用交叉验证法来选择最优的α。在Wang的研究中指出,惩罚参数λ依赖于样本量n以及资产的维度p,Wang给出λ的取值近似为[12]:
(7)
在后文的研究中,均采用式(7)来计算λ值。
(三)考虑数据厚尾特征的高维协方差阵估计
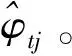
(8)
由式(7)进一步得到:
(9)
从而得到高维厚尾数据协方差阵的估计量ΣRA-Lasso:
(10)
在ΣRA-Lasso估计过程中,先引入乔列斯基分解法将复杂的协方差阵估计问题转化为一系列的回归模型;再在回归模型的估计过程中引入RA-Lasso方法,该方法在解决了维数诅咒的同时,还考虑了由于数据的厚尾特征而引起的估计偏差问题,从而使高维协方差阵的估计更加有效。
三、模拟研究
(一)模拟数据的产生
为了验证ΣRA-Lasso方法的有效性,笔者在模拟研究时采用本文提出的ΣRA-Lasso方法来估计模拟数据的协方差阵,并与其他协方差阵估计方法进行比较以说明其有效性。模拟数据可根据式(11)产生,这是因为本文提出的ΣRA-Lasso方法是将RA-Lasso法直接应用到协方差阵的乔列斯基分解回归模型中的,其形如式(11)的回归模型,即:
(11)
具体的模拟步骤如下:
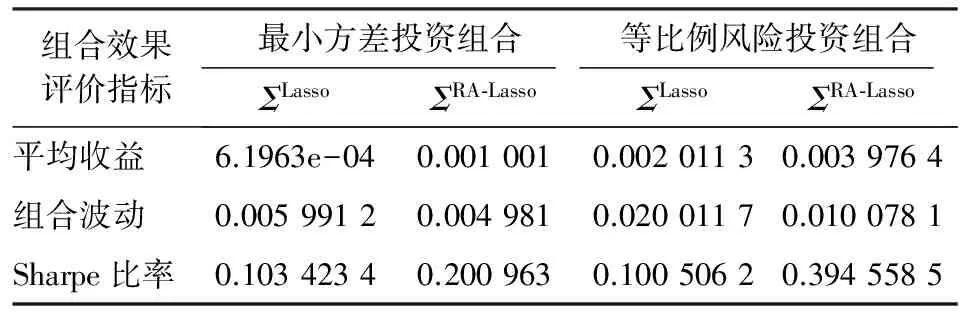
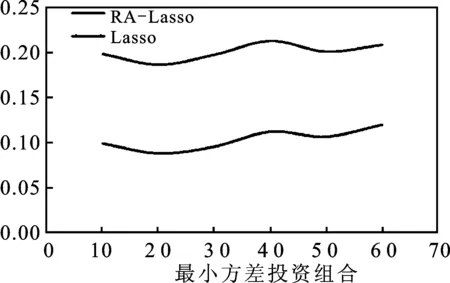
步骤一:令φtj=1-0.3t-j(1≤j 步骤二:对于误差εt分布,考虑两种情况:一种是εt服从于均值为0、方差为2的正态分布;另一种情况是εt服从于自由度为3的t分布。根据εt所属的分布,可以产生n个服从正态分布的残差数据和n个服从t分布的厚尾数据。 步骤三:根据式(11)知y1=ε1,将产生的φtj和εt代入到式(11)中,得到两组数据向量y,y=c(y1,y2,…,yn)′,其中一组为服从t分布的厚尾数据。 步骤四:重复上述步骤N次,便得到了样本量为N、资产维度为n的数据,在本文的研究中取N=200、n=300、n=500。 由式(6)知,在采用ΣRA-Lasso方法估计高维数据的协方差阵时,调整参数α和λ的选择至关重要。将样本量n和资产维度p代入式(7)可得λ。对于参数α,通常采用K折交叉验证法选择最优值。本文选取K=5,即采用5折交叉验证法来选取最优的参数α,即将数据集等分成5份,轮流将其中4份作为训练数据,1份作为测试数据而进行试验;每次试验都会得出相应的正确率,将5次结果的正确率的平均值作为对算法精度的估计。 在本文的研究中,采用的交叉验证的统计量为2-范数损失函数,将其定义为: (12) 图1 最优调整参数α选择图 由图1不难发现,当数据的维度分别为300和500时,通过交叉验证法选择的最优调整参数α的值分别为5.1和5.4。 为了验证ΣRA-Lasso方法的估计效果,将其与Wu和Pourahmadi提出的协方差阵估计方法(ΣLasso)进行比较。ΣLasso方法与本文提出的ΣRA-Lasso方法的思想有些类似,都是在高维协方差阵的估计过程中引入了乔列斯基分解方法,只是ΣLasso方法在估计乔列斯基分解的回归模型时,通过引入Lasso方法来压缩回归系数,以解决维数诅咒问题,而没有考虑到数据的厚尾特征。在比较ΣRA-Lasso和ΣLasso方法时,采用以下两种类型的损失函数作为比较标准: MSE= (13) (14) 本文采用上证180指数成分股进行实证研究,数据来自于CSMAR数据库,样本区间的时间范围为2011年1月4日至2014年9月30日。将交易缺失的数据剔除后所有股票共有交易的天数为906,根据上海证券市场的CSRC行业分类标准,可以将180只股票分成8个板块,分别为:制造业、采掘业、金融保险业、交通运输和仓库业、房地产行业、信息技术业、电气水的生产和供应业以及综合业。由于数据的分布特征会影响到协方差阵的估计效果,所以对全样本股票以及各个板块的收益率数据的分布进行分析。对于样本股票的收益率,本文采用的是对数收益率,即第i只股票在第t日的收益率为Ri,t=log(Pi,t)-log(Pi,(t-1))。股票收益率的正态性分析具体见表2。 表2 股票收益率的正态性分析表 注:用**表示在5%的水平下显著。 从表2可以看出,无论是对于全样本股票还是对于各个板块的股票,其收益率的峰度明显大于3,说明上证股票收益率数据具有明显的尖峰厚尾的特征,并且JB检验在5%的显著水平下均拒绝了正态分布的假定,进一步证实了上证180指数成分股的收益率并不服从正态分布。 1.投资组合的构建。在估计和预测出资产的协方差阵后,将其应用于投资组合。本文主要构建了两种类型的投资组合,即最小方差投资组合和等比例风险投资组合。最小方差投资组合思想是通过寻找组合方差的最小值寻找最优的组合权重向量,当资本市场不允许卖空时,该投资组合的权重满足下式: s.t ∑w1t=1 (0≤wit≤1) (15) 其中wit(i=1,2,…,n)为第i个资产在t日的权重向量,Wt=(w1t,w2t,…,wnt)为第t日组合权重向量。根据Liu的研究[13],最小方差投资组合的权重最优解为: (16) 其中1为全1向量。 等比例风险投资组合是由Maillard等提出的[14],即主要通过调整权重使每个资产在投资组合中的风险比例相等。当资本市场不允许卖空时,该组合权数满足下式: s.t ∑w1t=1 (0≤wit≤1) (17) 2.各投资组合的收益和波动分析。将预测的160天的协方差阵ΣLasso和ΣRA-Lasso应用于投资组合时,为了比较二者的实际应用绩效,根据笔者的研究,将组合收益、组合标准差以及夏普比率作为衡量指标。夏普比率是由Sharpe提出的,其有效衡量了每单位风险所获得的收益。显然,标准差越小收益越高,夏普比率越高的投资组合越受投资者的青睐。表3给出了预测的协方差阵在投资组合中的应用效果。 表3 不同投资组合的平均收益、组合波动、Sharpe比率表 根据表3知,无论选择何种投资组合,较预测的协方差阵ΣLasso而言,由ΣRA-Lasso构造的投资组合的组合收益更高,组合波动更小,其夏普比率值也更高,从而说明了在收益一定的情况下,由预测的协方差阵ΣRA-Lasso构造的投资组合风险更小,或者说是在风险一定的情况下,由ΣRA-Lasso构造的投资组合的组合收益更高。 图2中Lasso表示的是由ΣLasso构造组合的Sharpe比率值,RA-Lasso表示的是由ΣRA-Lasso构造组合的Sharpe比率值。据图2易得,无论选择何种投资组合,由ΣRA-Lasso所构造的投资组合的Sharpe比率值显然要高于ΣLasso。 图2 动态Sharpe比率变化示意图 在大数据时代,随着数据可获得性的提高,金融数据的维度呈爆炸式的增长。如何估计高维金融数据的协方差阵已引起了学者们的广泛关注,但以往的研究大都是在数据服从正态分布的假定下进行的,而金融数据大多是服从厚尾分布的,极端风险出现的次数明显要多于正态分布。在估计高维金融数据的协方差阵时,考虑金融数据的厚尾特征,有助于发现市场异常走向,防范和化解金融极端风险。本文将RA-Lasso方法和乔列斯基分解法相结合,提出新的方法来估计高维厚尾金融数据的协方差阵(记为ΣRA-Lasso)。该方法首先通过乔列斯基分解法将复杂的高维协方差阵估计方法转化为一系列的回归模型;然后将基于惩罚Huber损失函数的稳健的lasso方法(RA-Lasso)法应用到这一系列的回归模型中,并将一些回归系数压缩为0以精简模型,达到降维之目的。RA-Lasso方法能够很好地估计高维厚尾数据的回归模型,因此将RA-Lasso方法应用到基于乔列斯基分解的回归模型中,在解决维数诅咒问题的同时,很好地克服了金融数据的厚尾特征对协方差阵估计的影响,明显提高了高维协方差阵的估计效率。通过模拟和实证研究发现,考虑了数据厚尾特征的ΣRA-Lasso方法明显优于其他协方差阵估计方法,并将其应用于投资组合时,投资者获得了更高的收益。 [1] 马学俊.GSIS超高维变量的选择[J].统计与信息论坛,2015(8). [2] 张景肖,李向杰,郭海明.HD-SIS超高维数据稳健变量筛选[J].统计与信息论坛,2016(4). [3] Fan J,Liao Y,Mincheva M.High Dimensional Covariance Matrix Estimation in Approximate Factor models[J].The Annals of Statistics,2011(6). [4] Fan J,Liao Y,Mincheva M.Large Covariance Estimation by Thresholding Principal Orthogonal Complements[J].Journal of the Royal Statistical Society,2013(4). [5] Cai T,Zhou H.Optimal Rates of Convergence for Sparse Covariance Matrix Estimation[J].The Annals of Statistics,2012(5). [6] Cai T,Liu W.Adaptive Thresholding for Sparse Covariance Matrix Estimation[J].Journal of the American Statistical Association,2011(106). [7] Wu W B,Pourahmadi M.Nonparametric Estimation of Large Covariance Matrices of Longitudinal Data[J].Journal of Biometrika,2003(4). [8] Li Y,Wang N,Hong M,Nancy D T,Joanne R,et al.Nonparametric Estimation of Correlation Functions Inlongitudinal and Spatial Data,with Application to Colon Carcinogenesis Experiments[J].The Annals of Statistics,2007(4). [9] Xue L,Zou H.Rank-Based Tapering Estimation of Bandable Correlation Matrices[J].Journal of Statistica Sinica,2014(1). [10] Fan J,Li Q,Wang Y.Robust Estimation of High-Dimensional Mean Regression[J].Journal of Statistics,2014(4). [11] Huber P J.Robust Estimation of a Location Parameter[J].The Annals of Mathematical Statistics,1964(35). [12] Wang L.The L1 Penalized LAD Estimator for High Dimensional Linear Regression[J].Journal of Multivariate Analysis,2013(9). [13] Liu Q.On Portfolio Optimization:How and When Do We Benefit from High-Frequency Data?[J].Journal of Applied Econometrics,2009(4). [14] Maillard S,Roncalli T,Teiletche J.On the Properties of Equally Weighted Risk Contributions Portfolios[J].Journal of Portfolio Management,2010(4).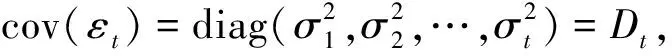
(二)调整参数α的选择
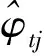
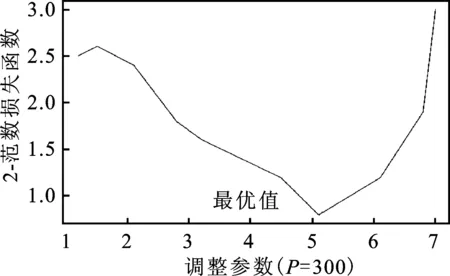
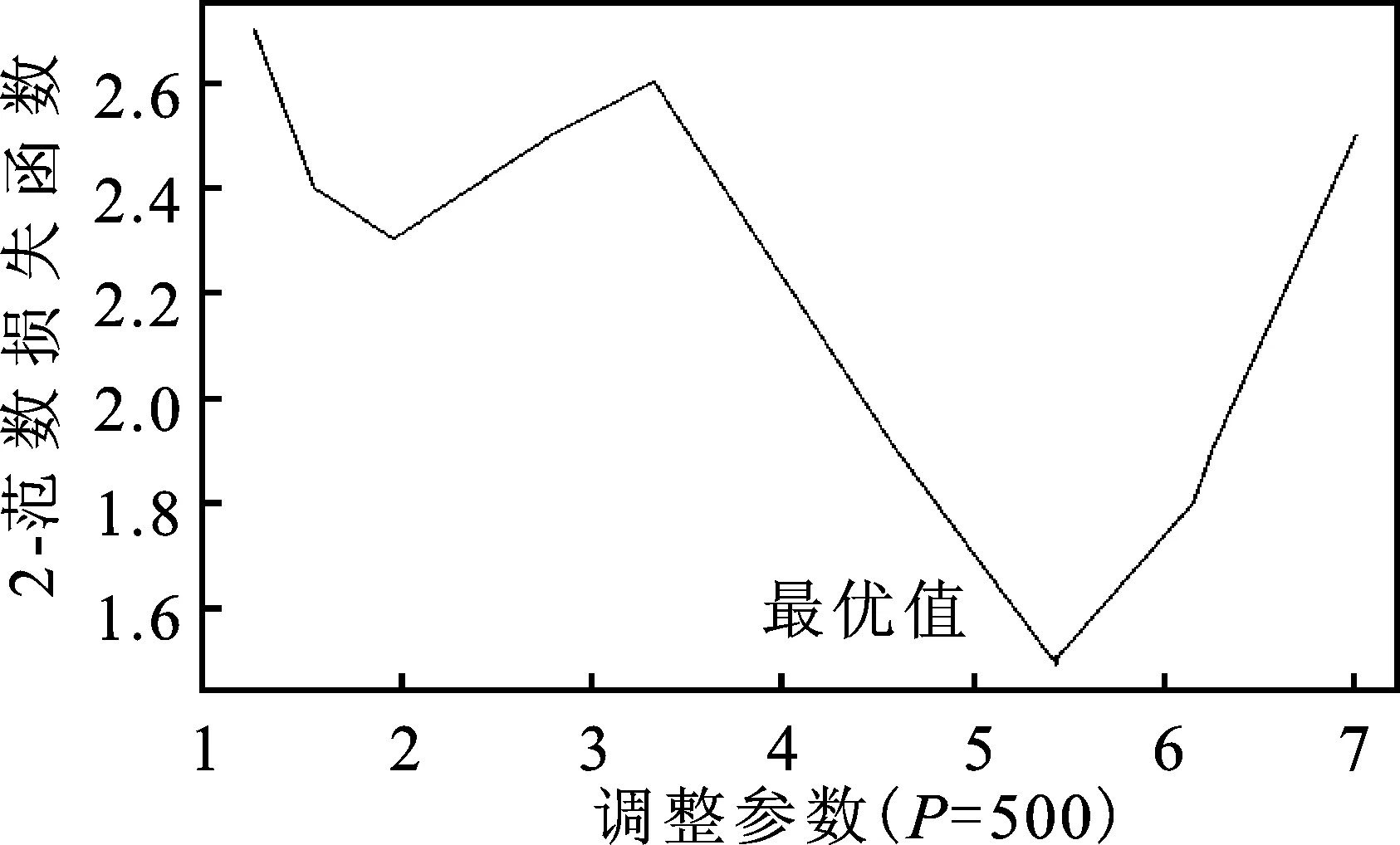
(三)ΣRA-Lasso协方差阵估计方法与其他方法的比较
四、实证研究
(一)股票收益率数据的正态性检验

(二)预测的动态条件协方差阵在投资组合中的应用研究
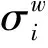

五、结 论

