基于可信度法求解区间双层线性规划问题

任 爱 红

(宝鸡文理学院 数学与信息科学学院, 陕西 宝鸡 721013)

双层规划是一类含有两层递阶结构的复杂系统优化问题. 其模型在网络设计、 经济管理和电力定价等实际问题中应用广泛[1-4]. 但由于双层规划的嵌套结构和NP-难特性, 导致求解该类问题很困难. 目前, 针对双层规划的研究主要集中在上下层目标函数和约束函数中所有系数都是实数的情形.

在实际应用中常存在各种不确定性, 可分别利用概率理论和模糊集理论描述两层递阶决策问题中存在的随机不确定性和模糊不确定性, 通过引入随机双层规划和模糊双层规划解决该类问题. 针对这两类不确定双层规划, 需要确定精确概率分布函数和隶属度函数. 区间数方法是一种简单有效地描述不确定性的方法, 它只需已知参数的上界和下界. 目前对区间双层规划的研究报道较少. 王建忠[5]根据决策背景, 提出了几类区间双层线性规划模型和最优解的概念, 并设计了相应的求解方法; Calvete等[6]针对仅上下层目标函数中含区间系数的双层线性规划, 提出了KBB和KBW两种极点算法, 分别求解原问题的最好最优解和最差最优解, 基于此给出上层目标函数的最优值范围; 任爱红等[7]设计了两种割平面法求解区间双层线性规划问题, 得出了最好最优解和最差最优解; 樊扬扬等[8]提出了一种基于双适应度函数评估的遗传算法, 对一类上层目标函数中带区间系数的双层规划问题进行求解. 本文考虑一类上下层目标函数和约束函数中所有系数均为区间数的双层线性规划问题. 为给决策者提供一个最优解, 先引入上下层目标函数的期望目标区间, 再基于区间数的可信度概念给出上下层目标函数的可信水平. 基于此, 提出区间双层线性规划可行域和最优解的概念. 对上下层规划分别采用极大极小算子, 将原区间双层线性规划转化为一个单层确定等价模型.

1 预备知识

定义1[9]记cI=[cL,cR]={x:cL≤x≤cR,x∈}, 称cI为一个区间数, 其中cL和cR分别是区间数cI的下界和上界. 特别地, 当cL=cR时, 区间数cI退化为一个实数. 称len(cI)=cR-cL为区间数cI的长度. 令I()表示全体区间数.

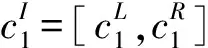
2 区间双层线性规划问题及其解的概念

考虑上下层目标函数和约束函数中所有系数均为区间数的双层线性规划问题：

(1)

其中x∈n和y∈m分别为上下层规划的决策变量;FI,fI:n×m→I()分别为上下层规划的目标函数均为n维区间向量均为m维区间向量均为区间数.

基于定义2中区间数之间的算术运算, 问题(1)中上下层目标函数已不再是一个精确的实值而是一个区间值, 同时约束函数是区间不等式约束, 因此问题(1)不是一个严格意义上的数学规划问题. 如何定义问题(1)的可行域以及上下层目标函数最优值的概念是处理这类不确定双层规划问题的关键, 而解决这两个问题涉及到不同区间数之间的排序. 目前已有许多比较和排序区间数的方法[11-12]. 考虑到不仅希望比较区间数之间的大小, 而且还可以度量区间数之间大小的程度, 同时符合决策者较精确的预期, 因此本文采用文献[10]提出区间数排序的可信度定义, 比较不同上下层决策变量下上下层目标函数的区间值以及区间不等式约束.

令问题(1)的约束域为

在实际应用中, 决策者常需要依赖于预先给定的某个期望目标获得一个最优解. 在该意义下, 基于定义3中可信度的概念, 下面给出区间双层线性规划问题(1)的可行域和最优解的概念.

称y*是问题(1)中下层规划的一个可信弱有效解.

IR={(x,y)∈n×m|(x,y)∈S,y∈M(x)}.

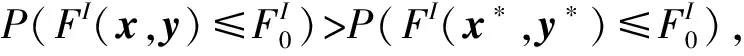
3 基于可信度法确定等价模型

(2)

其中:

令β表示上层规划目标函数的可信水平, 利用极大极小算子方法, 问题(1)可转化为如下问题:

(3)

结合问题(2),(3), 令α=min{λ,β}, 则问题(1)可转化为下列单层规划问题：

(4)

下面利用定义3中可信度法, 将问题(4)中所有不等式转化为下列确定不等式形式：

因此问题(4)可转化为下列确定数学模型：

(5)

定理1若问题(5)的最优解为(x*,y*,α*), 则(x*,y*)是问题(1)可信水平为α*的一个可信最优解.

令α*≤λ. 记

由定理1, 只需通过求解模型(5), 即可获得问题(1)的一个可信最优解. 注意到问题(5)是一个非线性规划问题, 通常可采用信赖域方法、 内点法、 可行方向法等求解这类问题. 本文利用MATLAB优化工具箱求解非线性规划问题(5).

4 数值实例

为表明本文所提方法的可行性, 考虑下列区间双层线性规划问题：

(6)

首先确定上下层目标函数的期望目标区间. 对于下层规划, 根据Tong[14]的最优值区间方法, 对给定的x, 可求得下层最好和最差最优值分别为7x-28和5x-6, 因此下层目标函数的期望目标区间可给定为[7x-28,5x-6]. 此外, 依据文献[15]中定理3.3, 可求得上层最好和最差最优值分别为-5.6和-1.5, 因此上层目标函数的期望目标区间确定为[-5.6,-1.5]. 由模型(5)知, 问题(6)可转化为相应的单层确定数学模型. 利用MATLAB优化工具箱, 可求得最优解为x*=3.471 3,y*=0,α*=0.057 5. 因此, 相应的上层目标函数最优值区间为[-3.471 3,-1.735 7], 且[-3.471 3,-1.735 7]⊆[-5.6,-1.5]. 显然所求的最优值满足边界条件.

综上可见, 本文提出的方法能灵活地为决策者提供在一定可信度下上层区间目标函数的最优值范围, 使所得结果具有较高的可行性.

[1] Gzara F. A Cutting Plane Approach for Bilevel Hazardous Material Transport Network Design [J]. Operations Research Letters, 2013, 41(1): 40-46.

[2] Calvete H I, Galé C, Oliveros M J. Bilevel Model for Production: Distribution Planning Solved by Using Ant Colony Optimization [J]. Computers & Operations Research, 2011, 38(1): 320-327.

[3] Labbé M, Violin A. Bilevel Programming and Price Setting Problems [J]. 4OR, 2013, 11(1): 1-30.

[4] Kalashnikov V V, Dempe S, Pérez-Valdés G A, et al. Bilevel Programming and Applications [J/OL]. Mathematical Problems in Engineering, 2015-03. http://dx.doi.org/10.1155/2015/310301.

[5] 王建忠. 区间线性双层规划方法研究 [D]. 天津: 天津大学, 2010. (WANG Jianzhong. Research on the Methods of Interval Linear Bi-level Programming [D]. Tianjin: Tianjin University, 2010.)

[6] Calvete H I, Galé C. Linear Bilevel Programming with Interval Coefficient [J]. Journal of Computational and Applied Mathematics, 2012, 236(15): 3751-3762.

[7] REN Aihong, WANG Yuping. A Cutting Plane Method for Bilevel Linear Programming with Interval Coefficients [J]. Annals of Operations Research, 2014, 223(1): 355-378.

[8] 樊扬扬, 李和成. 一类区间系数线性双层规划问题的遗传算法 [J]. 计算机应用, 2014, 34(1): 185-188. (FAN Yangyang, LI Hecheng. Genetic Algorithm for Solving Linear Bilevel Programming with Interval Coefficients [J]. Journal of Computer Applications, 2014, 34(1): 185-188.)

[9] Moore R E, Kearfott R B, Cloud M J. Introduction to Interval Analysis [M]. Philadelphia, PA: SIAM, 2009.

[10] 秦成燕, 李炜. 区间线性规划问题的可信度及其改进解 [J]. 杭州电子科技大学学报, 2011, 31(3): 74-77. (QIN Chengyan, LI Wei. Possibility Degree and Improvement Solution of the Interval Linear Programming [J]. Journal of Hangzhou Dianzi University, 2011, 31(3): 74-77.)

[11] Nakahara Y, Sasaki M, Gen M. On the Linear Programming Problems with Interval Coefficients [J]. Computer & Industrial Engineering, 1992, 23(1/2/3/4): 301-304.

[12] Sengupta A, Pal T K. On Comparing Interval Numbers [J]. European Journal of Operational Research, 2000, 127(1): 28-43.

[13] 史加荣, 刘三阳, 熊文涛. 区间数线性规划的一种新解法 [J]. 系统工程理论与实践, 2005, 25(2): 101-106. (SHI Jiarong, LIU Sanyang, XIONG Wentao. A New Solution for Interval Number Linear Programming [J]. Systems Engineering: Theory & Practice, 2005, 25(2): 101-106.)

[14] TONG Shaocheng. Interval Number and Fuzzy Number Linear Programmings [J]. Fuzzy Sets and Systems, 1994, 66(3): 301-306.

[15] Hamidi F, Mishmast N H. Bilevel Linear Programming with Fuzzy Parameters [J]. Iranian Journal of Fuzzy Systems, 2013, 10(4): 83-99.