定积分要的导学

■河南省开封市第二十五中学　张 涛

定积分的计算是高考的必考内容,尤其是求平面图形的面积,一直是近几年高考命题的热点。那么定积分究竟有哪些内容呢?我们一起来学习一下。

一、知识要点梳理

1.定积分的概念

一般地,如果函数f(x)在区间[a,b]上连续,用分点a=x0＜x1＜…＜xi-1＜xi＜…＜xn=b将区间[a,b]等分成n个小区间,在每个小区间[xi-1,xi]上任取一点ξi(i=1,2,中Δx为小区间长度),当n→∞时,上述和式无限接近某个常数,这个常数叫作函数f(x)在区间[a,b]上的定积分,记作f(x)dx,即分别叫作积分下限与积分上限,区间[a,b]叫作积分区间,函数f(x)叫作被积函数,x叫作积分变量,f(x)dx叫作被积式。

2.定积分的几何意义

从几何上看,如果在区间[a,b]上函数f(x)连续且恒有f(x)≥0,那么定积分f(x)dx表示由直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的曲边梯形的面积。这就是定积分(x)dx的几何意义。

3.定积分的性质

由定积分的定义,可以得到定积分的如下性质:

4.微积分基本定理

一般地,如果f(x)是区间[a,b]上的连续函数,并且F'(x)=f(x),那么(x)dx=F(b)-F(a)。这个结论叫作微积分基本定理,又叫作牛顿-莱布尼茨公式。

5.定积分在几何中的应用

定积分在几何中的应用主要是计算由两条曲线所围图形的面积。依照曲边梯形面积的求法,我们可以将求两条曲线所围图形的面积问题转化为求两个曲边梯形的面积问题,进而用定积分求出面积。

6.定积分在物理中的应用

①变速直线运动的路程:我们知道,做变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即s=(t)dt。

②变力做功:已知某物体在变力F(x)的作用下做直线运动,并且该物体沿着与F(x)相同的方向从x=a移动到x=b(b＞a),求变力F(x)所做的功W,与求曲边梯形的面积及求变速直线运动的路程一样,可用“四步骤”,即分割、近似代替、求和、取极限来解决,得到W=F(x)dx。

二、学习重点须知

学习重点主要包括定积分的几何意义,定积分的基本性质,运用微积分基本定理计算定积分,定积分的应用。

重点1：利用定积分的几何意义计算定积分

利用定积分的几何意义求:

图1

图2

点评:(1)利用定积分的几何意义求解时,常见的平面图形的形状是三角形、直角梯形、矩形、圆等可求面积的平面图形。(2)设函数f(x)在闭区间[-a,a]上连续,则若f(x)是偶函数,则f(x)dx=f(x)dx;若f(x)是奇函数,则f(x)dx=0。

(1)由曲线xy=1,直线y=x,x=3所围成的封闭平面图形的面积为()。

(2)如图3,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为。

解析：(1)由曲线xy=1,直线y=x,x=3所围成的封闭的平面图形,如图4所示。

图3

图4

(2)因为函数y=ex与函数y=lnx互为反函数,其图像关于直线y=x对称,且函数y=ex与直线y=e的交点坐标为(1,e),所以阴影部分的面积为

点评:利用定积分求平面图形面积的步骤:(1)根据题意画出图形;(2)借助图形确定出被积函数,求出交点坐标,确定积分的上、下限;(3)把曲边梯形的面积表示成若干个定积分的和;(4)计算定积分,写出答案。

重点2：定积分在物理中的应用

(1)已知变速直线运动的方程,求在某段时间内物体运动的位移或者经过的路程,就是求速度关于时间的函数的定积分。

(2)利用定积分求变力做功的问题,关键是求出变力与位移之间的函数关系,确定好积分区间,得到积分表达式,再利用微积分基本定理计算即可。一物体在变力F(x)=(x的单位:m,F的单位:N)的作用下,沿着与力F相同的方向从x=0运动到x=5处,求变力所做的功。

解析：变力F(x)所做的功为:

=12+60=72(J)。

点评:(1)对于给出物体在变力作用下沿与力相同方向运动的变力做功问题,可直接用定积分求解,计算公式W=∫baf(x)dx。(2)注意必须将力与位移的单位换算为N与m,功的单位才为J。

三、学习难点突破

难点1：利用微积分基本定理求定积分

求函数f(x)在某个区间上的定积分时,要注意:

(1)掌握基本初等函数的导数以及导数的运算法则,正确求解被积函数的原函数。

(2)精确定位积分区间,分清积分下限与积分上限。

计算下列定积分:

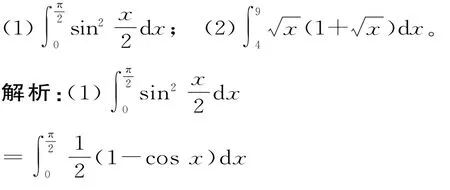
点评:微积分基本定理揭示了导数与定积分之间的关系,即求定积分与求导互为逆运算,求定积分时只需找到被积函数的一个原函数。

难点2：定积分在几何中的应用

对于简单图形的面积求解,我们可以直接运用定积分的几何意义,应注意:(1)确定积分上、下限,一般为两交点的横坐标;(2)确定被积函数,一般是上曲线与下曲线对应函数的差。

这样所求的面积问题就转化为运用微积分基本定理计算定积分了。

求抛物线y2=8x(y＞0)与直线x+y-6=0及y=0所围成图形的面积。

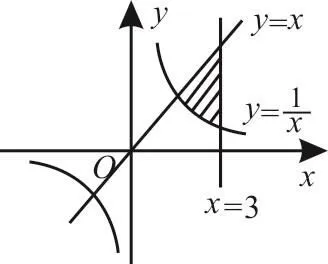
图5

点评:用定积分求较复杂的平面图形的面积时,一要根据图形确定把x还是y作为积分变量,同时,由曲线交点确定好积分上、下限;二要依据积分变量确定好被积函数,积分变量为x时,围成平面图形的上方曲线减去下方曲线为被积函数,积分变量为y时,围成平面图形的右方曲线减去左方曲线为被积函数;三要找准原函数。