浅析最短路径问题

徐紫鸣

（安阳正一中学 河南安阳 455000）

引言

我们在几何的学习中常常会遇见很多种和最短路径相关的有趣例题，例如口渴的马到河边饮水如何走距离最短，在相近的村庄中间建造桥梁怎样才能便利所有的村民，蚂蚁搬运大米怎么才能最省力气。这类问题就是几何中的求最值问题，对于求最值问题的解题方法，我们通常会应用到的知识是：两点间线段最短的定理、三角形的三边关系、垂线段最短的性质以及轴对称的解题方法和线段翻折平移的解题方法。其中还涉及了转化的数学思想应用，转化思想方法能将空间立体几何问题转化为平面几何问题所以在解题思路上逻辑很清晰。[1]

一、饮马问题[2]

将军饮马的问题早在古罗马时代就已经存在，传说一位罗马的将军专程去拜访亚历山大城中一位名叫海伦的学者，向这位精通数学的学者请教了一个问题：我每日都要从军营中出发，先骑马到河边让马儿喝水，然后再骑着马到与军营同侧的另一个营地去开会，怎样走才能让马儿走的路途最短呢？

解析：这个问题的解决办法十分简单，通过学过的知识我们知道，两点间最短的距离就是分别以两个点为端点连结产生的线段，但由于军营M和营地N都在小河的同一侧，将军每日还需在小河边饮马，我们可以通过做军营M关于小河L的对称点将线段PM等换成线段PM’，因为只有P点在直线MN上时才会使PM+PN有最小值也就是我们所求的最佳饮马地点，很明显由于饮马的地点P只能在小河L上，故首先做营地M关于小河L的对称点M’，然后连结M’N交小河L于点P，此时M’、P、N三点位于同一条直线上，PM’+PN具有最小值，点P就是所求的最佳饮马地点。

关于饮马问题还有很多变形，上述例题可总结为是在一条固定直线和同侧的两个固定的点中求解最短距离。其中运用了轴对称的性质，通过等线段的替代，将所求路线的长度转化为了两个定点之间的距离。与之类似的还有在一条固定直线和异侧两个固定的点中求解最短距离，由于点分别位于直线两侧可直接根据“两点间线段最短”连结两个异侧的点求解。当然如果在这类模型中加入动点就会变得稍微复杂，但解题的思路是不变的，都是通过轴对称的性质、翻折或是平移的运动，将其中一些线段进行转化变成更基本的模型，再来求解。

二、蚂蚁吃大米问题

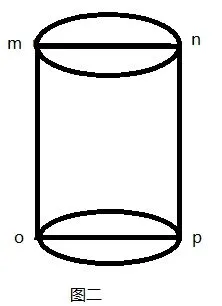
如图二所示，一只蚂蚁正处于圆柱体的o点，发现了n点有一粒大米，且mnop是圆柱体的一个横截面，底面半径为12/πcm，圆柱体高为8cm，求蚂蚁从o点出发吃到n点的大米最短需要爬几厘米？

解析：圆柱体的侧面展开后是一个长方形（图三），且蚂蚁所处的o点和大米所处的n点都在展开的长方形上，根据“两点间线段最短”连结on即可得出最短距离。弧op的长度为：1/2（πr）=6cm，线段np=8cm，故线段on=10cm。即蚂蚁从o点出发吃到n点的大米最短需要爬10cm。

对于此类在立体图形中求最短距离的问题，通常可以将立体图形沿着棱或者母线剪开，将其展开转化为平面图形求解，例如题中圆柱体侧面展开图就是长方形，圆锥的侧面展开图是扇形等等。再通过“两点间线段最短”画出最短路线解答题目就会简单很多。

当然，解决最值问题时一定要认真审题，例如同样是蚂蚁吃大米的问题，将上述题目中的圆柱体改为长宽高分别为3cm、4cm、5cm的长方体，但是要求蚂蚁只能从长方体的棱爬过，求从A点出发吃到C1点大米的最短距离（图四）。在这个问题中，由于蚂蚁只能从长方体的棱爬过，就不能利用立体图形侧面展开图将出发点和目的点转化于同一平面连结求解。按照题中要求，此时蚂蚁吃到大米爬过的最短距离至少应当包括长方体的长宽高各一条，故蚂蚁吃到大米的最短距离应当为3+4+5=12cm。

结语

几何中的最值问题一直是学习中的热点问题，对于此类问题的学习，在牢固掌握相关知识点的基础上我们应当善于应用转化的数学思想，将看似陌生复杂的问题转化成我们熟悉简单的问题再来解答，这样就会让解题变得更加高效和顺利。