双分数Ornstein-Uhlenbeck过程下欧式幂型期权定价模型

武 涛, 薛 红

(西安工程大学 理学院,陕西 西安 710048)

0 引 言

随着期权定价的深入研究, 股票价格遵循 Ornstein-Uhlenbeck(简称 O-U)过程也被逐渐引入金融市场模型中.O-U过程是一类重要的移动平均过程, 最早由Sato和Yamazato[13]在1982年提出. 许多学者也对股票价格遵从O-U过程的期权实行了定价[14-16].幂型期权是奇异期权的一种, 它在到期日的价值不是用股价与执行价格的差值,而是股票价格在到期日的某个指数幂与执行价格之间的差值. 与传统期权所不同的是, 幂型期权有能够增强期权风险的效果, 同时也有很大的变通性, 可以满足各样风险喜好的投资者的需求. 近几年不少学者研究幂型期权[17-19]，并把O-U过程引入到模型中[20-24].本文借助双分数Brown运动相关理论, 引入Ornstein-Uhlenbeck过程,假设股票价格服从双分数布朗运动和Ornstein-Uhlenbeck过程下驱动的随机微分方程,借助双分数布朗运动和Ornstein-Uhlenbeck过程下金融市场数学模型,运用保险精算方法,推导出欧式幂型期权定价公式和欧式上封顶及下保底幂型期权定价公式, 丰富了期权定价的理论.

1 双分数Ornstein-Uhlenbeck过程下金融市场数学模型

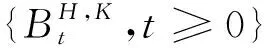
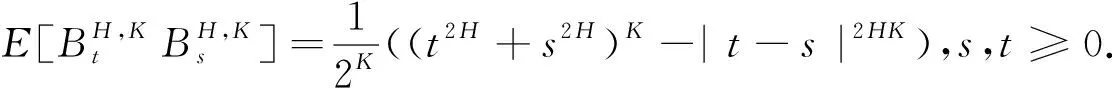
假定股票价格{St,t≥0}遵循双分数Ornstein-Uhlenbeck过程

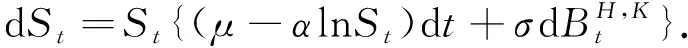
(1)

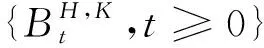
定理1 随机微分方程(1)的解为

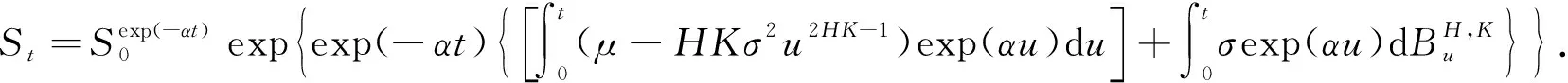
(2)

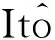
两边积分有

可得

得证.

注:当α=0时,可得双分数布朗运动环境下股票价格过程:

定义2[16]价格过程{St,t≥0}在[0,t]上的期望回报率β(u),u∈[0,t]定义为

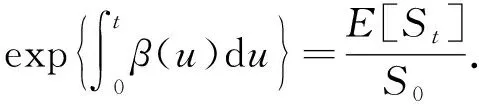
(3)

定理2 股票价格{St,t≥0}在[0,t]上的期望回报率β(u),u∈[0,t]满足

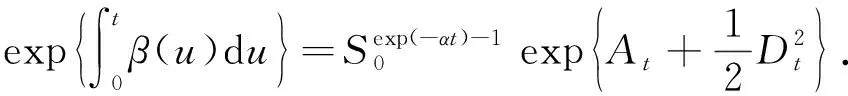
(4)

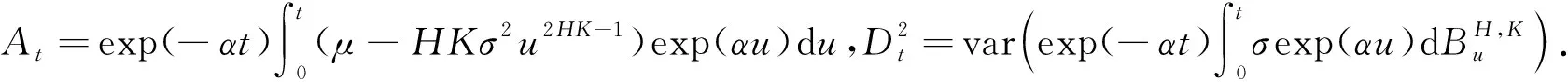
当α=0时,双分数布朗运动环境下股票价格期望回报率为β(u)=μ,u∈[0,t]

证明由定理1知

由于

ξ

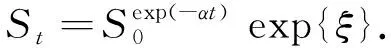
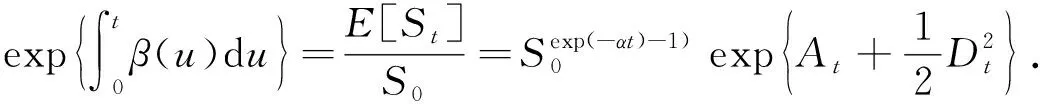
得证.

2 欧式幂型期权定价

定义3[13]欧式幂期权在T时刻的价值定义为:股票到期日价格按期望回报率折现值的幂与执行价(看作是无风险资产债券)按无风险利率折现值的差在股票价格实际分布的概率测度下的数学期望, 这一定价称为期权的保险精算定价. 用C(K,T)和P(K,T)分别表示执行价格为K, 到期日为T的欧式看涨幂期权和看跌幂期权在t=0时刻的价格, 则根据精算定价方法知欧式幂型期权的保险精算价值

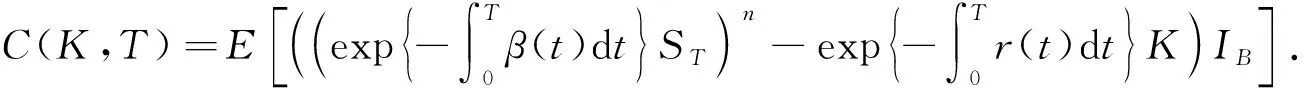
(5)

(6)

其中

定理3 执行价格为K, 到期日为T的欧式看涨和看跌期权在t=0时刻的保险精算价值

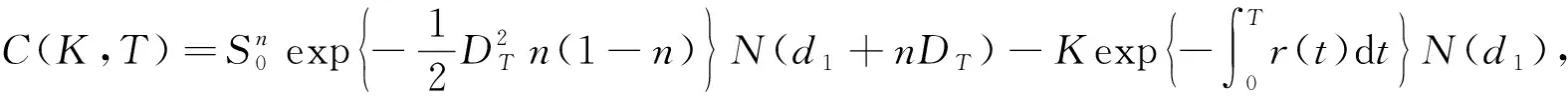
(7)

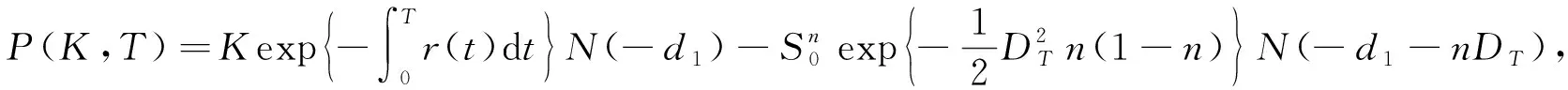
(8)

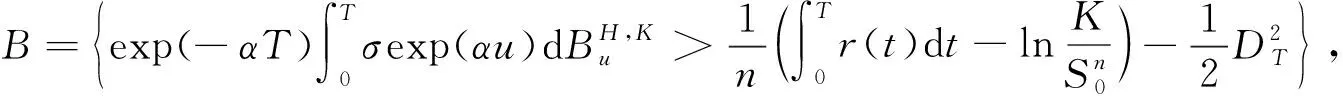
且

则

从而B={η>d1}.

由于

(9)

其中

由此可得

同理可得

推论1 当K=1时, 可得分数O-U过程下的欧式看涨和看跌幂型期权定价公式为

推论2 当α→0时, 可得双分数布朗运动环境下的欧式幂型期权定价公式；当α→0,K=1时, 可得分数布朗运动环境下的欧式幂型期权定价公式(见文献[21]).

3 欧式上封顶及下保底幂型期权定价

定理4 设L为给定的期权上限, 则欧式看涨和看跌上封顶幂型期权在0时刻保险精算价格为

其中

证明欧式上封顶看涨幂型期权的损益为

(14)

利用定理3可得结果.

定理5 设R为给定的期权下限, 则欧式下保底看涨和看跌幂型期权0时刻保险精算价格为

证明欧式下保底看涨幂型期权的损益为

(17)

利用定理3可得结果.

注1 当L→+∞, 或L=0时, 可得双分数O-U过程下欧式看涨幂型期权定价公式.

推论3 当K=1时, 可得分数O-U过程下的欧式上封顶及下保底n次幂型期权定价公式.

推论4 当n=1时, 可得双分数O-U过程下的欧式上封顶及下保底幂型期权定价公式.

推论5 当α→0,K=1时, 可得分数布朗运动环境下的欧式上封顶及下保底幂型期权定价公式[25].

参考文献(References)：

[1] BACHELIER LOUIS.Theorie de la speculation[J].Annals de L′Ecole Normale Superieure,1900,17:21-86.

[2] BLACK F,SCHOLES M.The pricing of option and corporate liabilities[J].Journal of Political Economy,1973,13(3):637-659.

[3] HOUDRE C,VILLA J.An example of in infinite dimensional quasihelix[J].Contemporary Math,2003,336:195-201.

[4] RUSSO F,TUDOR C.On the bi-fractional Brownian motion[J].Stochastic Processes and their Applications,2006,116(5):830-856.

[5] 肖玮麟,张卫国,徐维东.双分式布朗运动下股本权证的定价[J].系统工程学报,2013,28(3):348-354.

XIAO W L,ZHANG W G,XU W D.Pricing equity warrants in a bifractional Brownian motion[J].Journal of Systems Engineering,2013,28(3):348-354.

[6] 薛红,文福强，李巧艳.分数布朗具有随机寿命的欧式未定权益的定价[J].纺织高校基础科学学报，2006，19(4):351-335.

XUE H,WEN F Q,LI Q Y.Pricing on European contingent claim with stochastic life under fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2006，19(4):351-335.

[7] 李巧艳，薛红.分数布朗运动环境下的最优投资组合[J].纺织高校基础科学学报，2007，20(1):30-32.

LI Q Y,XUE H.Optimal portfolio in fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2007，20(1):30-32.

[8] 何永红，薛红，王晓东.分数布朗运动环境下再装期权的保险精算定价[J].纺织高校基础科学学报，2012，25(3):384-387.

HE Y H,XUE H,WANG X D.The actuarial approach to reload option pricing in fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2012，25(3):384-387.

[9] 李萍，薛红，李琛炜.分数布朗运动下具有违约风险未定权益定价[J].纺织高校基础科学学报，2012，25(3):462-466.

LI P,XUE H,LI C W.Credit-risky claims pricing in fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2012，25(3):462-466.

[10] 衡晓,薛红.次分数布朗运动环境下脆弱期权定价[J].纺织高校基础科学学报，2015，25(4):447-451.

HENG X,XUE H.Vulnerable option pricing in sub-fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2015，25(4):447-451.

[11] 淡静怡， 薛红.双分数布朗运动环境下的篮子期权定价[J].纺织高校基础科学学报，2016，29(4):460-464.

DAN J Y,XUE H.Pricing of basket option in bi-fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2016，29(4):460-464.

[12] 刘淑琴,薛红.双分数布朗运动环境下汇率连动期权定价[J].纺织高校基础科学学报，2017，30(4):522-526.

LIU S Q,XUE H.Quanto option pricing in bi-fractional Brownian motion environment[J].Basic Sciences Journal of Textile Universities，2017，30(4):522-526.

[13] SATO K.YAMAZATO M.Stationary processes of Ornstein-Uhlehbeck type[C]//Proceedings of 4th USSR-Japan Symposium.Berlin:Springer,1982.

[14] 闫海峰,刘三阳.股票价格遵循Ornstein-Uhlehbeck过程的期权定价[J].系统工程学报,2003,18(6):547-551.

YAN H F,LIU S Y.Pricing options on stocks driven by Ornstein-Uhlenback process[J].Journal of Systems Engineering,2003,18(6):547-551.

[15] 赵巍,何建敏.股票价格遵循分数Ornstein-Uhlenbeck过程的期权定价模型[J].中国管理科学,2007,15(3):1-5.

ZHAO W,HE J M.Model of option pricing driven by fractional Ornstein-Uhlenback process[J].Chinese Journal of Management Science,2007,15(3):1-5.

[16] 孙玉东,薛红.分数跳-扩散环境下欧式期权定价的Ornstein-Uhlenbeck模型[J].经济数学,2009,26(3):23-28.

SUN Y D,XUE H.Ornstein-Uhlenbeck model of opean option pricing in fractional jump-diffusion environment[J].Mathematics in Economics,2009,26(3):23-28.

[17] 周圣武,刘海媛.分数布朗运动环境下的幂期权定价[J].大学数学,2009,25(5):69-72.

ZHOU S W,LIU H Y.Power option pricing in a fractional Brownian motion[J].College Mathematics,2009,25(5):69-72.

[18] 王亚军,周圣武,张艳.基于新型期权——欧式幂期权的定价[J].甘肃科学学报,2005,17(2):21-23.

WANG Y J,ZHOU S W,ZHANG Y.The pricing of European power options[J].Journal of Gansu Sciences,2005,17(2):21-23.

[19] 陈万义.幂型支付的欧式期权定价公式[J].数学的实践与认识,2005,35(6):52-55.

CHEN W Y.The pricing formulas of European options with power payoffs[J].Mathematics in Practice and Theory,2005,35(6):52-55.

[20] 刘兆鹏,刘钢.基于O-U过程具有不确定执行价格的期权保险精算定价[J].杭州师范大学报(自然科学版),2011,10(4):316-319.

LIU Z P,LIU G.Actuarial approach of option pricing with change exercise price based on Ornstein-Uhlenbeck process[J].Journal of Hangzhou Normal University (Natural Science),2011,10(4):316-319.

[21] 赵佃立.分数布朗运动环境下欧式幂期权的定价[J].经济数学,2007，24(1):22-26.

ZHAO D L.Pricing of european power options in multidimensional fractional Brown motions environment[J].Mathematics in Economics,2007，24(1):22-26.

[22] 徐峰,郑石秋.混合分数布朗运动驱动的幂期权定价模型[J].经济数学,2010,27(2):8-12.

XU F,ZHENG S Q.Model of power option pricing driven by mixed fractional Brownian motion[J].Mathematics in Economics,2010,27(2):8-12.

[23] 赵攀.基于指数O-U过程的幂型欧式期权定价[J].贵州师范大学学报(自然科学版)，2014，37(1):1386-1390.

ZHAO P.Pricing of power European options based on the exponential Ornstein-Uhlenback process[J].Journal of Guizhou Normal University(Natural Sciences),2014，37(11):1386-1390.

[24] 闫海峰,刘三阳.广义Black-Scholes模型定价新方法:保险精算方法[J].应用数学和力学,2003,24(7):730-738.

YAN H F,LIU S Y.New method to option pricing for the general black-scholes model:An acturarial approach[J].Applied Mathematics and Mechanics,2003,24(7):730-738.

[25] 刘海媛,周圣武,索新丽.标的资产价格服从分数布朗运动的几种新型期权定价[J].数学实践与认识,2008,38(15):54-59.

LIU H Y,ZHOU S W,SUO X L.The pricing formulas of exotic options in a fractional Brownian motion[J].Mathematics in Practice and Theory,2008,38(15):54-59.