关于根式函数的多值性探讨
王振华,张为元,贺 雯
(咸阳师范学院数学与信息科学学院,陕西咸阳 712000)
从柯西时期开始,复变函数论已经有150年的历史了,已经深入到了数论、微积分方程等学科,并且在实际问题中得到了广泛的应用,其基础内容已经成为理工科专业的必修课程。2000年,金庭枝和王长庆[1]利用幅角函数证明了初等根式函数的枝点判定定理,并得到了一个求解根式函数单值分支的方法;2006年,朱顺东[2]关于函数的辐角在所给曲线上的改变量做了说明和注解;2010年,张忠诚和柳翠华[3]给出了确定多值函数单值解析分支值的步骤和方法;2015年,段辉明等[4]关于多值函数的教学提出了良好的建议;2016年,何美[5]、王金花[6]针对多值函数单值解析分支方面的计算做了归纳和总结。这些文献都涉及到了G平面,但都没有给出清晰准确的定义。为此,重新阐述了G平面的概念,并以根式函数为例讨论了G平面的结构和应用。
1 根式函数的单值分支
定义1设E为一复数集,若对E内每一个复数z,有惟一确定的复数ω与之对应,则称在E上确定了一个单值函数ω=f(z)(z∈E)。如对E内每一复数z,有几个或无穷多个ω与之对应,则称在E上确定了一个多值函数ω=f(z)(z∈E)。E称为函数ω=f(z)的定义域。ω值的全体所成集M称为函数ω=f(z)的值域。[7]
定义2对某个多值解析函数ω=f(z),若满足:在z=a的充分小的一个邻域内,作一条包围该点的简单闭曲线C,当z从C的某点出发,绕C连续变化一周而回到出发点时,f(z)从一个值变到另一个值,则称此点为多值解析函数 f(z)的支点。连接f(z)全体支点的曲线称为 f(z)在z平面上的支割线。[8]
定义3将z平面沿x负半轴割破(包括原点)所得的平面称为G平面。可以表示为
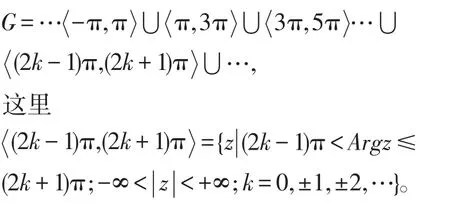
规定G平面上复数辐角主值的范围为-π<θ0<π。

k可以取n个值,故一个复数z对应n个函数值,它们位于半径为nr的圆周上,相邻两个函数值之间的张角为。在G平面上,动点z无法穿过支割线,也就不能绕原点z=0转一周,函数也就不能在G内同一点取不同的函数值,即在G内就能够分出该函数的单值分支。现以ω= z3为例,说明怎样分出根式函数的单值解析分支。我们令
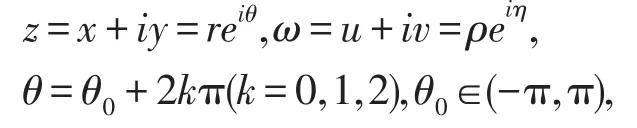
θ0为z的辐角主值。对任意的z∈G,其辐角θ必属于G中的一个区间。

(1)当 k=0时,此时则< η, 如图1所示:

图1 k=0时的单值分支
(2)当 k=1时,此时
θ=θ0+2π,ω=则如图2所示:
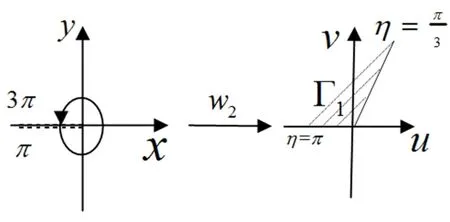
图2 k=1时的单值分支
(3)当k=2时,此时
θ=θ0+4π,ω=
则π<η<π,如图3所示:
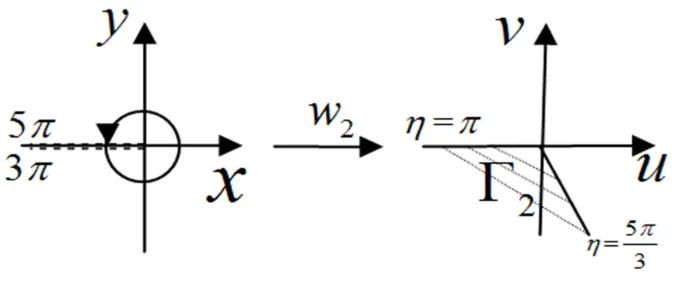
图3 k=2时的单值分支
(4)当 k=3时,此时
θ=θ0+6π则如图4所示:
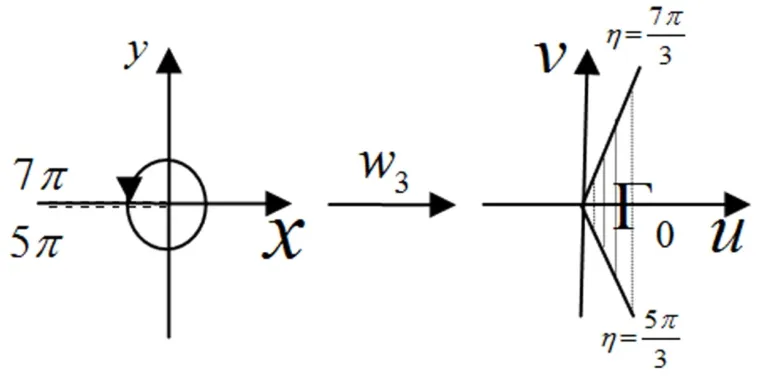
图4 k=3时的单值分支
不难发现,当k=0,3,6,9,…时对应ω平面中同一个角形区域Γ0,当k=1,4,7,10,…时也对应ω平面中同一个角形区域Γ1,当k=2,5,8,11,…时对应ω平面中同一个角形区域Γ2,我们发现对任意的z∈G,必然存在k0∈{0 ,1,2,3,…},使得当
z∈ (2k-1)π,(2k+1)π 时,ω=3z的图像必为
00三个分支Γ0,Γ1,Γ2中的某一个。
根据上面的讨论,根式函数中变量z对应的3个函数值分别分布在w平面上的3个角形区域Γk(k=0,1,2)内。每一个角形区域Γk都称为根式函数的一个单值分支。那么,如果取一个固定的k,即选定一个固定的角形区域Γk,函数是否就是G平面到角形区域Γk的单值分支呢?
定理1在G平面上,根式函数ω=3z可以分出3个不同的单值分支函数
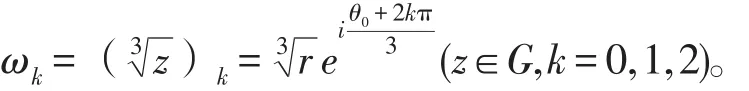
证明令 z=r eiθ1,z=r eiθ2,对任意的z,z∈且 z1≠z2,它们对应的函数值分别为
我们把z1≠z2分两种情形讨论:
当 r1≠r2时,显然 wk1≠wk2,即当r1=r2,θ1≠θ2时,因为
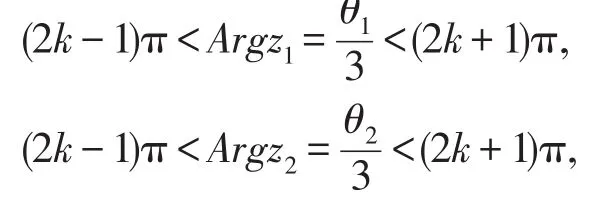
又因为 Argz1≠Argz2,所以是定义在G平面上的单值函数。
如图5左图所示,z0是上的某一点,原点z=0包含在闭曲线的内部。这时穿过了负实轴。于是,当变点z从z0出发,沿正或负方向绕一周后,z0的辐角就增加或减少了2π,z的像点ωk=(nz)k就不能回到它们的原来位置了,而是如图5中的虚线路径所示,由一支变化到另外一支,即
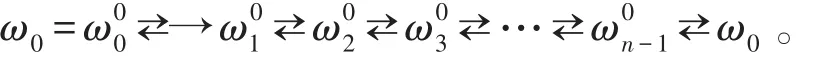
因此,在包含了原点z=0的复平面上,ω=nz就不能分成n个相互独立的单值解析分支,也就是说根式函数ω=nz在支点邻域内无单值性。
但如果割破z平面,则函数ω=nz将不再有支点,此时只要取定一个k的值,就得到一个以Γk为值域的单叶函数(如图5右实线图所示):
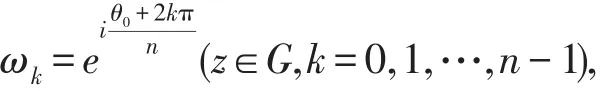
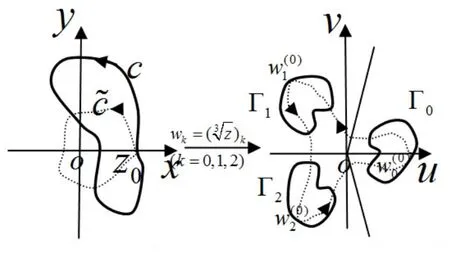
图5 支点与多值性的关系
ωk这是的n个单值分支函数,其中k=0的一支称为 zn的主值支。
2 证明的单值分支函数的解析性
定理2设
f(z)=u(r,θ)+iv(r,θ),z=reiθ,z∈G。如果 u(r,θ),v(r,θ)在点(r,θ)是可微的,且满足极坐标的C-R方程:
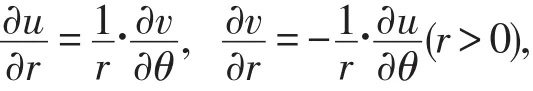
则 f(z)在点z是可微的,并且
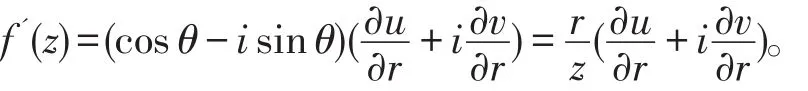
证明设 z=x+iy=reiθ, 则
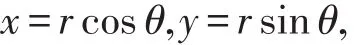
从而
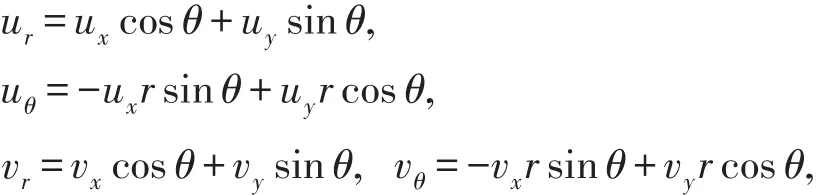
再由可得
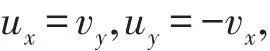
因此可得 f(z)在点z可微且
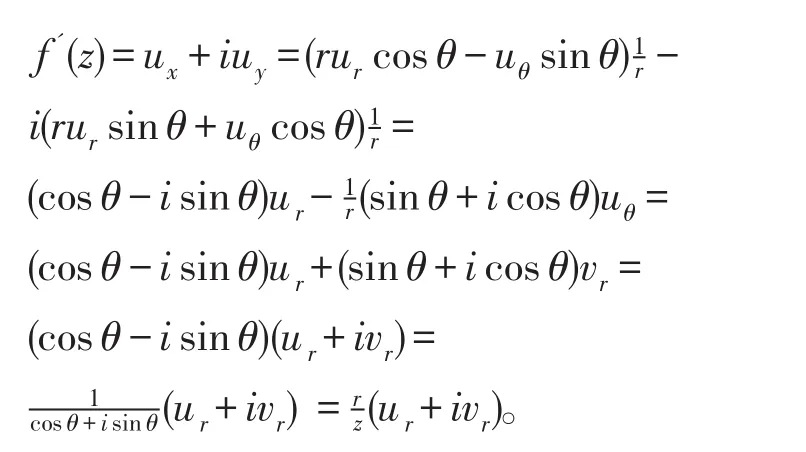
定理3根式函数w= zn的n个单值分支wk=(zn)k(k=0,1,2,…,n-1)在G平面上是解析的。
证明对任意的 z∈ G,设 z=rei(θ0+2kπ),
这里-π<θ0<π。因为
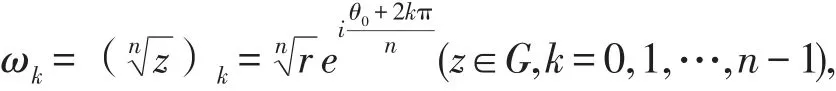
所以ωk=( zn)k这一单值分支函数的实部及虚部分别为

它们在G内皆为r,θ0的可微函数,并且
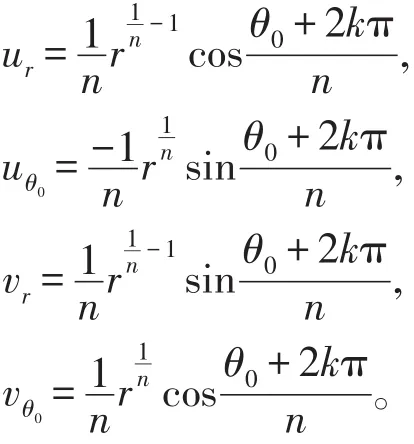
利用变换θ=θ0+2kπ,我们发现wk的实部及虚部在G内满足极坐标的C-R方程
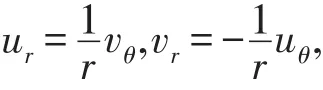
由定理1知wk=(zn)k在点z可微,并且
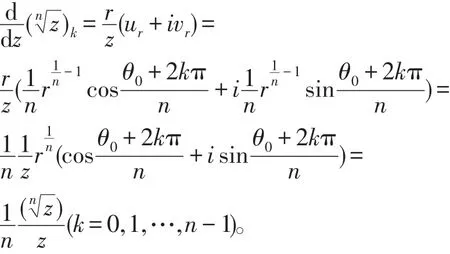
由z在G平面上的任意性可知,wk=(zn)k在G平面上处处可微,即在G平面上解析。
例 设ω= z3定义在从原点起沿负实轴割破的z平面上,并且ω(i)=-i,试求ω(-i)之值。
解因为G为从原点起沿负实轴割破的z平面,所以由定理1和定理3知,G为ω= z3的单值解析区域。设
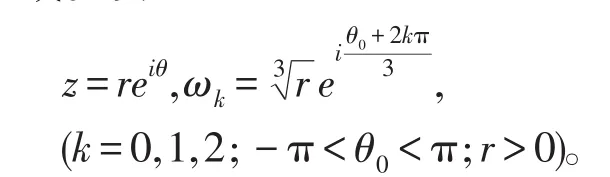
当 z=i时,要使成立,必须k=2。所以满足初始条件ω(i)=-i的单值解析分支为
(2)求 ω2(-i)。
因为 z=-i,所以所以
(1)由已知条件定k。
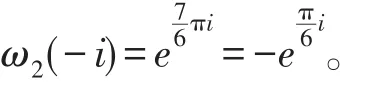
3 总结
常见的初等多值函数有根式函数、对数函数、反双曲函数与反三角函数等,多值函数一直都是复变函数教学中的一个难点。目前多复变分析是复变函数论研究的热点,它广泛地应用了李群、代数几何、拓扑学、微分几何学和微分方程等相关学科中的方法和概念,与单复变函数有着显著的区别。
[1]金庭枝,王长庆.多值函数的单值解析分支[J].辽宁师范大学学报(自然科学版),2000,23(2):217-21.
[2]朱顺东.关于求根式函数单值解析分支上辐角的一点注记[J].安徽师范大学学报(自然科学版),2006,29(4):299-331.
[3]张忠诚,柳翠华.确定多值函数单值解析分支值的一种简易方法[J].长春师范学院学报(自然科学版),2010,29(5):3-5.
[4]段辉明,张清华,李玲.有关多值函数的教学[J].高师理科学刊,2015(8):60-62.
[5]何美.多值函数单值解析分支上计算函数值的一个注记[J].山西大同大学学报(自然科学版),2016,32(4):1-2.
[6]王金花.一类多值函数的单值解析分支[J].沧州师范学院学报,2016,32(1):17-19.
[7]钟玉泉.复变函数论(第四版)[M].北京:高等教育出版社.2013:65-85.
[8]赵志勇,薛运华.复分析(第三版)[M].北京:机械工业出版社.2006:70-76.

