浅谈原创试题对课堂教学的作用

安徽 蒋玉芳 张 威

原创试题与课堂教学其实是相辅相成的.从课堂的学生探究活动中、从课堂教学里的“失败处”、从学生巧妙的回答中都可以获取原创试题的素材.同样原创试题对课堂教学也有着非常重要的作用.因为不同层次的学生、不同阶段的学生所需求试题的难度是不同的.每个学生都有适合自己的试卷、习题，当学生与题搭配成功时，那么此题将使学生的学习效果达到最大化.所以笔者认为在平时的教学中，教师应该多一些原创题，这样才能使得学生和题搭配成功，这样的课堂才会更高效.那么原创题对课堂教学到底有哪些具体的作用呢？以下是笔者的个人感受.

一、巩固新知，激发学生学习的兴趣

一线教师都知道，在讲授新知时，需要寻找典型例题对新知进行诠释，而往往教辅或教材上的例题或习题并不适合自己所教授的学生，此时需要一道既能让学生巩固新知，又能适合当前学生难易梯度的典型例题.那么什么样的试题才算是一道典型例题呢？一道典型例题应该不是所有学生都难以“下咽”的苦果，恰好相反，应该是所有学生“品尝”时感觉有话可说、有话要说的“菜肴”.典型例题不仅要能巩固新知，同时也要能增强学生的学习自信心，激发学生的学习兴趣.这就需要教师根据自己学生的实际情况命制试题.

例如，教师在讲解函数f(x)=Asin(ωx+φ)+b(A,ω>0,

φ,b∈R)的图象和性质时，有些基础弱的学生对如何求A,ω,φ,b的值掌握得不好.特别对代入特殊点求φ时，为什么要强调最好代最值点，而不是零点百思不得其解.此时就需要一道适合他们且有针对性的题目来巩固，同时激发他们的学习兴趣.这时教师可以原创一道.

( )

【命题意图】此题以生活中的实际物体为模型，极大地激发了学生学习数学的兴趣.从能力角度来看，此题不仅培养了学生阅读理解能力，而且也培养了学生数据处理和计算能力.从知识层面来看，此题突出了教师的实际意图，同样更好地诠释了A,ω,φ,b的实际意义.

【原创例题2】已知函数f(x)=2sin(2x+φ)(-π<φ<π)的部分图象如图所示，则φ=________.

【命题意图】此原创题的图象和以往的陈题图象差别很大，其用意就是“引导”学生代零点求φ，让学生“真正地”犯一次错.此题不仅培养了学生的数形结合思想，而且也培养了学生转化与化归的数学思想.

【点评】此时有的学生不去考虑增根问题，那么就错了.若有学生想到增根问题，又要花时间去排除增根.那么通过代入最值点，是否就不会出现增根呢？请看下面【正解】.

二、突破教学重难点，使课堂教学更高效

教师在讲授新课时，会发现有些重难点仅靠对概念的细化讲解，达不到预想的效果，此时需要配备例题进行具体化，让学生由浅入深，但是如果配备的例题不得当，没有充分考虑到学生的认知能力，学生的理解和掌握依然会遇到困难.而教师在充分了解当前学生实际水平的情况下，命制的例题就再合适不过了.同时作为命题者，在讲解此题时必能更透彻，因为他比别人更理解此题的本质，以及思考的方向.如：几何体的外接球问题一直是高考的重点和难点，而学生在求几何体的外接球半径时，往往会“有话说，但又说不到点子上”.如笔者设置的如下原创题.

笔者知道如果把这样一道题“甩出去”，估计很多学生都无法做出.于是笔者进行如下设置.

(Ⅰ)请过BD中点作出二面角A-BD-C的平面角，并说明理由；

(Ⅱ)分别确定△ABD，△BCD的外接圆圆心O1,O2位置；

(Ⅲ)作出三棱锥A—BCD的外接球球心O，并说明理由；

(Ⅳ)求出三棱锥A—BCD的外接球半径.

【命题意图】进行这样的原创设置，不仅充分展现了题目的逐层递进，而且更让学生在由浅入深，轻松的氛围中掌握知识.在能力层面上，培养了学生空间想象能力和数据处理能力以及应用意识.在知识层面上，考查了二面角的平面角定义，三棱锥的外接球含义.

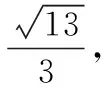
【点评】本题是在任何教辅资料、各省模拟题、高考真题中都不会出现的，如果直接用【原创例题3】进行教学，虽然考查的内容一样，但是对难点、重点突破不了.而【原创例题4】能通过四问完美的突破难点、重点，而且让学生真正掌握这一类题型的通法.

三、及时引导和纠正学生错误的思维过程

由于学生的思维不受课堂的制约，所以课堂教学设疑和提问的过程中，往往会出现意想不到的回答，但是正是这样的回答恰好体现了学生思维过程的真实性.如果不能加以合理的引导和纠正，这种思维将会在学生脑海中根深蒂固.而此时需要教师的原创试题来“对症下药”，从而更好地引导和纠正这种错误的思维过程.如：在讲授函数零点解答题时，学生由于受到小题数形结合的影响，常常用数形结合思想求解零点问题，为了引导和纠正这一问题，笔者命制了如下原创例题.

【原创例题5】已知函数f(x)=ex-2x-a(a∈R).

(Ⅰ)求函数f(x)的单调性；

(Ⅱ)讨论函数f(x)零点个数.

【分析】(Ⅰ)略解：f(x)在(-∞,ln2)上单调递减，在(ln2,+∞)上单调递增.

(Ⅱ)由于受到小题数形结合的影响，在学生中出现一种不规范的解答：

因为函数f(x)的零点个数即为方程ex-2x-a=0的实根个数，

即表示函数g(x)=ex-2x与y=a的交点个数，

由(Ⅰ)可知f(x)在(-∞,ln2)上单调递减，在(ln2,+∞)上单调递增，

且g(x)min=2-2ln2，如图所示.

当a<2(1-ln2)时，函数f(x)在R上无零点；当a=2(1-ln2)时，函数f(x)在R上有1个零点；当a>2(1-ln2)时，函数f(x)在R上有2个零点.

【点评】此题第二问，乍一看学生的解法，好像无懈可击，其实此解法极其不规范，因为学生是用函数的性质去画函数的图象，此时得到函数的图象本身就是不严谨的，而又用函数的图象去解决函数的有关性质问题，这就更不规范.在高考中作为解答题是要被扣很多分的.

【正解】因为函数f(x)的零点个数即为函数图象与x轴交点的个数，

由(Ⅰ)可知f(x)在(-∞,ln2)上单调递减，在(ln2,+∞)上单调递增，

且f(x)min=2-2ln2-a，

当a<2(1-ln2)时，f(x)>0恒成立，此时函数f(x)在R上无零点；

当a=2(1-ln2)时，f(x)≥0恒成立，当且仅当x=ln2时取得等号.

此时函数f(x)在R上有1个零点；

当a>2(1-ln2)>0时，则f(ln2)<0，

所以函数f(x)在(-∞,ln2)上有且只有1个零点；

又因为f[ln(3a+2)]=eln(3a+2)-2ln(3a+2)-a=2[a+1-ln(3a+2)]，

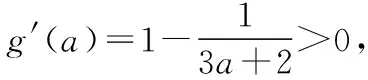
所以g(a)>g(0)=1-ln2>0，所以f[ln(3a+2)]>0，又因为ln(3a+2)>ln2，

即可得f(ln2)·f[ln(3a+2)]<0，又因为f(x)在(ln2,+∞)上单调递增，

所以此时函数f(x)在(ln2,+∞)上有且只有1个零点；

故函数f(x)在R上有2个零点.

综上所述,当a<2(1-ln2)时，函数f(x)在R上无零点；当a=2(1-ln2)时，函数f(x)在R上有1个零点；当a>2(1-ln2)时，函数f(x)在R上有2个零点.

【点评】此解法完全符合高考标准答案的解法，完全纠正学生做任何题都想采用数形结合思想进行解题的套路，同时引导学生做解答题时，解题过程一定要规范.

当笔者认为此题应该告一段落时，在课下有个学生找到我，就此题提出了一些疑问：如果是客观题时，用数形结合思想进行解题非常简便，但是怎么就能确定函数的图象在无限趋近-∞和+∞时，函数的图象就一定趋近+∞呢？有没有可能趋近某个特定的值呢？有没有这样的例题呢？就学生提出的这些疑问笔者在第二天的课堂上讲解了如下原创例题.

【原创例题6】已知函数g(x)=2x+mex(m∈R)存在两个不同零点，则m的取值范围是________.

【命题意图】主要考查学生的数形结合思想、数据处理能力、转化与化归思想.同时在知识上主要是考查函数零点、函数图象等问题.

【分析】作为客观题，可以进行如下思考：

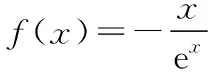
其实答案是错的，原因是当x趋近于+∞时，g(x)趋近于0，即函数的图象为下图：

【点评】通过此题的讲解，能很大程度上引导学生解题时要有严谨的态度.

四、提升学生分析问题和解决问题的能力

一线教师常常热衷于数学例题的讲解、解答示范和解题训练，但是教学效果往往出现低效现象——“听得懂、想不到”的状况，其原因在于学生没有抓住或者深入挖掘此题的本质.而教师讲解其个人命制的试题时，更容易让学生理解命题意图和题目本质.教学中充分结合学生的认知规律，设置不同梯度原创题，由具体到抽象，由易到难，形成知识的迁移，不断提升分析和解决问题的能力.如：教师想让学生掌握二次函数型函数零点问题，设置如下原创巩固练习题.

【原创例题7】已知函数g(x)=8e(lnx)2-(2e+8)x|lnx|，f(x)=-2x2，则方程g(x)-f(x)=0的实根个数是________.

【分析】由方程g(x)-f(x)=0，学生很显然能得到8e(lnx)2-(2e+8)x|lnx|+2x2=0，而对方程根的判断，学生首先会想到能不能直接解方程，如果能解又该如何解呢？学生掌握的是一元一次方程、一元二次方程、指数方程、对数方程等解法，而对如此复杂的方程，又该如何解呢？那么此时学生就会思考原方程是不是可以进行变形转化等，一步一步把学生推向正解的“彼岸”.

【原创例题8】已知函数g(x)=4e(lnx)2-(2em+4)x|lnx|+2mx2，则函数g(x)有5个不同的零点，则实数m的取值范围是________.

【命题思路】重点考查学生数形结合思想，转化与化归思想，培养学生分析问题和解决问题的能力.在知识层面上，更好地体现函数图象、函数零点的实际应用.

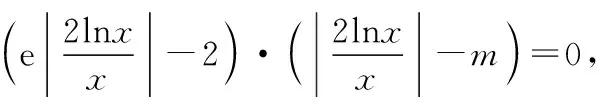
【点评】此题是在【原创例题7】的基础上进行命制，充分展现了由易到难，形成知识的迁移，不断地提升分析和解决问题的能力，同时进一步巩固知识.也进一步说明只要真正理解题目的本质，就能解决这一类型的题目，达到例题的真正典型作用.

五、有利于教师及时了解学生的学习情况和提升个人教学、解题的能力

教师给自己教授的学生命制试题时应更注重巩固目的、激励目的和反馈目的.这样才有利于帮助学生正确认识自我，有利于教师及时了解学生的学习情况，以便决定教学的起点与进度，决定教学内容的深度与广度.有利于教师改进教法，提高教学水平，进而提高教学质量．同时教师在命制原创题时，都是经过“选择命题点—磨题—做题—修改—再磨题”的过程，而这个过程更是提升教师本人教学、解题能力的过程，只有不断把这个过程延续下去，才能成为一名优秀的教师.