一类趋化-流体耦合方程组的能量不等式
何 璞,林静秋
(西华大学理学院,四川 成都 610039)
1 预备知识
趋化方程是一类刻画细胞自我组织和趋化运动规律的数学模型,这类问题经典的研究模型是标准Keller-Segel模型[1],标准Keller-Segel模型的解的整体存在性和有限时刻爆破等问题已经被大量数学工作者研究(参考综述[2-4]及其中的参考文献)。然而,在实际生物学背景中,细胞所处流体环境对于细胞趋化运动行为同样有着不可忽视的影响。因而,文献[5]的作者经过实验观察,提出了如下趋化-流体(chemotaxis-fluid)耦合模型:

此处的未知函数n=n(x,t)表示细胞密度、c=c(x,t)代表化学物质、信号的浓度,u=u(x,t)和P分别表示流体速度场和相应的压力;参数κ∈R与非线性流体对流项的强度有关;φ表示重力势,是已知函数。
本文将考虑这类方程组的如下初边值问题:
(1)
其中,Ω⊂RN为具有光滑边界的有界凸区域。这类方程组研究的一个基本问题是解的整体存在性和有界性,而能量不等式估计的方法是研究方程(组)解的整体存在性与有界性的一个重要方法。一旦建立了方程组的能量不等式,我们就可结合Lp-Lq估计、Neaumann热半群、Stokes半群的衰减性质等建立方程组解的相应先验估计;从而最终建立方程组解的整体存在性或有界性。本文将主要建立方程组(1)的一个能量不等式。
(2)

本文的主要结果为下述能量不等式。
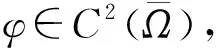
(3)
2 主要结果的证明
下面开始定理1的证明。
定理1的证明: 证明分几步完成。
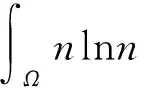
显然,直接求导可得

对上式右边第二项进行分部积分易得
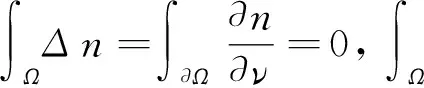
也就是:
(4)
另一方面,方程组(1)中第一个方程两端同时乘以lnn再在Ω上积分得

对上式左边第二项进行分部积分得
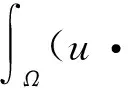
类似地,直接计算得

也就是:
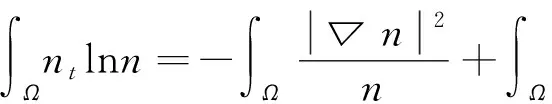
(5)
结合上面式(4)、(5),得到:
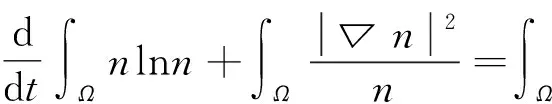
(6)

直接微分,并将ct=Δc-nc-u·▽c代入计算得到:
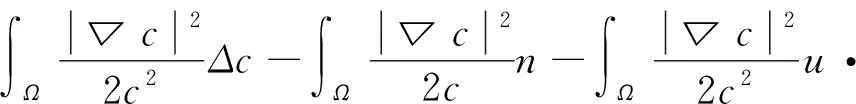
(7)
下面对式(7)右边各积分项进行估计。

(8)


(9)
其中:

(10)
将式(10)代回到式(9),得到

(11)
再将式(11)代入式(8),得到
移项整理后,得到
(12)
又因为
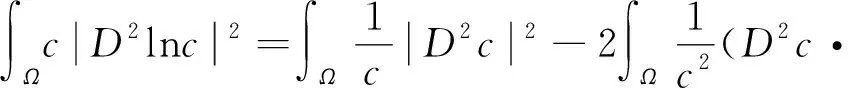
其中:
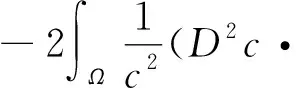
所以

(13)
将式(13)代人式(12)得
(14)
结合式(7)和式(14),可得
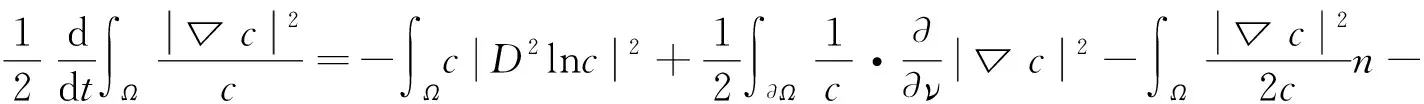
(15)
对上式右端最后一项进行分部积分可得
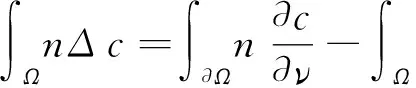
代入(15)式得到
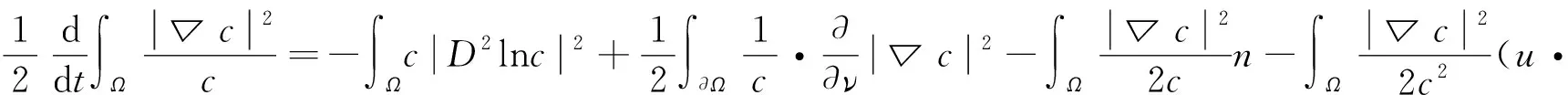
(16)
结合式(6)和式(16)可得
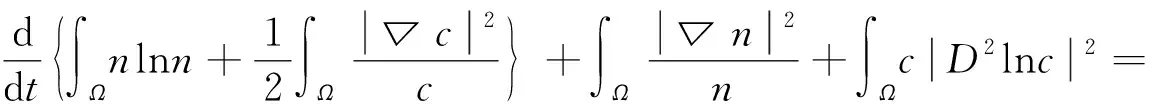
(17)
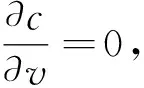
因而,由式(17)得到
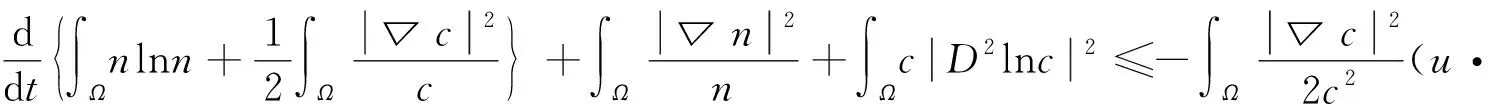
(18)
3)对不等式(18)右端进行估计。


为了运算方便,我们不妨令:
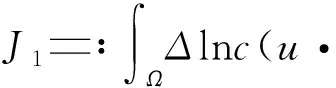
利用Young不等式可得
再对J2进行估计
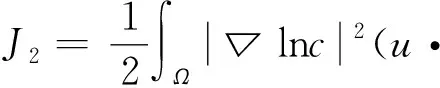
进一步,利用Young不等式估计J2,
由三角不等式,我们有
(19)
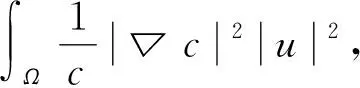
(20)


(21)
由Hölder不等式得:
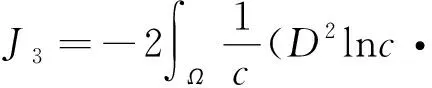
整理J3和J4,代回到式(21)得
(22)
将式(22)代入式(20),得到
(23)
再将式(23)代入到式(19),得到
(24)
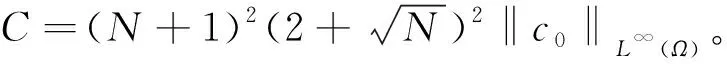
从而最终得到能量不等式
(25)
3 结论
能量估计方法是偏微分方程研究中的一种常用方法,常常被用于偏微分方程解的整体存在性及有界性证明。本文建立了一类趋化-流体耦合方程组的能量不等式,既为此类方程组解的有界性的证明奠定了基础,也为更为复杂的模型的能量不等式研究提供了一个方法基础。

