基于GARCH-EVT模型VaR法的开放式基金风险测度研究

程建华 丁慧敏

（安徽大学，安徽 合肥 230601）

大量实践表明，基金行业是高风险行业，如果不能有效地控制和规避金融风险，会带来极为严重的损失。1994年奥兰治县破产案、1995年巴林银行倒闭实践及2008年全球金融危机的发生，究其根源无疑均是风险控制系统的失衡。在基金行业中，科学有效的风险管理机制是基金公司实现良好收益的重要条件，精准的风险估计不仅有助于基金管理者选择合适的投资策略，也为投资者选择合适的基金产品提供了一项重要参考指标。从一定程度来说，基金行业的竞争其实就是控制风险能力强弱的竞争，因此风险度量在基金行业内具有重要意义。

我国的基金行业相比于西方发达国家起步较晚，运作经验不足，开放式基金市场投机性强、流动性弱、波动频繁，与开放式基金运作的理想环境相差较远。因此，建立合理的风险评价体系对我国开放式基金的发展意义重大。

我国开放式基金面临风险复杂多样，从宏观角度看，法律政策、金融措施以及经济周期的变化都可能会对开放式基金的运作产生影响；从微观角度看，证券市场走势、基金资产流动性、基金经理的投资策略等也会造成开放式基金运作的波动，引发风险。1993年G30会议报告中，首次明确提出利用VaR度量与控制市场风险。VaR是指在一定概率水平下，资产组合在未来一段时间可能遭受的最大损失。这种简单且直观的风险描述方法能够将复杂的风险因素归一化，正适用于我国的开放式基金风险度量。

本文研究的主要问题有：

（1）针对我国开放式基金波动特征，采用何种模型进行拟合；

（2）在极端市场条件下，VaR方法能否准确测度风险；

（3）如果VaR方法无法有效度量极端条件下的基金风险，该采用何种方法解决。

为解决上述问题，本文的研究思路为：现有研究表明GARCH模型能较好的拟合金融时间序列的高峰厚尾与波动集聚的特征，为此本文建立GARCHVaR模型；考虑到序列在极端市场中的波动情况，引入极值理论（EVT）对模型的尾部进行拟合，构建GARCH-EVT-VaR模型；最后，对上述两种模型以易方达50指数为样本进行实证分析，比较二者实证结果。

一、文献综述

虽然风险管理相比于其他的学科是一门年轻的学科，但是风险研究从未间断过。1952年Markowitz建立方差均值模型，来量化风险和收益[1]。1964年，其学生William F.Sharpe在此基础上，提出资本资产定价模型（CAPM）[2]。1976年，针对CAPM模型具有不可检验的缺点，Stephen Ross提出一种可代替的资本资产定价模型，即套利定价理论（APT）[3]。这些研究成果为金融风险研究打开了量化分析的大门，人们可以对资产组合进行量化分析与评估。Markowitz[1]与William F.Sharpe[2]因为他们在金融风险量化理论的巨大贡献成为了1990年诺贝尔经济学奖的获得者。

1993年G30会议报告中，首次提出了VaR这一概念。1994年，JP.Morgan公司在其年报中披露的该公司一天的概率水平为95%的VaR值为1,500万美元，其含义为针对1994年该公司的资产组合，如果确定一个时间点，从这一时间点看，在未来一天内的资产损失值有95%的可能性不高于1,500万美元。可以看出，VaR方法能够将复杂的风险因素归一化，简单且直观地描述风险。

在进行VaR风险估计时，大部分学者都以金融时间序列数据服从正态分布与同方差作为前提假设，然而大量实证研究表明，金融时间序列的分布具有高峰厚尾与异方差特征，并不符合正态分布与同方差假设。为了描述金融时间序列特有的波动特征，1982年，RobertF.Engle提出自回归条件异方差模型（ARCH），该模型将当期一切可利用信息作为条件，并利用前期扰动项的平方刻画条件方差的波动，运用ARCH模型，能够刻画出随时间而变异的条件方差[4]。1986年，Bollerslev将ARCH模型拓展到广义自回归条件异方差模型（GARCH），解决了ARCH模型拟合阶数过大的问题[5]。杨夫立（2012）基于GARCH模型，研究了基金日收益率时间序列在正态、t、GED三种不同分布下的VaR方法，利用Kupiec失败频率检验方法检验模型的准确性，同样发现扰动项在GED分布假设下计算的VaR值更加准确[6]。相比于杨夫立[6]的研究，于孝建等（2018）采用了包含日内收益率、日收益率的混频数据，在正态分布、t分布及GED分布三种扰动项假设下，对GARCH、Realized GARCH和M-Realized GARCH三种模型的VaR预测效果进行比较，认为M-Realized GARCH模型预测精度最高[7]。

杨夫立[6]与于孝建[7]都针对GARCH模型扰动项的三种假定进行实证分析，比较不同扰动项假定对风险度量结果的影响，后者比前者多比较了两种GARCH拓展模型，但本质都是基于GARCH模型，没有考虑到对模型进行灵敏度以及参数估计方法的改进。谢合亮（2017）在利用传统蒙特卡洛法计算VaR值时，不仅引入了GARCH模型解决指数收益的高峰厚尾特征及波动集聚特征，还利用马尔可夫链对GARCH模型的参数进行估计，弥补了传统蒙特卡洛方法在高纬度和静态方面的缺陷[8]。江涛（2010）分别利用GARCH-VaR法与半参数VaR法对上证综合指数的日收益率序列计算其相应的VaR值，证明了半参数VaR法相较与GARCH-VaR法预测精度更高[9]。上述VaR度量方法都是在市场正常情况，那么必须要考虑两个问题，一是这些方法在遇到极端事件时是否仍然使用；二是如果不适用，该如何解决。

Dimitris N.Dimitrakopoulos（2010）进一步对新兴市场和发达市场股票组合的市场风险量化问题进行研究，评估并比较了传统VaR方法在正常、危机和危机后三段时期的应用，研究表明，传统VaR方法在正常时期能较准确地预测，但在极端时期，预测效果一般[10]。那么，该如何解决VaR方法在极端情况下产生的偏差，并提高金融风险度量的准确性呢？Abhay K.Singh（2013）将单变量极值理论应用于ASX-ALL普通（Australian）指数及S&P-500(USA)指数的极端市场风险建模并发现EVT能够成功的应用于金融市场收益序列[11]。 David E.Allen（2013）等以 FTSE 100 英国指数和标准普尔500美国市场指数为样本，比较了多种计算VaR的方法，从GARCH及其变体的已知计量经济学模型到专门关注分布尾部的基于EVT的VaR模型，实证结果表明EVT可以成功的运用于金融市场收益序列[12]。 Madhusudan Karmakar（2013）利用极值理论（EVT）对印度股市尾部相关风险测度进行估计，采用了McNeil和Frey(2000)提出的两阶段条件EVT方法来估计动态风险值(VaR)和预期缺口(ES)，对不同百分位数的回报进行风险度量，发现在不同分位数水平下计算的风险度量估计值在所选阈值范围内表现出很强的稳定性，这意味着基于分位数的估计风险度量的准确性和可靠性[13]。在金融市场中，极端价格变动与正常时期的市场修正相对应，也对应于股票市场崩溃、债券市场崩溃或非常时期的外汇危机，而基于极值理论计算VaR正是考虑到了市场中的极端情况。

此外，很多学者将极值理论与其他方法相结合，以期对拟合效果进行优化，王传好等（2016）运用多分辨率分析（multi-resolution analysis,MRA）将收益率时间序列分解成不同时域上的正交分量，利用极值理论（EVT）分析收益率的厚尾性特征，MRA-EVT模型能够明显提高VaR的预测精度[14]。傅强等依据金融市场中某金融资产不同风险的非线性及非对称尾部的特征，利用极值理论和Copula函数估计条件VaR值，对深证成指进行实证研究，结果显示EVT能够很好地拟合收益率的尾部[15]。

当然，也不乏一些学者比较极值理论与其他方法度量VaR的准确度，如陈坚（2014）运用Copula方法和极值理论构建VaR模型，比较两种方法下VaR的预测能力，研究发现基于极值理论的VaR模型预估能力较好，而基于Copula法的VaR模型预测效果一般[16]。Ramazan Gencay（2001）等将极值理论与其他方法在股票市场中计算VaR值的准确度进行了比较，其研究的模型可以分为两大类，一类为GARCH族模型，另一类由历史模拟、Var-CoV法、自适应广义帕累托分布及非自适应广义帕累托分布组成，研究发现GPD模型预测稳定性更高[17]。

近年来，大多数学者对风险的考察较为片面，杨夫立[6]与于孝建[7]对于金融时间序列的风险度量都是基于金融市场正常条件下，并未考虑极端条件下的风险度量。Dimitris N.Dimitrakopoulos[10]指出传统的VaR方法在极端情况下的风险估计精度较低，Abhay K.Singh[11]与Madhusudan Karmakar[13]引入极值理论对金融时间序列尾部进行拟合，但是忽略了金融时间序列的高峰厚厚尾与波动集聚的特征，仍是基于序列服从正态分布及同方差的假设。作者认为EVT法与GARCH模型的侧重点不同，前者侧重描述分布的尾部，而后者侧重分布的整体波动情况，因此，本文创新性地提出基于GARCH-EVT的VaR方法，该方法的优点表现在以下几个方面：（1）VaR的概念易理解，为风险管理者提供了一种统一的方法预估风险，是一种很好的风险控制的量化工具。（2）GARCH模型能够实时跟踪波动的变化，后期的波动率由前期的波动率来预测，在整个时期内波动率都是变化的，能够很好的拟合波动。（3）极值理论在解决极端事件方面具有显著的优越性，它并不假设金融收益的尾部特征，而根据理论计算得出尾部形状参数，此时相较传统VaR方法，极值理论能更好的估计风险。

二、模型的理论框架

（一）GARCH-VaR 模型

VaR为“处于风险中的价值”，是指市场正常波动情况下，某一金融资产或证券组合的可能遭受的最大损失。更确切说，在一定概率水平下（置信度），在未来特定的一段时间内，某一金融资产或证券组合的可能遭受的最大损失。表示为：

其中，△P为证券组合在持有期△t内的损失；VaR为置信水平c下处于风险中的价值。

针对金融时间序列高峰厚尾的波动特征，Bollersev（1986）基于ARCH模型提出了广义自回归条件异方差模型 （Generalized Autoregressive Conditional Hetero skedasticity Model)，即 GARCH模型。

假设在 ARCH（q）过程 εt=σtvt中，vt～i.i.d.N(0,1),t=1,2,…,T。令ARCH过程的阶数q→∞，条件方差可以表示为

其中π（B）为无穷阶滞后多项式：

其中，滞后项1-β(B)的特征方程的根均在单位圆外，则可利用上式将σt2改写成：

其中 α0=(1-β1-β2-…-βp)×ω，则由（6）式定义的 ARCH过程 εt=σtvt称为 GARCH 过程，记为 εt～ GARCH(p,q)。

其中 p≥0，q≥0，α0＞0，α1≥0 （i=1，2…，q)，β1≥0 （i=1，2，…,p）；β（B）为滞后算子多项式且 β（B）=β1B+β2B2+…+βpBp。

若利用GARCH模型进行估计VaR，首先要假定扰动项εt的分布，本文假定扰动项的分布是正态分布，对所选金融时间序列进行拟合，生成相应的条件方差σt2和条件均值μt，则时刻t的VaR表达式为：

其中，F-1（α）为扰动项在正态分布假定下置信水平为α的分位数。

（二）GARCH-EVT-VaR 模型

GARCH-EVT模型不同于GARCH模型，它并不对序列扰动项设置任何假定，而是运用广义帕累托分布（GPD）进行拟合，广义帕累托分布函数含有两个参数：

其中，β＞0，当 ζ≥0 时，x≥0；而当 ζ＜0 时，0≤x≤-β/ζ。ζ是重要的形状参数，而β是分布的尺度参数。

Pickands-Balkama-de Haan定理[22]中阐述道，用u表示一个充分大阈值，令超过阈值u的样本个数为Nu，用 X1,…，XNu表示超过阈值的样本观测值，用 Y1，…，YNu表示相应超额数，即 Yi=Xi-u,i=1,2,…,Nu。令 x0表示分布F的右端点，它可能是有限的，也可能是无限的，即 x0=sup｛ x∈R；F（x）＜1｝≤∞。 令X的超额数的分布函数为

其中，0≤y≤x0-u。若F属于Hζ的最大吸引场，那么广义帕累托分布是超额数分布的极限分布，该结论以如下定理的形式给出。

定理 对每一个 ζ∈R，F∈MDA（Hζ），当且仅当对某个正的测量函数β(u)，

定理表明，对足够大的阈值u，超额数的分布函数可以用广义帕累托分布Gζ,β（x）近似。 故可对超额数用广义帕累托模型进行拟合。

根据式（8）和（9），若 x＞u,则

这里的目标是根据式（10）构造。为此，需要：1）找到足够大的阈值 u，2）估计广义帕累托分布 Gζ,β（x-u）的参数ζ、β；3）估计 F(u)。 获取到阈值 u、广义帕累托分布 Gζ,β（x-u）的参数 ζ、β 以及 F(u)后，将所有估计量带入式（10）中，得到 F(x)的尾部估计

注意，这个估计量只对尾部x＞u有效。

若给定概率q＞F(u),则反解式（11）能计算q分位数的估计：

时间序列在t时刻的一步预测分位数用表示，由的条件分布知

所以

其中，Zq表示扰动项Zt的上侧q分位数。

为了估计xtq，需要选择一种特定的模型描述时间序列的条件期望及条件波动性。于孝建等[10]提出GARCH模型能够较好的拟合金融序列的波动特征，故利用GARCH模型计算条件期望和条件方差。

基于GARCH-EVT模型的VaR估计方法可通过以下三步实现：第一步，用GARCH模型模拟负对数回报（Xt），对扰动项的分布不做任何假定。用伪极大似然法估计模型参数，再利用拟合的模型估算条件期望和条件方差，并用zt=(xt-μ^t)/σ^t计算标准残差。第二步，将zt看作是扰动向的一个样本实现，它是独立同分布的。用GPD分布估计zt分布的尾部，由式（14）得到极值分位数 zq的估计（其中 q＞F(u)）。第三步，结合条件均值、条件方差以及极值分位数计算GARCH-EVT-VaR估计值，即在置信水平为q的条件下，VaRq估计值表达式如下：

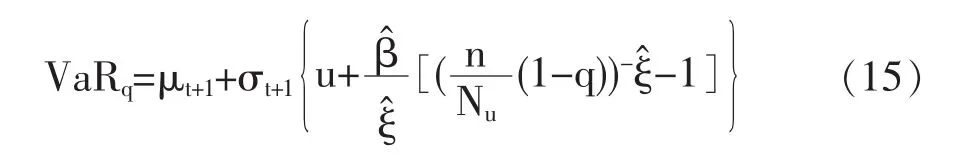
（三）Kupiec检验

假定计算VaR的置信度是c，实际考察天数是T，失败天数是N，则失败频率为p（N/T）。原假设为p=p*。这样对VaR模型准确性的检验就转化成检验失败频率p是否显著不同于p*。

由二项式过程得到N次失败在T个样本中的发生概率为：(1-p)T-NpN。Kupiec提出了对原假设p=p*最适合的检验时似然比率检验：

LR=-2ln［(1-p*)T-Np*N］+2ln［(1-N/T)T-N(N/T)N］p*（16）在原假设的条件下，统计量LR服从自由度为1的卡方分布。

三、实证分析

（一）样本选择及研究区间的确定

本文选取2004年3月22日成立的契约型开放式基金——易方达50指数证券投资基金为样本，研究GARCH-EVT-VaR模型的应用，并与GARCHVaR模型比较，采用的数据为样本基金的每日单位净值，数据来源于中国基金网。

研究区间为2009年7月28日～2018年4月23日，共2101个交易日。基金的日收益率为Rt=ln(NATt/NATt-1)，其中NATt为基金第t日的单位净值，令Xt=-Rt，得到2100个指数条件损失值。选择2009年7月28日～2015年9月23日的指数条件损失数据用于建模分析、数值计算；选择2015年9月24日～2018年4月23日的指数条件损失数据用于Kupiec的失败频率检验。

（二）数据特征分析

首先，绘制基金的指数条件损失直方图（图1），可以看出基金日指数条件损失序列右侧有较长的拖尾，序列可能具有高峰厚尾的波动特征。故对序列作进一步的描述性分析见表1，基金日指数条件损失序列的偏度约为0.354,4，即分布为右偏；基金日指数条件损失序列的峰度约为6.551,0，大于正态分布的峰度3，为尖峰分布，说明这些基金有高峰厚尾的波动特征。JB统计量为819.519,2，则易方达50指数日指数条件损失分布在1%的显著水平下拒绝正态分布的假设。

表1 描述性分析

图1 易方达50指数条件损失直方图

检验样本基金的指数条件损失序列的平稳性，ADF值为-37.94,814，在0.01的显著性水平下，基金的指数条件损失序列均拒绝存在一个单位根的原假设，说明样本基金的指数条件损失序列平稳。由样本自相关函数值和偏自相关函数值以及Q检验统计量（见表2），根据伴随概率，在显著性水平0.05下，直到6阶显著拒绝无自相关性的零假设，这种高阶自相关性反映了序列的波动集聚性，基金的指数条件损失序列进行ARCH-LM检验，LM统计量值为2.457,934，其伴随概率为0.022,8，说明易方达50指数的指数条件损失序列的误差项εt｛｝均存在高阶ARCH效应，故可对误差项εt进行进一步的建模分析。

表2 自相关检验统计结果

（三）基于GARCH模型计算VaR值

由上，易方达50指数条件损失时间序列平稳，且无自相关性，则其均值方程中不含滞后项。由AIC值为-7.108,916且SIC值为-7.101,828，初步认为GARCH(1，1)可以较好的拟合数据。假定扰动项服从正态分布，运用GARCH(1,1)模型，对易方达50指数条件损失序列进行拟合，拟合结果为：

从模型的估计结果看，除均值方程的常数项外，模型的其他参数均在5%置信水平下显著，再对估计残差做LM检验，发现不存在显著的异方差性，则GARCH（1，1）模型能够较好的拟合损失序列变化。依据GARCH模型拟合结果，代表新信息对市场波动影响的残差项平方的系数为0.045,2，代表旧信息对市场波动影响的条件方差项的系数为0.944,5，后者的系数远大于前者，说明旧信息对市场波动的影响远大于新信息。两项的系数之和为0.989,7小于1但非常接近1，说明基金的波动具有持久性，所以基金过去的波动对其未来走势有重要影响。

表3 各概率水平分位数

（四）基于GARCH-EVT模型计算VaR值

利用GARCH模型拟合指数条件损失Xt，对扰动项的分布不做任何假定，利用伪极大似然方法求出条件方差标准差 σt、条件均值 μt。 根据 zt=(xt-μt)/σt计算模型的标准化残差，绘制标准化残差序列直方图（图2），由图 2可以看出分布的左侧有较长的拖尾，而图形的最高点约为220，标准化残差序列可能具有高峰厚尾特征，对标准化残差进行描述性分析见表4。

表4 描述性分析

图2 标准化残差直方图

标准化残差序列偏度小于零，即分布为左偏；峰度大于3，为尖峰分布，该序列具有高峰厚尾特征；根据JB统计量，易方达50指数日指数条件损失分布在1%的显著水平下不服从正态分布。对标准化残差序列进行平稳性检验，ADF值为-37.992,71，说明样本基金的日收益率平稳。由于样本自相关函数值和偏自相关函数值以及Q检验统计量，标准化残差序列zt不存在自相关性，再对易方达50指数的标准化残差序列zt｛｝进行ARCH-LM检验，LM统计量值为0.758,513，其伴随概率为0.602,6，说明标准化残差序列zt｛｝不存在高阶ARCH效应，故认为zt｛｝具有i.i.d特征，因此可以利用EVT法对分布的尾部建模。

首先，绘制标准化残差均值超额图（图3），由图3可知，在1＜u＜2时，图形近似一条直线，在u＞1.8时，样本点数目过少，可能导致方差过大；1983年DuMouche研究发现，在u允许的条件下选取10%左右的数据用作极值理论尾部估计较为合适，极值数据组的样本量过多或过少均可能导致样本拟合不足与过度，故本文选取u=1.72作为估计VaR的阈值，则F(u)的经验估计为0.96。因此，对于q＞0.96的分位数进行广义帕累托估计。

图3 易方达50指数标准化残差均值超额图

求得参数ξ、β的估计值，其中形状参数ξ=-0.134,1，尺度参数β=0.819,0。根据阈值u及参数ξ、β，分别计算出概率水平为 0.975、0.99、0.995、0.999 的标准化残差序列的分位数zq，见表5，最后利用GARCHEVT模型的VaR表达式（15）分别计算出在不同概率水平下的VaR值。

根据阈值u=1.72，利用似然函数：

表5 各概率水平分位数

（五）Kupiec回测检验结果及分析

利用2015年9月 24日～2018年 4月23日的600个收益率数据，运用Kupiec失败频率检验法检验VaR模型的准确性，Kupiec检验方法在实际使用时，首先将估计的风险值与实际的损失值比较,如果风险值小于实际损失值，就认为风险值估计失败。根据VaR定义知,若显著性水平为5%，将100天的估计VaR值与实际损失值比较，在这100天内，实际损失只超过估计VaR值的次数应该是次。若实际损失值大于估计VaR值的次数远高于5次，认为该模型估计的VaR值不准确，即表明相应的风险测度模型不合适。回测结果如表6所示。

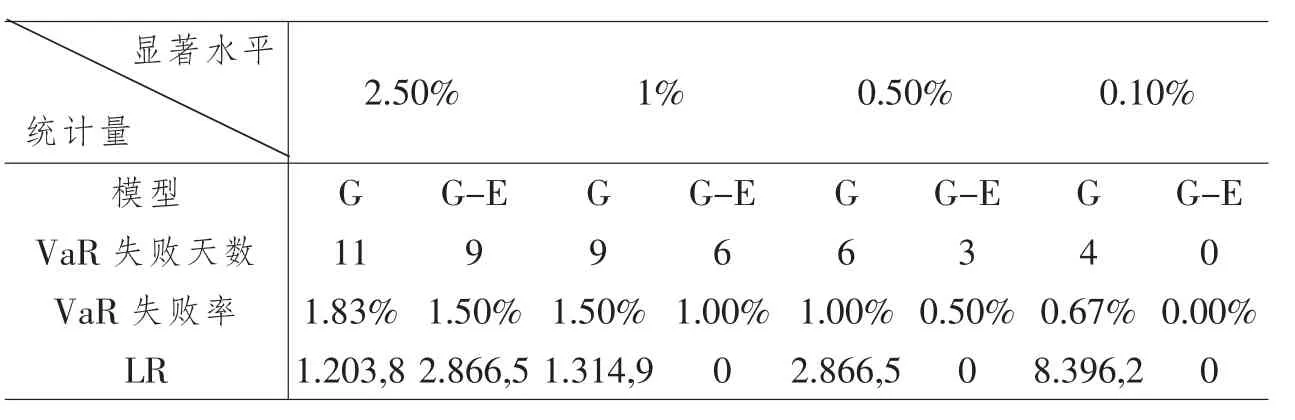
表6 GARCH模型与GARCH-EVT模型回测结果

由表6可知，在失败天数方面，基于GARCH模型的VaR估计的失败天数均大于基于GARCH-EVT模型的VaR估计。从失败率看，在2.5%、1%、0.5%、0.1%四个显著水平下，基于GARCH模型的VaR估计仅在显著水平为2.50%时，VaR的失败频率落在Kupiec失败频率检验的非拒绝域内，其余均不能通过Kupiec失败频率检验；而基于GARCH-EVT模型的VaR估计的失败频率都落在Kupiec失败频率检验的非拒绝域内，均通过Kupiec失败频率检验。最后，从LR统计量看，基于GARCH模型的VaR估计LR统计量的值随着显著水平的降低逐渐增大，说明GARCH模型对尾部的拟合偏差正逐渐增大；基于GARCH-EVT模型的VaR估计LR统计量的值随着显著水平的降低逐渐减小，说明GARCH-EVT能够较好的拟合分布的尾部。

结合LR统计量与失败频率，可以看出GARCH模型明显低估基金风险，而GARCH-EVT模型较好估计了风险。因此，本文认为利用基于GARCH-EVT的VaR混合方法估计不仅是有效的，而且能够很好的进行基金风险评估。

四、总结与展望

本文以开放式基金易方达50指数为研究对象，根据金融时间序列具有波动集聚与高峰厚尾的特征，将GARCH模型与极值理论纳入到VaR的框架中，构建GARCH-EVT-VaR模型，并分别利用该模型与GARCH-VaR模型对易方达50指数进行实证分析，并对两种方法的计算结果进行Kupiec回测检验，结合LR统计量以及失败频率的分析，得出以下结论：

（1）GARCH-VaR模型计算的VaR值低估了易方达50指数的市场风险，而GARCH-EVT-VaR模型以指数条件损失未来可能上升的最大值描述了市场风险，说明GARCH-VaR模型忽视极端情况造成了风险的低估，而极值理论的引入解决了极端事件中模型拟合的偏差。因此，认为GARCH模型与EVT的配合使用能较好地刻画基金市场风险。

（2）基金的波动具有持续性，且前期的波动对当期的波动有较大影响，具体反映在式（13）中ARCH项系数为0.045,2，GARCH项系数为0.944,5，后者系数远大于前者，而两系数之和为0.989,7小于1但接近1。因此，在对基金损失率建模分析时，基金的持续性不容忽视。

此外需要说明的是，本文使用的数据为2009年7月28日～2018年4月23日的日损失率数据，由于基金市场的更新速度快，使用日内高频率数据分析可能会得出其他有用的结论。