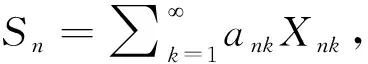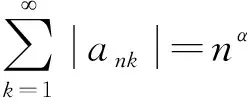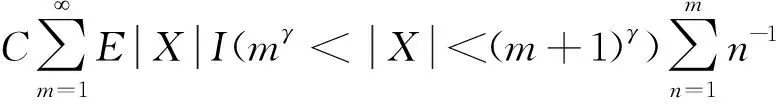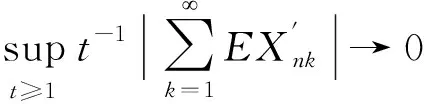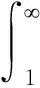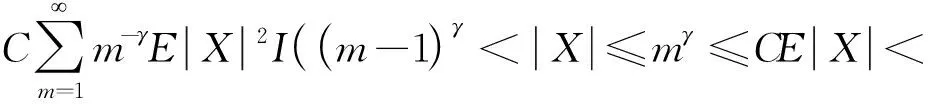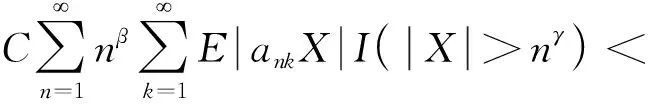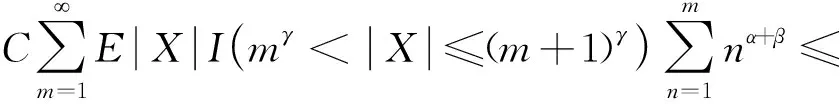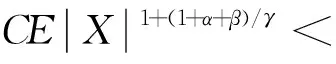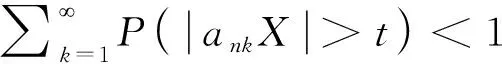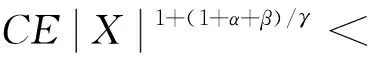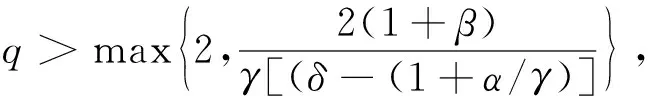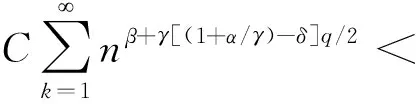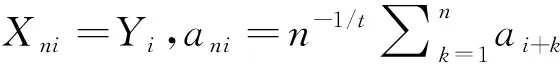负相关随机变量加权和的矩完全收敛性*
戴泽兴,吕文华
(滁州学院 数学与金融学院,安徽 滁州 239000)
0 引 言
负相关(NA)随机变量序列的概念最早起源于文献[1]。
定义1 定义一组随机变量序列{Xk,1≤k≤n},若对于{1,2,…,n}任意的非空不相交的子集A、B以及任意的实值非减函数定义在RA上的f和RB上的g,均有
Cov(f(Xi,i∈A),g(Yj,j∈B))≤0
成立,则称随机变量Xi是负相关序列。
众所周知,NA序列是一种包含独立随机变量,范围非常广的序列。目前为止,NA序列已经被大量应用于可靠性理论、多元统计分析和渗透理论中。自JOAG-DEV 和PROSCHAN F[1]发现NA序列以来,很多专家学者都先后研究了NA序列的收敛性,SU[2]发现了NA序列在风险管理中的重要作用,GAN和CHEN[3]给出了NA序列最大部分和的极限形式,CHEN和SUNG[4]研究了NA序列加权和的一种条件矩完全收敛性,WU和WANG[5]给出了一个NA随机变量序列的非参数回归模型估计的完全相合性的结果。涉及NA序列的极限理论方面,越来越多的专家学者做了大量的研究,包括KOMH[6],SHAO[7],CAI[8],KUCZMASZEWSKA[9],WU[10],SU[11],YANG[12],WU[13],WU[14],ZHAO[15]。然而,极少有文献研究NA序列的加权和的矩完全收敛性,以下正是基于此目的做出的研究。
如果对于任意的ε>0,存在a,使得:

则称序列{Un,n∈N}是完全矩收敛的。
这个概念第1次是由HSU和ROBBINS[16]提出的,根据Borel-Cantelli引理,上面的结果意味着Un→a几乎处处成立。因此,完全收敛性在证明随机变量和和随机变量的加权以及几乎处处收敛成立时是一个非常重要的工具。
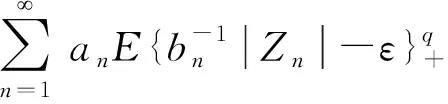
如果存在常数C使得:
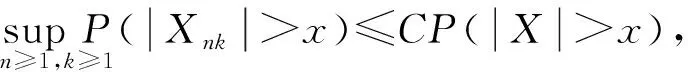
则称随机变量序列{Xnk,k∈N,n∈N}是由随机变量X随机分配的(记为{Xnk} BAEK[18]研究了NA序列加权和的完全收敛性得到了下面的定理。 定理1 设β≥-1,{Xnk,k≥1,n≥1}为一列NA随机变量,对于所有的n,i和x≥0,EXnk=0,P(|Xnk|>x)≤CP(|X|>x)成立,令{ank,k≥1,n≥1}为一常数序列,则: (1) (2) 若1+α+β>0,存在δ>0使得α/γ+1<δ≤2, E|X|v<,其中则对所有的 ε>0: (3) 若1+α+β=0,E(|X|log(1+|X|))<,则式(3)成立。 BAEK[18]还从定理1中推导出了NA序列移动平均过程的完全收敛性。 定理2 设{Yi,- (2) 令1 (3) 若E(|Y|log(1+|Y|)<,对任意的ε>0: 将改进定理1和定理2,在相同条件下,得到更强的完全矩收敛的结论,这是完全收敛更为一般的情形(见注1)。 本文中符号C代表正常数,I(A)代表示性函数。 首先引入一些证明过程中用到的引理。 引理1[1]定义在非空不相交的负相关随机变量上的非减函数也是负相关的。 引理2[7]令{Xk,k≥1}是一列NA随机变量序列,对于q≥2,k≥1,有EXk=0,E|Xk|q<,存在C=C(q),对所有的n≥1: 引理3 设{Xnk,k∈N,n∈N}是一列{Xnk} (1)E|Xnk|qI(|Xnk|≤x)≤ C{E|X|qI(|X|≤x)+xqP(|X|>x)} (2)E|Xnk|qI(|Xnk|>x)≤CE|X|qI(|X|>x) 这个定理很容易通过分部积分证得,此处省略过程。 假设Φ:[-b,b]→R是满足下面条件的函数 (1)Φ在a处有界且连续; (2) 存在δ>0,C>0,对于所有的|x|≤δ,|Φ(x)|≤C|x|。 接下来给出主要结果,证明过程将在下一部分给出。 定理3 设β≥-1,{Xnk,k∈N,n∈N}是一列EXnk=0,{Xnk} (1) 若1+α+β=0,E(|X|log(1+|X|))<,则对所有的ε>0: (4) (2) 若1+α+β>0,存在δ>0使得α/γ+1<δ≤2,E|X|v<,其中式(4)成立。 注1 定理3的条件同定理1的条件: 定理3改进了定理1。 后面将给出一个从定理1改进到定理3的线性过程完全矩收敛的实例。 定理4 设{Yi,- (1) 令β>-1,1≤t<2,若E|Y|(β+2)t<,对于任意的ε>0: (2) 令1 (3) 若E(|Y|log(1+|Y|)<,对任意的ε>0: (5) (6) 对于给定的ε>0,有: 根据定理1,可直接得到I1<,接下来证明:I2<,令 (ankXnk-t)I(ankXnk>t) 为了证明式(4)成立,需要证明I3<和I4<,将分以下两种情况讨论: (1) 1+α+β=0 先证明I3<,注意到: 由于α+β=-1,根据引理3,式(5)和式(6),得到: CE(|X|log(1+|X|))< 因此,为了证明式(4),只需证明I4<成立,先证明当n→时: (7) 根据EXnk=0和引理3,可得,当n→时: Cn-(1+β)E|X|I(|X|>nγ)→0 因此,当n充分大时: (8) 当t≥1时,根据式(8)和引理2,可得: 对于I7,可以用证明I3<的结论,同理证得: 对于I6, CE|ankX|I(|ankX|>1) 令t=u,用证明I3<的结论,同理证得: 对于I5,有 用证明I3<的结论,同理可证得 到此,1+α+β=0的情况证明完毕。 (2) 1+α+β>0 由引理1,可知v≥1和v>1+α/γ,当n→时: Cnα-(v-1)γE|X|vI(|X|>nγ)→0 因此,式(7)仍然是正确的。选择参数q,令 根据马尔可夫不等式和引理1,可得: 类似定理3(1)中证明I4<的方法(用q替代指数2),可证得I8<,由引理2和q>2,可得: 注意到,当n→时: Cnα-(v-1)γE|X|vI(|X|>nγ)→0 若δ<2,根据 证毕。 对i≥1,n≥1,则: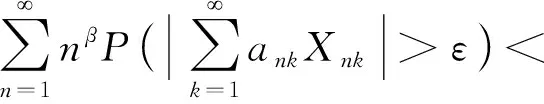
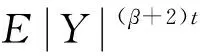

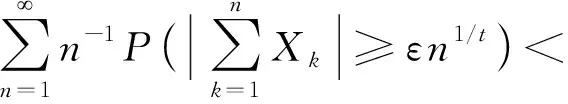

1 预备知识及主要结论
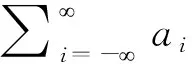


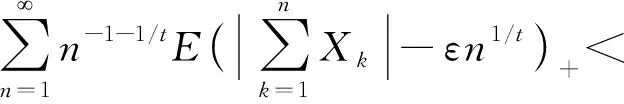
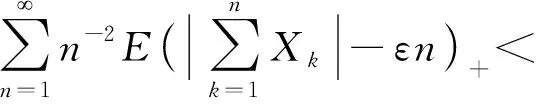
2 证明过程