On Log-concavity of a Generalized Fibonomials Sequence∗

SUN Yi

(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract: In recent years,log-concavity and log-convexity of combinatorial sequences have aroused great interest of many scholars in the feild of c o mbinatorics.We consider in this note that log-concavity of a combinatorial sequence called s-Fibonomial sequenceWe confrim that the sequence is log-concave with respect to k and also demonstrate that it is neither log-concave nor log-convex with respect to n.However,when s is even we prove that the s-Fibonomial sequence is log-concave with respect to n.Moreover,by considering the parity of n−k,we also establish two inequalities on s-Fibonomial sequence.

Key words:Fibonacci numbers;s-Fibonomials sequence;log-concavity;log-convexity

0 Introduction

Denote by N and the interval[a,b]the set of natural numbers{0,1,2,···}and the set of{a,a+1,···,b},respectively,where bothaandbare integers anda≤b.

LetFn(n∈N)denote thenth Fibonacci number,which satisfies the following recurrence relation

and the initial valuesF0=0,F1=1.It is well known that

Throughout this work,we letsdenote a positive integer.

For a given Fibonacci numberFn,thes−Fibonacci factorial ofFn,written as(Fn!)s,is defined as(Fn!)s=FnsF(n−1)s···F2sFs.Givenn∈ P andk∈ N,thes-Fibonomials are also calleds-Fibonomial coefficientswhich are defined byand

that is

According to the definition ofs-Fibonomials,it is clear to see thatBy applying the Binet formula(1),it is not difficult to obtain the identity

Based on the identity(3),the following recurrence fors-Fibonomials is obvious,

which can be used to show thats-Fibonomials are integers by a simple induction argument,see[1].

It seems thats-Fibonomials first occured in 1967 in the paper[1]by Hoggatt Afterwards,Gould[2]studied some properties of divisibility and congruences.Recently,Pita did quantities of research ons-Fibonacci sequenceFnsand the correspondings-Fibonomials and obtained many fruitful results,see[3].Evidently,thes-Fibonomials degenerate to general Fibonomials whens=1.For more information on Fibonomials,we refer readers to[4,5].For combinatorial interpretations of Fibonomials,see[6–8].However,a combinatorial interpretation ofs-Fibonomials is still unknown.

Recall that a sequence of non-negative integers{ak}0≤k≤nis called log-concave if

It is easy to show that this is equivalent to the seemingly stronger condition

for allk,landisatisfying 0≤k≤l≤nand 0≤i≤k−l.In recent years,due to the relationship with real zeros of polynomials and problems of unimodality,proving that various sequences are log-concave has been a topic of increasing interest,see surveys[9,10].Given a set of non-negative integerstn,kdefined forn∈N andk∈[0,n],we say thattn,kis log-concave inkif for any fixednthe sequences{tn,k}0≤k≤nis log-concave,i.e.,tn,ksatisfies the following inequalityBesides,we calltn,kis log-convex inkif for any fixednthe sequences{tn,k}0≤k≤nsatisfy the following inequality

Moreover,letkbe fixed,we can define log-concave innsimilarly.

The present paper aims to show thats-Fibonomials is log-concave with respect tok.Its proof is given in the second part.In the third part,we shall consider whether or not thes-Fibonomials is log-concave innwhenkis given.We also put forward several interesting open problems in the forth part.

1 Log-concavity of s-Fibonomials in k

Before proving the main result of this note,we need the following lemma,

Lemma 1Lets,n,k∈N such that 0≤k≤n.The following inequality holds,

ProofSinces∈N,by the recurrence of Fibonacci numbers and the original conditions,it follows easily thatFks≤F(k+1)sandF(n−k)s≤F(n−k+1)s.Thus the inequality(7)holds by multiplying the above two inequalities.

Theorem 1For fixedn∈N andk∈[0,n],the sequenceis log-concave.

ProofFor the sake of convenience,letfn,kdenote thekths-Fibonomial coefficient,i.e.,By the definition of log-concave sequence and the inequality(5),it suffices to show that

Note that the inequality(8)is equivalent to It follows from Lemma 1.We are done.

As an application of Theorem 1,we have that

Corollary 1Thes-Fibonomial sequenceis unimodal.

2 Log-concavity of s-Fibonomials in n

2.1 Special examples

For the sake of brevity,we first give some examples in the following tables.

Table1 for s=1

Table2 for s=2

Table3 for s=3

Based on the table below,it seems that the following examples can give us some hints on the log-concavity ofs-Fibonomial sequence.

Lettings=1,take table 1 for example,the numberequals toFn.Note thatF1F3>F22 andF1F4>F2F3,So it is not a log-concave sequence in this settings.But we have that

Lettings=2,see table 2,by simple calculating,it is not difficult to obtain that

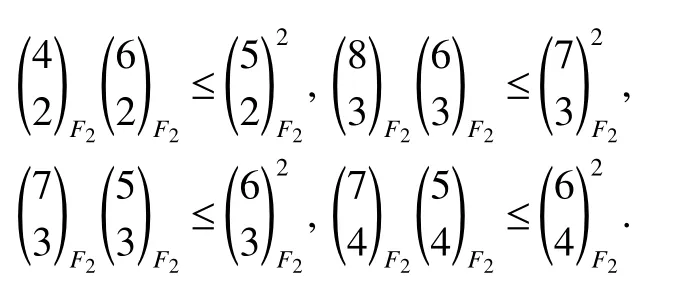
Lettings=3,see table 3,we have

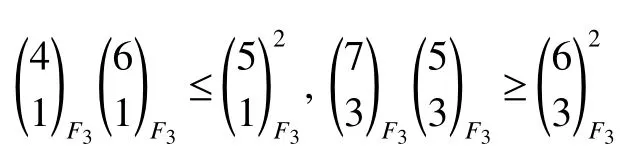
and

These examples show thats-Fibonomial sequence is not bound to be a log-concave sequence with respect to the variablenwhenkis given.It is a natural question occur to us what conditions should be satisfied to make the sequence log-concave with respect ton.The following part shall give the answer.

2.2 Log-concavity of s-Fibonomials in n

Though thes-Fibonomial sequence is not log-concave for any integernwhenkis given,it has the log-concavity whensis even.

Theorem 2Given nonnegative integerkand even positive integers,then thes-Fibonomial sequenceis log-concave.

ProofWhensis even,to demonstrate log-concavity of the sequenceis equivalent to show that

Note that

By the formula(1)and αβ=−1,it follows that

This completes the proof.

By(10),we see that

According to(11),the following results are obvious.

Theorem 3Given nonnegative integerskandsin the set of positive integers,there hold the following inequalities,

3 Final Remark and Further Direction

We adopt the algebraic method to study log-concavity property ofs-Fibonomials in this note.As a matter of fact,we know that there always exists an injective(resp.,surjective)proof of a log-concave(resp.,log-convex)sequence.Unfortunately,we are unable to find an injective proof of log-concavity ofs-Fibonomials as a result of no combinatorial interpretation ofs-Fibonomials known to us.So it is still an open problem to find a combinatorial interpretation ofs-Fibonomials.Whens=1,s-Fibonomials reduce to ordinary Fibonomials,which has several combinatorial interpretations[6–8].It is interesting to give an injective proof of Corollary 2.