Conditional Lie-B¨acklund Symmetry and New Variable Separation Solutions of the Third Order KdV-Type Equations∗
Gai-Zhu Qu(屈改珠), Shun-Li Zhang(张顺利),Hai-Xia Li(李海侠),and Gang-Wei Wang(王岗伟)
1School of Mathematics and Physics,Weinan Normal University,Weinan 714000,China
2Center for Nonlinear Studies,School of Mathematics,Northwest University,Xi’an 710069,China
3Institute of Mathematics Science,Baoji University of Arts and Sciences,Baoji 721013,China
4School of Mathematics and Statistics,Hebei University of Economics and Business,Shijiazhuang 050061,China
AbstractThe functionally generalized variable separation solutions of a general KdV-type equations ut=uxxx+A(u,ux)uxx+B(u,ux)are investigated by developing the conditional Lie-B¨acklund symmetry method.A complete classification of the considered equations,which admit multi-dimensional invariant subspaces governed by higher-order conditional Lie-B¨acklund symmetries,is presented.As a result,several concrete examples are provided to construct functionally generalized variable separation solutions of some resulting equations.
Key words:KdV-type equation,conditional Lie-B¨acklund symmetry,invariant subspace,functionally generalized separation solutions,dynamical system
1 Introduction
Constructing possible explicit solutions to a nonlinear evolution equations(NLEEs)arising from the field of mathematical physics is a popular topic.There are various approaches used to deal with NLEEs,some of the commonly used ways involve the Lie point symmetry method,[1−3]the nonclassical method,[4]the Clarkson-Kruskal(CK)direct method,[5−7]the conditional Lie-B¨acklund symmetry(CLBS)method,[8−14]the signinvariant method,[15]and the invariant subspace(IS)method.[16−22]Focusing on the symmetry of the conservative infinite-dimensional dynamic systems,Bridges et al.proposed the multi-symplectic method,[23]which has been generalized to the damping dynamic system by Hu et al.[24]Of these methods,the CLBS method has been a highlight,which can be regarded as a natural generalization of the nonclassical symmetry method.Therefore the procedure of computing CLBS is similar to that of the nonclassical symmetry.Furthermore,CLBS method can also be applied to study exact solutions defined on invariant subspace(IS)for nonlinear evolution equations or their invariant forms,and the functional separable solutions or the derivative-dependent functional separable solutions were obtained.[11−14]
In the present paper,we use the CLBS method to study the general KdV-type equations

where u(x,t)denote the unknown functions of the space variable x and time t,A(u,ux)and B(u,ux)are smooth functions of their arguments to be determined later.
Equtaion(1)includes a lot of important nonlinear equations as its special cases.Such as the famous KdV equation

the modified KdV equation

the STO equation

and so on.
In what follows,we recall some definitions and theorems that we use in the paper.Consider a k-th order nonlinear evolution equation

Let V be an evolutionary vector field with the characteristic η,

Here we use the following notations

Definition 1The evolutionary vector field(3)is said to be a Lie-B¨acklund symmetry of Eq.(2)if and only if

where L is the set of all differential consequences of the equation ut−E=0,that is

Definition 2The evolutionary vector field(3)is said to be a CLBS of Eq.(2)if and only if

where M stands for the set of all differential consequences of the equation η=0 with respect to x,that is=0,j=0,1,2,....
Proposition 1Equation(2)admits the CLBS(3)if there exists a function W(t,x,u,η)such that

According to Proposition 1,Eq.(2)admits the CLBS(3)with the characteristic

For Eq.(1),we set the characteristic


admits CLBS

In fact,Eq.(1)and Eq.(6)are related by the following transformations:

Proposition 2Equation(6)admits the CLBS with the characteristic(7)if and only if

where the prime denotes the Fr´echet derivative and

It follows from Proposition 2 that Eq.(6)is right the invariance condition of the subspace

with respect to the operator E,where Wlis the solution space of l-th order linear ordinary differential equation η =vlx+al−1(x)v(l−1)x+ ···+a0(x)v.
Notice that E[Wl]⊆Wl,namely,

Thus we can conclude that if Eq.(6)admits CLBS(7),then Eq.(6)possesses the generalized separable solution

where{Ci(t)}satisfy the l-dimensional dynamical system

using the invariant condition(11),one can obtain the maximal dimension of the invariant subspaces preserved by E,and it is given by the following theorem.
Theorem 1If a linear subspace Wlis invariant under a nonlinear ordinary differential operator E of order k,then

The main purpose of this paper is to develop the CLBS method for dealing with classification and exact solutions to Eq.(1).The remainder of this paper is organized as follows.In Sec.2,we perform the classification on Eq.(6)admitting CLBSs(7)and the corresponding ISs(13).In Sec.3,the FGSSs of some examples in the resulting equations are obtained.Finally,we summarize our findings and give some remarks in Sec.4.
2 Equation(6)and Its CLBS(7)
For the third-order differential operator E,according to Theorem 1,we know that the dimension of invariant subspaces cannot exceed 7,therefore we will consider the following cases for l=3,4,5,6,7.
First,we discuss the case of l=3.By using the symbolic computation software Maple from Eq.(11),a straightforward calculation leads to


where the primes and the subscripts denote the derivatives and the partial derivatives with respect to the indicated variables respectively.And the right-hand side of Eq.(17)is a polynomial of vxx,which must vanish identically.The coefficients of vandyield the following overdetermined system:

Solving this system,we obtain all the classifying equations and CLBSs collected in Table 1,where riand hereafter denote arbitrary constants.The unknown functions are given in the following:

When l=4,5,6,7,and after similar calculations,we can derive Eq.(6)and the corresponding CLBSs(7)presented in Table 2.
In Table 2,the unknown functions are given as below:



Table 1 CLBSs(7)and ISs(13)with l=3 of Eq.(6).

Table 2 CLBSs(7)and ISs(13)of Eq.(6)with l=4,5,6,7.

Table 2(continued)
3 Some Reductions and FGSSs of Eqs.(1)and(6)
In this section,we seek for the FGSSs for Eqs.(1)and and(6).For convenience,we just set out several examples to illustrate this approach.
Example 1The equation

The corresponding solutions are given as follows:
(i)For r1>0,the solution defined on the invariant subspaceis given by

where C1(t), C2(t), and C3(t) satisfy the threedimensional dynamical system:

(ii)For r1<0,the solution defined on the invariant subspaceis given by
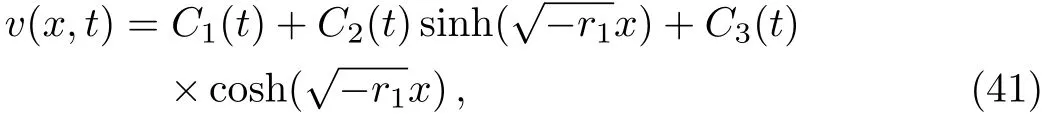
where C1(t), C2(t), and C3(t)satisfy the threedimensional dynamical system:

By the proper transformation v=g(u),we can obtain the corresponding FGSS of the equation

In particular,we consider the KdV equation with source

it possesses the exact solution

then the dynamical system becomes

These exact periodic solution admits a soliton-traveling wave representation,namely,

Letting C2(t)=0 and C1(t)=C3(t),we can derive the solution on W{cos2[(1/2)(x−t)]}given by

where T>0 is the finite time.Then the following equation

has the blow-up soliton-type solution.
Example 2The equation

admits the CLBS

The corresponding solution defined on the invariant subspace W{1,x,x2,x3}is given by

where C1(t),C2(t),C3(t),and C4(t)satisfy the threedimensional dynamical system:

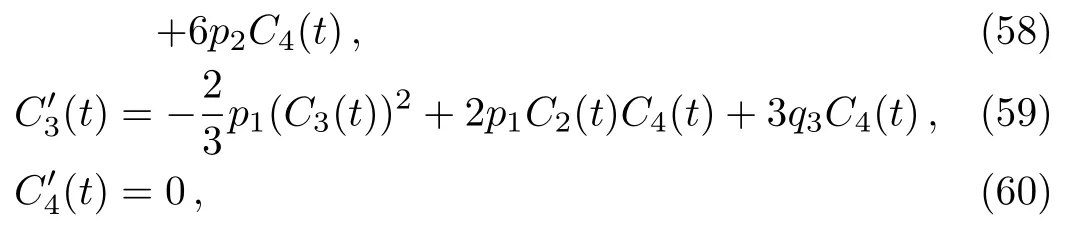
solving the above system,we have the one exact solution

and the other solution

By the appropriate transformation v=g(u),we can obtain the corresponding functionally generalized variable separation solution of the equation

4 Conclusions
In the current paper,by applying the CLBS and the IS method,we have discussed the FGSSs for the general KdV-type equations.A complete classification of invariant forms for those equations which admit the corresponding higher-order CLBSs with ISs is displayed.And some FGSSs of the considered equations are constructed.However,it is of interest to develop the CLBS method with IS to construct the FGSSs of higher-dimensional nonlinear equations and their version of with discrete case,which will be considered in our future work.
 Communications in Theoretical Physics2018年10期
Communications in Theoretical Physics2018年10期
- Communications in Theoretical Physics的其它文章
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking∗
- Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations∗
- Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
- Pair Production in Chromoelectric Field with Back Reaction∗
- Baryogenesis in f(R,T)Gravity∗
