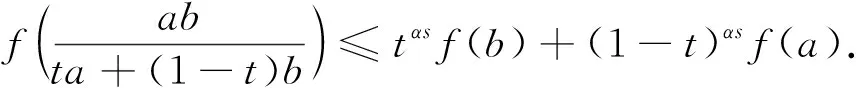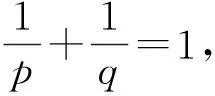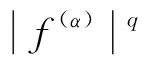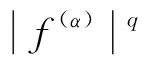分形集上的广义调和s-凸函数及Hadamard型不等式
孙 文 兵
(邵阳学院 理学院, 湖南 邵阳 422000)
1 引言与预备知识
很多不等式的研究都与函数凸性有关, 例如Hermite-Hadamard不等式: 令f:I⊆→是一个凸函数, 其中a,b∈I,a (1) 如果f是凹的, 则不等式号相反. 目前, 关于Hermite-Hadamard型不等式的研究已取得了许多成果[1-14]. 定义1[9]令I⊂(0,∞)是一个区间. 如果对所有的x,y∈I,t∈[0,1]以及某一固定的s∈(0,1], 均有 (2) 则称函数f:I→是一个调和s-凸(凹)函数. 定理1[9]令f:I⊂(0,∞)→是一个调和s-凸函数,a,b∈I,a (3) 定义2[14]令I⊂{0}是一个区间. 对所有的x,y∈I,t∈[0,1], 均有 (4) 则称f:I→α(0<α≤1)是一个分形集上的广义调和凸函数. 如果不等式反号, 则f是一个分形集上的广义调和凹函数. 本文基于分形集理论及局部分数阶微积分理论[15-16], 给出分形集上广义调和s-凸函数的定义及其相关性质, 建立广义调和s-凸函数推广的Hermite-Hadamard不等式以及分形空间上其他与局部分数阶积分有关的Hermite-Hadamard型不等式. 1)aα+bα∈α,aαbα∈α; 2)aα+bα=bα+aα=(a+b)α=(b+a)α; 3)aα+(bα+cα)=(a+b)α+cα; 4)aαbα=bαaα=(ab)α=(ba)α; 5)aα(bαcα)=(aαbα)cα; 6)aα(bα+cα)=aαbα+aαcα; 7)aα+0α=0α+aα=aα且aα1α=1αaα=aα. 定义3[17]若对所有的u,v∈+(+=[0,∞)), 均有 其中λ1,λ2≥0,λ1+λ2=1, 则称函数f:+→α为第二种意义下的广义s-凸函数(0 引理1[15]1) 若f(x)=g(α)(x)∈Cα[a,b], 则 2) 若f(x),g(x)∈Dα[a,b], 且f(α)(x),g(α)(x)∈Cα[a,b], 则 引理2[15] 定义4令函数f:I⊂(0,∞)→α(0<α≤1). 如果对所有的x,y∈I,t∈[0,1]及某一固定的s∈(0,1], 均有 (5) 则称f是一个广义调和s-凸函数. 如果式(5)中不等号反号, 则称f是广义调和s-凹函数. 性质1如果f:I⊂(0,∞)→α是一个广义s-凸函数且不减的, 则f是一个广义调和s-凸函数. 证明: 对于x,y∈(0,∞)且t∈[0,1], 易证 因为f: (0,∞)→α是一个广义s-凸函数且不减的, 则 因此f是一个广义调和s-凸函数. 性质2如果f:I⊂(0,∞)→α是一个广义调和s-凸函数且不增的, 则f是一个广义s-凸函数. 证明: 对于x,y∈(0,∞)且t∈[0,1], 易证 因为f: (0,∞)→α是一个广义调和s-凸函数且不增的, 则 由定义3知,f是广义s-凸函数. 例1令0 如果bα≥0α且0α≤cα≤aα, 则f是广义s-凸函数(第二种意义下), 且f在区间(0,∞)上是不减的[17]. 根据性质1,f是广义调和s-凸函数. 定理2(广义调和s-凸函数的Hermite-Hadamard不等式) 令f:I⊂(0,∞)→α是分形空间上的一个广义调和s-凸函数, 且a,b∈I,a (6) 证明: 因为f:I⊂(0,∞)→α是一个广义调和s-凸函数, 在式(5)中取则对所有的x,y∈I, 均有 (7) 将式(7)两边对t在[0,1]上局部分数阶积分, 由引理2和引理4, 可得 因此 (8) 另一方面, 注意到f是一个广义调和s-凸函数, 对t∈[0,1], 有 (9) (10) 将式(9),(10)相加, 可得 (11) 将式(11)两边对t在[0,1]上局部分数阶积分, 由引理2可得 (12) 其中 证毕. 注1在定理2中, 取α=1, 则由不等式(6)可得不等式(3). 下面给出分形空间上的两个特殊函数: 1) Beta函数 2) 超几何函数 引理5令I⊂{0}是一个区间,f:I°⊂{0}→α(I°是I的内部)使得f∈Dα(I°), 且f(α)∈Cα(a,b),a,b∈I°,a 证明: 设 由局部分数阶分部积分, 可得 换元 可得 证毕. 定理3令I⊂(0,∞)是一个区间,f:I°→α(I°是I的内部)使得f∈Dα(I°), 且f(α)∈Cα[a,b],a,b∈I°,a 其中: 计算可得 类似地, 有 由式(15)~(19), 可得不等式(14). 证毕. 注2在定理3中, 取α=1, 可得文献[10]中定理8. 定理4令I⊂(0,∞)是一个区间,f:I°→α使得f∈Dα(I°), 且f(α)∈Cα[a,b],a,b∈I°,a 证明: 设At=ta+(1-t)b. 对式(13)两边取模, 由引理3可得 计算可得 由引理2, 可得 (25) 因此, 结合式(21)~(25)可得结论. 证毕. 注3在不等式(20)中, 若取α=1, 则通过简单计算可得文献[10]中定理9.
2 主要结果