动态规划算法的教学探讨

陈晓梅 张晶

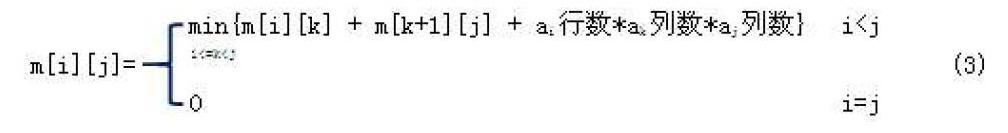
摘要：在动态规划算法的教学中，学生最迷惑的是递归公式的建立与“翻译”。并不以单一个具体的事例来讨论动态规划算法的实现，而是利用若干个各具代表性的实例来抽象出动态规划算法的共性以及解题方法。

关键词：动态规划；递归公式；备忘录；自底向上

中图分类号：O221.3 文献标识码：A 文章编号：1009-3044（2018）26-0146-02

1 概述

有一类问题，可以将待求解的问题分解成若干子问题，先求解子问题的解，然后通过这些子问题的解来求得原问题的解。若分解的子问题出现重叠，如果使用常规的递归方法来设计算法，则会耗费大量时间重复计算相同的子问题。而动态规划使用备忘录或自底向上的方法来设计算法，以保证每个子问题最多只被计算一次。

本文基于动态规划求解问题的共性思维探讨动态规划算法的教学过程。

2 动态规划算法案例选择

在动态规划算法的教学中，可以选择一些经典的、代表性强的案例进行教学。使用动态规划解决问题，关键是要确定某个状态的最优解，因此状态的选择是否正确，决定整个问题求解的正确性。一般可选择以第i时刻为起点、第j时刻为终点的状态，如矩阵连乘问题。还可以选择以最小规模子问题或原问题规模为起点、第i时刻为终点的状态，如最长公共子序列问题、最大子段和问题和0-1背包问题。

3 动态规划算法求解问题

动态规划一般用于解最优化问题。利用某个状态（一般是初始状态或目标状态）的最优解去计算下一个状态的最优解，直至获得原问题的全局最优解。因此，使用动态规划求解问题的一般步骤是：分析该问题是否满足动态规划求解的条件；建立递归公式表示某个状态的最优值；使用备忘录或自底向上的方法计算最优值；构造最优解（有需要的话）。

3.1 分析问题

3.1.1 最优子结构性质

当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质[1]。动态规划算法求解问题时，正是通过利用子问题的最优解来计算原问题的最优解，因此要求该问题要满足最优子结构性质。满足最优子结构性质的问题，其子问题一定是相互独立的。

可以使用反证+剪贴[2]来证明最优子结构性质。有原问题Q，其最优解为S，若该问题不满足最优子结构性质，即S中所包含的子问题Q1的解T并非Q1的最优解。不妨设T是Q1的最优解，从原问题的最优解S中将T剪下来，将T贴上去，若子问题相互独立，将会获得原问题Q的另一个解S=S-T+T，由于T优于T，故S优于S，此结论与S是原问题的最优解矛盾。因此假设不成立。T就是子问题Q的最优解。即原问题满足最优子结构性质。

在最优子结构证明的教学中，需要提醒学生注意子问题的提取方式。其必须是在原问题假设的一个最优解中提取出来，而不是原问题中的任意一个子问题。如：假设矩阵连乘问题的最优解的首层断点是矩阵k，即optimal（[a1：an]） = optimal（[a1：ak]）+optimal（[ak+1：an]）+a1行數*ak列数*an列数，则由此产生的子问题是[a1：ak]和[ak+1：an]，应由这两个子问题出发去证明最优子结构性质。

3.1.2 重叠子问题性质

重叠子问题是指在计算不同的子问题的最优解时，这些不相同的子问题产生了相同的子子问题，这会导致有些子问题会被重复计算。

可以列出一个规模比较小的实例，对该实例逐层分解子问题，以判断是否有重叠子问题性质。如假设矩阵连乘问题的一个实例是[a1：a4]，则原问题可能产生的子问题是：[a1：a1]、[a2：a4]、[a1：a2]、[a3：a4]、[a1：a3]、[a4：a4]，而子问题[a2：a4]会产生[a2：a2]、[a3：a4]、[a2：a3]、[a4：a4]，显然[a3：a4]出现重复计算现象。随着矩阵连乘问题规模的加大，重叠子问题的数量会迅速增加，达到指数级别[1]。

动态规划算法使用备忘录或自底向上的方法计算每一个子问题的最优值，从而保证每个子问题最多只被计算一次。

3.2 建立递归公式

在这一步，将会使用数学公式来表示子问题的最优解。由于动态规划算法总是通过利用子问题的最优解来计算原问题的最优解，因此当计算某个子问题时，又会产生对更小规模的子问题的求解，该过程可以使用递归来描述。在教学过程中，可以从子问题的表示、求解子问题的递归公式，以及原问题的表示三个步骤递进分析。其中关键步骤是子问题的表示，以下基于子问题表示来展开探讨。

要表示一个子问题，就要分析表示该子问题所需的维度及每个维度的含义，这可以对应理解为表示这个子问题的参数个数及每个参数的含义。无论是什么问题，其中一个共同的参数必定是这个子问题的范围，而其他参数则与具体问题相关。

3.2.1 子问题的范围

有些问题，其产生的子问题的起点或终点都相同且与原问题的起点或终点一致，其子问题的范围可用一个维度表示。如在求a1..an的最大子段和问题中，最大子段有可能以任一个元素ai为结尾。因此需要计算所有以ai（1<=i<=n）为结尾的最大子段和Ti，max{Ti}即为全局最优值。这些子问题（求a1..ai中以ai为结尾的最大子段和）范围的起点相同且与原问题一致（起点都是a1）。同时这些子问题的求解不受其他因素约束，故可将子问题表示为c[i]，其含义是a1..ai中以ai为结尾的最大子段和。进一步分析，c[i]依赖于c[i-1]，故可用c[i-1]来计算c[i]。相应递归公式如公式（1）所示。原问题最优值表示为max{c[i]|1<=i<=n}。

另一角度分析，c[i]亦可理解为以ai为起点的ai..an最大子段和，这种表示可看作子问题的终点相同且与原问题一致（终点都是an），此时c[i]依赖于c[i+1]。相应递归公式如公式（2）所示。原问题最优值可表示为max{c[i]|1<=i<=n}。

满足以上特点的可用动态规划求解的典型问题还有很多，如最长单调递增子序列问题，最长公共子序列问题，编辑距离问题，游艇租用问题，0-1背包问题，等等，这些问题都可以使用上述思路写出递归公式。

有些问题，其产生的子问题的起点或终点不相同，其子问题的范围需要使两个维度表示。如矩阵连乘问题[a1：an]，其首层子问题是[a1：ak]和[ak+1：an]（1<=k

3.2.2 子问题的其他约束条件

有些问题，其子问题的表示还受其他条件的约束，这就需要把这些约束条件加入到子问题的数学表示中。如0-1背包问题，其子问题范围可用i标记，表示当前可选物品是第1件到第i件物品，或第i件到第n件物品。0-1背包问题的最优解还受当前背包剩余容量的约束，因此子问题的最优值应记为m[i][j]，表示在前述物品范围内，当前背包容量为j的情况下的最优价值。相应递归公式如公式（4）（5）所示。原问题的最优值是m[n][C]（根据公式（4））或m[1][C]（根据公式（5））。

3.3 数据结构与算法选择

动态规划算法使用备忘录或自底向上的方法计算每一个子问题的最优值，从而保证每个子问题最多只被计算一次。无论是备忘录方法还是自底向上方法，其关键实现都是一张表格，表格的维度与子问题维度相同，表格中每个维度的大小与子问题对应参数的取值范围一致。在C++中可使用数组表示。表格中的每一项对应一个子问题。如最大子段和问题，其子问题最优值表示为c[i]，显然表格设置为一维数组a即可，根据公式（1），a[i]的值表示序列中以第i个数为结尾的最大子段和；又如0-1背包问题，其子问题最优值表示為c[i][j]，可将表格设置为二维数组a，根据公式（4），a[i][j]的值表示当前背包容量为j，待选物品是第1件到第i件状态下的最优价值。

在使用递归方式“翻译”递归公式时，以上面所述的表格充当备忘录。先将备忘录中的每一项初始化为一个特殊的值，每次求解子问题时，先到备忘录查看该子问题是否已记录答案，若有，直接返回答案，否则，递归求解计算该子问题并把答案写入备忘录。

若使用自底向上方式“翻译”递归公式，其实质就是“填表”。填表范围、从表格的哪一项开始填以及按照什么顺序继续填，是有规律可循的。从子问题表示的每个维度的取值范围，可确定填表范围；从递推公式和原问题的表示方式，可确定从表格的哪一项开始填以及按照什么顺序继续填。如矩阵连乘问题，根据公式（3），1<=i<=j<=n， 显然这是一张n行n列的二维表a，填表范围是右上三角（含对角线）；原问题的最优值是m[1][n]，对应表格右上角a[1][n]；递推公式表明，在计算第i行第j列的最优值a[i][j]时，需要利用a[i][i：j-1]以及a[i+1：j][j]的值，即要先求出表格中a[i][j]的左边部分以及下面部分的值。因此，首先应填右下角a[n][n]的值，然后按照自下而上，自左向右的顺序来填表格a的右上三角，最后填的是a[1][n]，即原问题的最优值。

4 结束语

动态规划算法是一种比较抽象的算法，在动态规划教学中，需要向学生讲清楚理论分析和递归公式的建立。本文着重从求解问题的共性思维出发，介绍了具体的理论分析方法以及操作性强的建立和“翻译”递归公式方法。实践证明，学生利用该思路能够较好地解决一些动态规划典型问题。

参考文献：

[1] 王晓东. 计算机算法设计与分析.第4版[M]. 电子工业出版社， 2012.

[2] ThomasH.Cormen. 算法导论：第2版[M]. 机械工业出版社， 2007. [通联编辑：王力]