利用函数的性质求解数列问题
邵超群
(江苏省南京师范大学 210024)
一、利用函数的单调性求解数列问题
例1 (2013.上海)在数列{an}中,an=2n-1,若一个7行12列的矩阵的第i行第j列的元素cij=aiaj+ai+aj,(i=1,2,…,7;j=1,2,…,12),则该矩阵元素能取到的不同元素的个数为( ).
A.18 B.28 C.48 D.63
分析解决这道题目首先要理解不同元素的意思,即元素不重复.由于该矩阵的第i行第j列的元素cij=aiaj+ai+aj=(2i-1)(2j-1)+2i-1+2j-1=2i+j-1(i=1,2,…,7;j=1,2,…,12),要使aij=amn(i,m=1,2,…,7;j,n=1,2,…,12)(找出重复元素),则满足2i+j-1=2m+n-1,得到i+j=m+n.由指数函数的单调性可知:当i+j≠m+n时,aij≠amn,因此即可得出该矩阵元素能取到的不同数值是i+j(i=1,2,…,7;j=1,2,…,12)的所有不同和.
解答该矩阵的第i行第j列的元素cij=aiaj+ai+aj=(2i-1)(2j-1)+2i-1+2j-1=2i+j-1(i=1,2,…,7;j=1,2,…,12),当且仅当i+j=m+n时,aij=amn(i,m=1,2,…,7;j,n=1,2,…,12).因此该矩阵元素能取到的不同数值为i+j的所有不同和,其和为2,3,…,19,共18个不同数值.故选A.
反思由题意得出:当且仅当i+j=m+n时,aij=amn(i,m=1,2,…,7;j,n=1,2,…,12)是解题的关键.

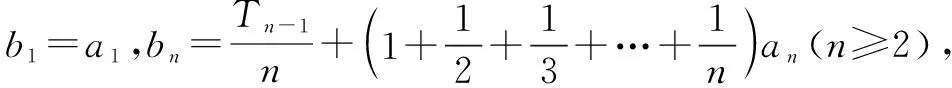
解(1)、(2)略;

反思数列问题中像第三问这种不等式的证明高考题中很常见,常常需要运用分析法,把问题转化为一个个熟悉的问题进行求解.例如本题是转化为一个新的函数,最终利用函数的单调性证明,在这个过程中常常会使用放缩法等有技巧性的手段.教师在实际的解题教学中可以简要地介绍几种常见的放缩结构,注意把重点放在问题的分析上.
二、利用函数的周期性求解数列问题
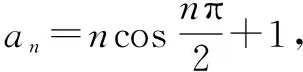
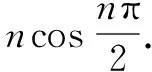
解该数列前2012项和可分为两部分求解:一部分是常数项1求和,其和为2012;
反思由三角函数周期性化简求和是解题的关键,教师在平时教学过程中应多注意引导学生将数学和三角函数的性质多做联系,培养学生的发散性思维,而不是沉浸于“题海战术”.
例4 (2009.北京)已知数列{an}满足:a4n-3=1,a4n-1=0,a2n=an,n∈N*,则a2009=____;a2014=____.
解本题表面上是数列递推,2009=4×503-3,则a2009=a4×503-3=1;同理a2014=a2×1007=a1007=a4×252-1=0.但本质上是体现着数列(函数)的周期性,如果把数列看作是一个抽象函数f(x),我们很快就能得到f(1)=f(5)=…=f(4x-3)=1(x∈N*)、f(3)=f(7)=…=f(4x-1)=0(x∈N*)、f(1)=f(2)=…=f(2x)(x∈N*).根据上述几个关系式,易知当数列取到奇数项时,呈现出1,0周期为2的交替数列;而当为偶数项时,是恒为1的常数列.因此a2009=a1004×2+1=a3=1,a2014=a1=0.显然从函数(周期性)能更清晰地理解本题的数列递推.
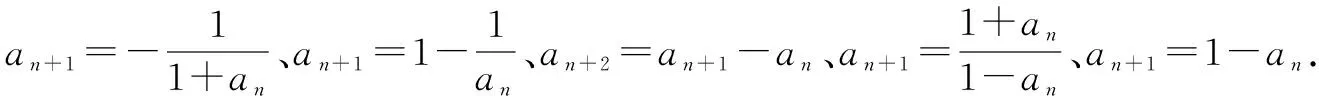
例5 (2012年苏锡常镇一模)设u(n)表示正整数n的个位数,a(n)=u(n2)-u(n),则数列{an}的前2012项和等于____.
分析高中阶段求数列前n项和,要么是通项公式比较特殊(等差、等比等),要么是前后项之间有一部分可以化简(裂项相消这种形式),还有一种就是根据周期来求.本题新定义的这个数列均不属于前两种,那它是否具有周期性呢?这就是我们要考虑的.
解因为u(n)是表示正整数n的个位数,而我们发现a(n)=u(n2)-u(n) 是周期为10的数列,一个周期内各项为:0、2、6、2、0、0、2、-4、-8、0,一个周期内各项之和为0,所以前2012项和实际就是前两项值和为2.
反思这种新定义的数列是近年高考的常考题,实际上只要弄清它的定义法则就很简单了.比如本题u(n)的周期为10这是很容易看出的,那么u(n2)是否也具有周期性呢,结合它的定义法则很容易就可以得到它的周期也为10,只要绕过这道关,问题就解决了.
三、利用函数的对称性求解数列问题
这里的函数并不是指所有函数,而是指在正整数集上的某一区域内对称轴的函数,比如二次函数,三角函数等等,遇到与这些函数有关的数列问题时,我们可以往这方面考虑,常常能起到事半功倍的效果.

例6 已知等差数列{an}的前n项和为Sn,a1=16,S5=S12.当n为何值时,Sn有最大值,并求出其最大值.
分析等差数列的前n项和是关于x的二次函数的离散点,又由于Sn有最大值,说明图象开口朝下d<0,因此它的最大值可能有两项,需要进一步分析.


反思从二次函数图象的对称性角度,可以更加直观便捷地解决此类问题,并且符合学生的认知,从而更加自然地列出关系式,这也更容易帮助学生理解等差数列前n项和的性质.

