运用图像重构误差控制的骨架简化方法
段汕,毛振帼,谢长江
(中南民族大学 数学与统计学学院,武汉 430074)
1 问题的引入
自BLUM提出基于中轴变换[1]的骨架提取方法开始,各种骨架提取算法相继涌现,这些方法所提取的骨架可以用于形状描述,但大多包含大量的冗余骨架成分,且基于中轴变换所提取的骨架对边缘噪声往往较为敏感,使骨架稳定性受到影响. 针对这个问题,研究者们提出了许多改进方法[2-6],其中FELDMAN J和SINGH M对形状骨架的优化提取进行了相关研究[7],提出获取最大后验概率(MAPS)的贝叶斯模型方法,将贝叶斯法则运用于骨架生成,建立了最优骨架提取的算法框架. SHEN W[8]以及秦红星[9]等人则通过对贝叶斯模型方法的改进,提出了基于中轴的骨架修剪方法,这些方法能有效地提取简洁且能较为准确地表示形状的骨架成分.
本文在相关研究成果的基础上,将贝叶斯模型方法运用于基于图像重构误差控制下的骨架简化问题,通过建立平衡算法实现重构精度与骨架简化的平衡统一. 利用重构误差及骨架简洁度作为控制参数,对图像中轴所包含的骨架分支进行优选. 在算法的设计中,通过对骨架分支级别的设置,运用控制参数和平衡算法,在骨架主轴的基础上通过添加相关各级别的骨架分支,实现对骨架分支的优选,最终获得图像的最优近似骨架.
2 骨架相关基本概念
本文主要通过对形状中轴进行简化来获得最优近似骨架,为了更明确地说明骨架结构,首先给出一些相关概念.
目标对象X的外形轮廓称为形状. 按照BLUM关于中轴的定义,嵌入形状X内部且与X至少在两点相切的最大圆盘圆心的全体称为形状X的中轴,记为M. 形状X的骨架是与中轴M具有相同拓扑结构的M的任一子集,记为S.
若骨架点s(s∈S)的八邻域内有n个骨架点,则称其度为n(0≤n≤8),见图1.骨架上半径最大的圆盘的圆心称为骨架中心点(如图2中的点o). 由骨架点到其八邻域中邻接骨架点的方向称为正方向.
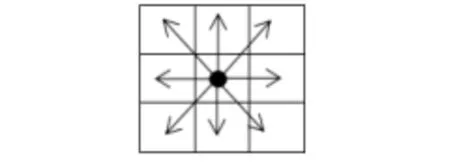
图1 骨架点八邻域示意图Fig.1 Schematic diagram of the eight domain of skeleton point
设H为骨架上所有分支点(度大于2)的集合,将中心点与H中所有点之间的最长路径称为骨架主轴.若该路径方向的反方向上存在H中的点,则该点与中心点间的路径与原骨架轴合并成新的骨架轴. 如图2所示,路径L(o,p1)最长,但在其反方向上存在H中的点p2,则将路径L(o,p1)与L(o,p2)合并成骨架主轴L(p1,p2).
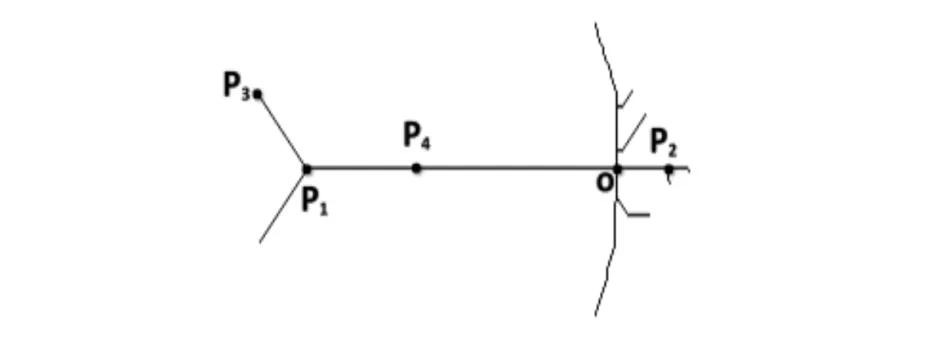
图2 骨架结构示意图Fig.2 Schematic diagram of skeleton structure
根据文献[10],若将骨架视为几何图,则骨架由有限个连接弧组成,这些连接弧称为骨架分支.由骨架主轴(亦称为零级骨架分支)沿着近似垂直于其外法线方向的最长骨架分支称为一级骨架分支,由一级骨架分支沿着近似垂直于其外法线方向的最长骨架分支称为二级骨架分支,以此类推,n级骨架是由n-1级骨架分支沿着近似垂直于其外法线方向的最长骨架分支.
图2中路径L(p1,p3)为一级骨架分支.
基于骨架S的形状X的重建R(S)可以表示为:
(1)
其中B(s,ρ(s))是以s为圆心,ρ(s)为半径的圆盘,ρ(s)表示骨架点s∈S所对应的最大圆盘半径,θρ(s)=ρ(s)Bo=B(s,ρ(s)),Bo为单位圆盘,δθρ是以θρ(s)为结构元的形态膨胀变换.
若S=M,则R(S)=M,即由中轴M可以完全重构形状X. 受边界噪声和扰动的影响,中轴M往往包含着一些伪骨架分支,且其构成较为复杂,在(1)式的重构成分中存在大量的冗余.针对中轴的这一特点,许多学者对中轴进行了修剪,以达到对中轴的简化,所获得的骨架仅保留中轴的主体骨架成分,且含有足够多的信息,可使重构图像达到某一个精度范围.本文以此为研究目标,将贝叶斯模型方法运用于基于图像重构误差控制下的骨架简化问题,通过建立平衡算法实现重构误差与骨架简化的平衡统一.利用重构误差及骨架简洁度作为控制参数,对图像中轴所包含的骨架分支进行优选.在算法的设计中,通过对骨架分支级别的设置,运用控制参数和平衡算法,在骨架主轴的基础上通过添加相关各级别的骨架分支,实现对骨架分支的优选,最终获得图像的最优近似骨架.
3 平衡算法
费尔德曼等学者[7]所提出的基于贝叶斯估计的最大后验骨架MAPS(the maximum a posteriori skeleton)生长算法是实现重构精度与骨架简化平衡统一的一种策略,它通过引入基于骨架的重构误差及描述骨架简洁性的简洁度两个量化指标,以同时达到低误差和高简洁度的平衡为目标,提出了形状骨架的优化算法.
3.1 贝叶斯平衡策略
贝叶斯模型方法[7]的基本思想是将骨架的形成视为一随机生长过程,运用贝叶斯法则:
(2)
提供平衡策略,这里Sj是构成骨架S的有限个连接弧. 似然函数P(X|S)可视作骨架生长模型,用于刻画骨架生长的准确度. 骨架的简洁度定量描述为骨架分支少且分支曲率小,采用先验概率P(S)加以刻画,所涉及的概率分布均采用指数分布作为近似.
对于(2)式中的分母,由全概率公式有:
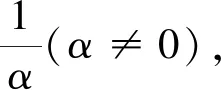
P(S|X)=αP(X|S)P(S),
(3)
最终的近似骨架由
S*=argmin(-logP(S|X))
(4)
产生.
3.2 重构误差与骨架简洁度
本文将贝叶斯骨架生长模型方法[7]的基本思想运用于对中轴的修剪上,以获取最优近似骨架.首先要解决的问题是,如何基于中轴对重构误差和骨架简洁度进行具体量化.通过文献[8]可知,重构误差的一个常用的估计方法是通过设置:
(5)
对误差进行测量,这里Λ(·)是基于像素或区域的面积测量运算. 骨架的生长模型P(X|S)所描述的是基于骨架的重构图像与原始图像的相似程度,相似程度越高即重构误差越小.由文献[8]可知,重构误差近似服从指数分布,故取:
P(X|S)∝exp(-λσ),
(6)
其中λ为分布参数.
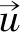
(7)
(8)
利用Von. Mises分布[7]特点,所有n级骨架分支关于n-1级骨架分支转角误差之和θ服从Mises分布. 若将Z=eiθ作为随机变量,则θ~V(0,b),即:
P(θ)∝exp(cosbθ).
(9)
骨架分支数量是对骨架简洁度的另一衡量标准,骨架越简洁,其包含的分支越少,分支的总长度μ(S)就越小,优选骨架点落在最优近似骨架上的可能性就越大,这意味着骨架简洁度P(S)与μ(S)成反比:
(10)
其中分母的设计使得P(S)∈[0,1].
3.3 平衡公式
利用贝叶斯平衡策略的基本思想,在以上关于骨架重构误差和骨架简洁度量化表示的基础上,利用(5)~(10)式及相关变量所服从的分布特点,引入平衡公式:
(11)
这里a,b为控制参数,β为比例系数,参数及系数都将通过对图像进行大量算法实验,对实验结果作对比调整而得. (11)式表明:骨架各级分支转角误差越小,所对应的分支对重构图像贡献越大;重构误差越小,基于骨架的重构图像与原始图像的匹配度越高,当两者同时达到最小时,平衡公式(11)将输出最大值,此时骨架S对图像X描述的准确度最高. 因此,最优近似骨架应满足f(θ,σ|S)取得最大值,即
maxf(θ,σ|S)⟺min(-logf(θ,σ|S)),
因此,最优近似骨架产生于:
S*=argmin(-logf(θ,σ|S)).
4 修剪算法
本节将在以上所研究的骨架提取平衡算法的基础上,给出获取最优近似骨架的具体实现方法. 本文提出的简化方法相对于常规方法是一个逆向的过程,采用以由中轴所确定的骨架主轴,即零级骨架为基础的、平衡公式控制下的各级骨架分支逐级迭代添加的方法,最终获取最优近似骨架. 优化算法具体实现过程包含以下几个步骤:
1)确定骨架主轴S(0):以中轴作为初始骨架,根据第二小节的定义,确定中心点,运用八邻域法搜索计算得到主轴,称为零级近似骨架成分;
2)向骨架主轴从低到高逐级添加各级骨架分支:当近似骨架达到所设定的重构精度时,停止迭代添加;
3)各级近似骨架成分迭代生成方法:令Ei(i=1,2,…,n)为添加入第i-1级近似骨架成分的i级骨架分支,则有以下递推关系式:
S(0)=S,S(i)=S(i-1)+Ei.
(12)
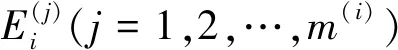
(13)
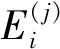
(14)
其中η为一个不大的正数,运用max函数可以提取出简洁度与重构误差度比重最大的骨架分支,即又短又直且包含形状拓扑信息多的骨架分支.用arg函数求出大权重值对应的那些分支,即构成所添加的第j个i级骨架分支:
(15)
5)最优近似骨架:利用迭代公式S(i)=S(i-1)+Ei,重复上述过程,直到最新获得的近似骨架成分S(i)满足Λ(X-R(S(i)))≤ε,则终止执行,此时的S(i)即为所求最优近似骨架.
5 实验检测
算法测试利用MATLAB编程实现,中轴是由MATLAB自带的骨架提取函数产生的. 取β=1,b=10,a=1/π来进行如下所有实验.
本节将从算法有效性、骨架重构质量、骨架稳定性、算法优越性等几个方面来进行实验.为了说明本文算法的有效性,选取以下几幅图形进行实验.
图3(a)为输入图形及中轴,图3(b)为本文算法获得的骨架以及重构形状,图3(c)为重构误差图. 实验结果显示图3(b)中各骨架分支能较好地对应到形状的各个部分,跟图3(a)相比,本文算法所得骨架不仅保留了形状的拓扑信息且结构更加简洁,误差也仅仅表现在图像极少部分边界上.
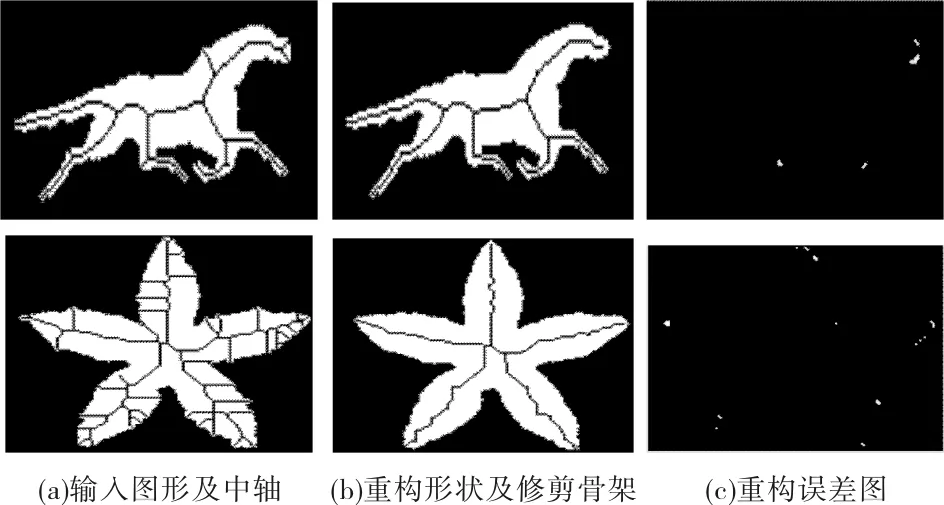
图3 几组图形的骨架修剪结果及重构对比实验Fig.3 Results of skeleton pruning and reconstruction contrastive experiment of several groups of graphics
表1给出了图3中相关重构误差率及骨架长度对比差值. 表1的数据和图3的视觉效果显示:在对图像的描述上,本文算法得到的骨架不仅具有良好的准确性,同时所占用的储存空间相对较少.

表1 图3中各个形状的骨架重构误差率及骨架长度差Tab.1 The error rate of skeleton reconstruction and the difference of skeleton length in each shape inFig.3
为了说明本文算法的稳定性,选取两组形状来进行测试,通过对形状边界进行一定程度的干扰来检测骨架的变化情况.
图4(a)为无噪声情况下提取的中轴,图4(b)为无噪声情况下本文算法所提取的骨架;图4(c)为加噪声情况下提取的中轴,图4(d)为加噪声情况下本文算法所提取的骨架. 通过对比可以看出,边缘噪声干扰对中轴的影响较大,但本文方法获得的骨架则表现出较好的稳定性.

图4 骨架的稳定性对比实验Fig.4 Comparison experiment on the stability of skeleton
为了表明本文算法在骨架简洁效果上的改进,本文选取了一个规则形状的大写字母E、不规则形状乌龟和树与文献[8]中的方法进行对比测试.
图5(a)为中轴,图5(b)为用文献[8]提出的方法简化得到的骨架,图5(c)为本文算法简化得到的骨架. 由实验结果可以看出,与文献[8]方法提取的骨架相比,本文的方法在处理规则形状以及一些小分支上效果更好.
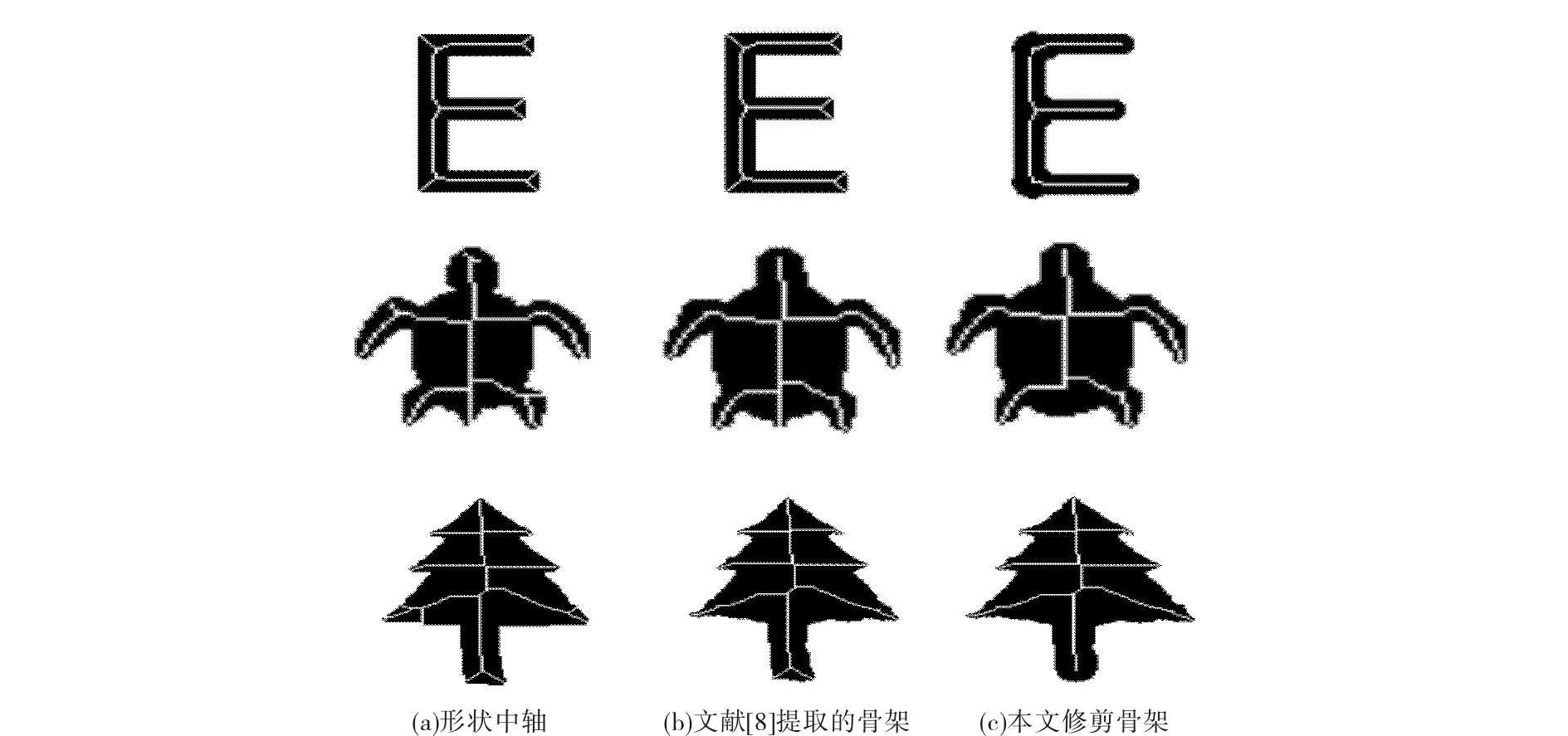
图5 本文方法与文献[8]方法间的骨架修剪对比实验Fig.5 Comparison of skeleton pruning experiments between the method of this paper and the method of reference[8]
为了便于对两种方法进行对比,引入有效率指标:
(16)
该公式表明,重构误差率越小、骨架简洁度越高时,有效率越大,骨架整体效果也会越好. 针对两个不规则形状,表2给出了与文献[8]方法进行对比的结果(E属于规则图形,故未纳入表2).

表2 图5中不规则形状的数据对比Tab.2 Comparison of data of irregular shapes inFig.5
除此之外,本文还做了一组与文献[9]方法的对比测试实验.
图6(a)为形状中轴,图6(b)为文献[9]方法修剪得到的骨架,图6(c)为本文算法修剪得到的骨架,其重构数据对比见表3.

图6 本文方法与文献[9]方法间的骨架修剪对比实验Fig.6 Comparison of skeleton pruning experiments between the method of this paper and the method of reference[9]

形状重构误差率σ本文方法文献[9]骨架简洁度P(S)本文方法文献[9]有效率ω本文方法文献[9]骆驼0.06000.0445O.00310.00343.23.0
表2和表3中有效率一栏是(16)式计算结果扩大1000倍得到的数据. 将文献[8]、文献[9]与本文相关数据进行对比,尽管本文的重构误差率高于其他两种方法,但本文算法的重构误差是可以控制的,并且获得的重构图像在形状上仍然保留着原图像大部分的形状和拓扑特征. 通过控制重构误差,本文的骨架简洁率优于文献[8]和文献[9],并且有效率也优于这两种方法,这表明本文方法在骨架简洁度以及整体效果上更好.
除此之外,本文的方法在运算速度上也快于文献[8]和文献[9]的方法. 文献[8]与文献[9] 给出的算法每次迭代只能优选出一条骨架分支,而本文可以一次性选取多条符合条件的骨架分支,从而减少了迭代次数. 另外,文献[8]和文献[9]每次迭代修剪时都会保存当前骨架,在完成所有分支删减后,还要将所有迭代产生的一系列不同的骨架再进行一次对比运算,才能最终产生出优选骨架,而本文则直接在骨架主轴上添加各级分支,以更新骨架直到骨架到达指定重构误差才停止运算. 从这个方面来说,本文的算法复杂度较低,运算速度也优于文献[8]和文献[9],且这种优势在越复杂的形状处理上体现得越充分.
6 结语
本文通过改进费尔德曼和辛格提出的贝叶斯模型,建立了一个用于骨架简化的平衡公式,利用平衡公式将满足条件的骨架分支迭代添加入骨架主轴中,以获得最优近似骨架. 同时本文还从算法有效性、骨架重构质量、骨架稳定性、算法优越性等几个方面进行了实验测试,实验结果表明本文的算法是有效的,本文方法所获得的近似骨架不仅简洁且能保证良好的形状视觉呈现. 相比其他同类方法,本文方法在骨架简洁性、整体效果以及运算速度等方面都有所改进.

