基于二参数寻优设计点的混合结构可靠性分析算法
邱涛, 张建国, 邱继伟, 魏娟, 游令非
(1.北京航空航天大学 可靠性与系统工程学院, 北京 100191;2.北京航空航天大学 可靠性与环境工程技术国防科技重点实验室, 北京 100191;3.中国兵器工业标准化研究所, 北京 100089)
0 引言
在机械产品可靠性分析过程中,受加工尺寸、材料性能等条件的限制,往往需要考虑大量的不确定性。对于部分统计信息不足的不确定变量,难以得到对应的精确分布,可以采用区间变量对其进行表述。因此,研究概率-区间共存的可靠性问题具有一定的工程价值[1]。
针对概率-区间混合的可靠性问题,Kang等[2]采用单层优化模型将区间变量嵌入寻优设计点(简称MPP)的优化问题中。王骞等[3]通过构建响应面的方法求解最大失效概率。Xie等[4]提出一种单循环算法,将区间优化的Karush-Kuhn-Tucker(KKT)最优条件作为MPP搜索的约束条件。Du[5]提出了基于一次二阶矩的统一不确定分析算法。姜潮等[6]考虑极限状态带的两种不同构形,采用了基于响应面的混合可靠性算法。Elishakoff等[7]研究了不确定性的概率模型和凸模型混合问题。Xie等[8]用高维模型表示功能函数,将混合可靠性问题转化为单步可靠性计算模型。宋向华等[9]利用非概率理论解决了混合可靠性问题。刘瞻等[10]基于Kriging模型和重要抽样法进行了混合模型的可靠性分析。Du[11]提出了一种序列迭代算法,通过区间分析和概率分析的反复迭代求解,使随机变量和区间变量同时收敛至最优解。Zhang等[12]利用积分方法求解了概率-区间混合的失效概率。
目前,针对极限状态函数非线性程度较高的可靠性问题,计算结果的收敛稳定性与效率是该问题的关键。通过解耦双层优化模型,对外层进行概率分析,对内层进行区间分析实现高效序列迭代。虽然一些概率分析算法(如Hasofer-Lind和Rackwitz-Fiessler(HLRF)算法等[13-16])能够直接进行可靠度计算,但存在结果不收敛的问题。在概率分析时,通过引入两个调整参数η和λ,分别调整搜索步长和搜寻方向,改进了传统的寻优MPP算法;在区间分析时,将功能函数进行2次泰勒近似,并转化为易于求解的2次规划问题,为解决概率-区间混合的可靠性问题提供了一种新的算法。最后,通过两个案例验证了该算法的精度、效率及稳定性。
1 概率- 区间混合可靠性双层优化模型
机械结构中既存在随机变量又存在区间变量,则功能函数可以表示为
Z=g(X,Y),
(1)
式中:X=[X1,X2,…,Xn]T为n维随机向量;Y=[Y1,Y2,…,Ym]T为m维区间向量。当构件发生故障,即g(X,Y)≤0时,失效概率Pf定义为
Pf=Pr{g(X,Y)≤0}.
(2)
如图1所示,X1、X2为随机变量,功能函数因含区间变量Y,g(X,Y)=0在随机空间中不再是一个曲面,而是由两个边界面构成的极限状态带。可以通过(3)式和(4)式来定义失效概率的范围:
(3)
(4)
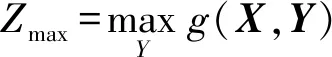
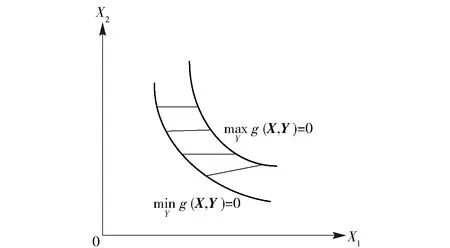
图1 极限状态区域Fig.1 Limit state area
通过将随机变量转换为独立的标准正态随机变量,上述问题可以转换为求解如下两个优化问题,最大和最小可靠度指标分别为
(5)
(6)
式中:U为随机变量转换到标准正态空间内的值;G(U,Y)为随机变量转换到标准正态空间下功能函数的值;βU为可靠度指标最大值,βL为可靠度指标最小值,对应的最大和最小失效概率分别为
Pfmax=Φ(-βL),
(7)
Pfmin=Φ(-βU).
(8)
失效概率的范围为Pfmin≤Pf≤Pfmax,但在实际工程问题中,人们通常关心最大失效概率。因此本文所提算法将以求解最大失效概率Pfmax为例进行混合可靠性分析。
2 混合可靠性分析
针对第1节(6)式中的概率-区间混合可靠性模型,提出一种基于二参数寻优MPP的概率-区间混合可靠性分析算法。如图2所示,该算法分为概率分析和区间优化两部分,二者的计算效率共同决定着混合可靠性的计算成本。在随机变量迭代中,采用基于二参数寻优MPP的概率分析迭代算法;在区间变量迭代中,首先将区间优化问题转换为2次规划问题,再结合梯度投影法进行区间优化分析,求解区间最优点。

图2 序列迭代计算流程Fig.2 Calculation process of sequence iteration
为提高双层优化模型的计算效率,将双层优化模型解耦为概率分析和区间分析的序列迭代可靠性模型。一旦满足收敛条件,则得到最大失效概率点U*,最大失效概率为

(9)
2.1 概率分析
2.1.1 一次二阶矩算法和改进的一次二阶矩算法
Hasofer等[13]和Rackwitz等[14]提出了HLRF一次二阶矩算法,其寻优设计点为
Uk+1=Uk+dk,
(10)
式中:Uk为第k次迭代的MPP;Uk+1为第k+1次迭代的MPP;dk为搜索方向,
(11)

当经过有限次迭代结果收敛后,则收敛点即为MPP. 虽然上述HLRF算法迭代效率较高,但当功能函数非线性程度较高时,此算法不能保证收敛。因此,基于不确定一维搜索准则的改进的一次二阶矩(iHLRF)算法[17]被提出来,其迭代搜索设计点为
Uk+1=Uk+λkdk.
(12)
根据Armijo准则:
(13)
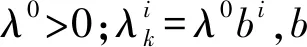
(14)
ck为惩罚参数,且ck>0,mk(U)梯度可表示为
(15)
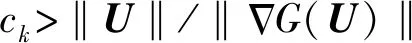
2.1.2 基于二参数寻优MPP的概率分析
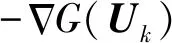
设当前迭代步骤为第k+1次,在随机变量迭代过程中,区间变量保持不变,故在以下寻优MPP算法中省略区间变量。
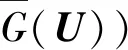
(16)
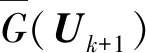

图3 功能函数及其在Uk点处的切平面Fig.3 Performance function and its tangent plane at point Uk

(17)
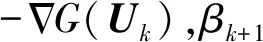
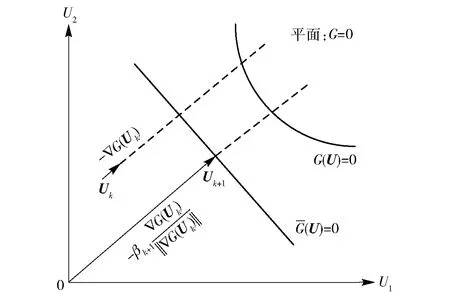
图4 在平面G=0上寻优MPPFig.4 Optimizing MPP on plane G=0
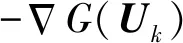
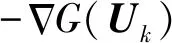
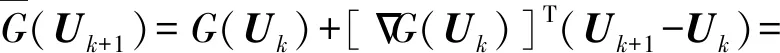
(18)
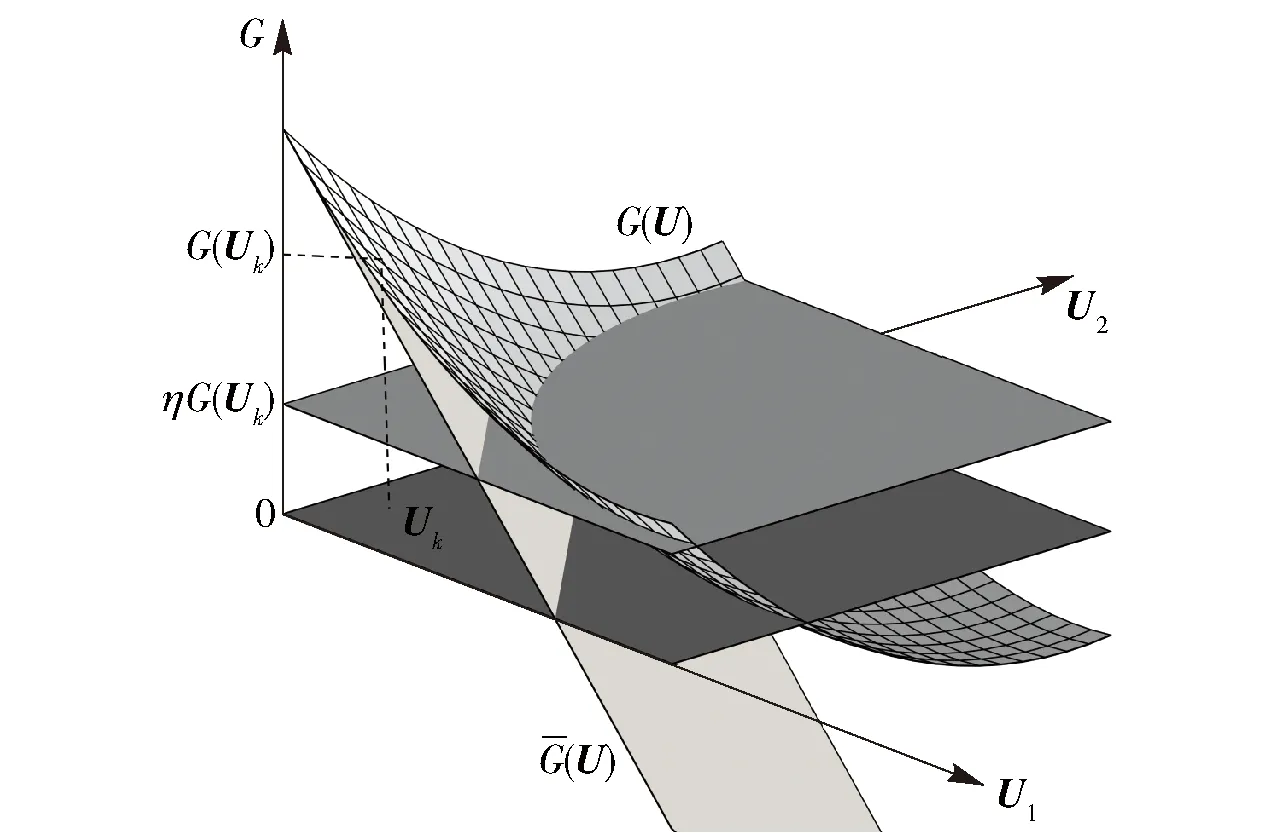
图5 选定η确定平面G=ηG(Uk)Fig.5 Selecting η to determine the plane G=ηG(Uk)

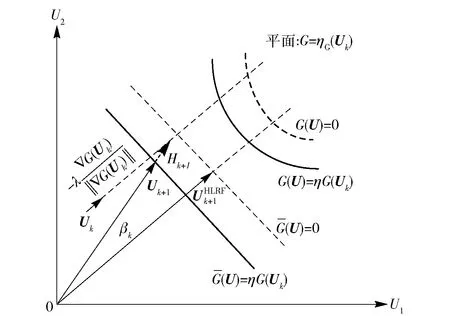
图6 在G=ηG(Uk)平面上寻优MPPFig.6 Optimizing MPP on the plane G=ηG(Uk)

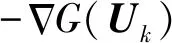
(19)
在平面G=ηG(Uk)上,原点连接到辅助点Hk+1的方向即为Uk+1的搜索方向,Uk+1的方向余弦矢量αk+1为
(20)

Uk+1=βk+1αk+1,
(21)
式中:βk+1为第k+1次迭代的可靠度指标。
将(21)式代入(18)式,得

(22)
求解(22)式,得可靠度系数βk+1为
(23)
根据得到的可靠度系数βk+1,可由(21)式得第k+1次迭代的MPPUk+1.
通过引入两个调整参数分别控制搜索步长和搜索方向,通过参数η调整搜索步长,使功能函数为高度非线性时,寻优MPP收敛成为可能;通过参数λ调整搜索方向,来提高寻优MPP的效率。在选择λ时,可以将其设定为较大的值,一般取λ最大值为50,在具体的迭代中,可以设定λ=λ/c以自适应更新迭代步长,c为步长的调整系数,是一个大于1的常数,根据数值分析,c最好取在1.1~1.3之间。如果λ的初始值较小,则不需要在整个迭代过程中改变λ.
2.2 区间分析
在第k+1次迭代中,利用概率分析求得Uk+1. 根据(6)式表示的双层优化模型,固定随机变量Uk+1,区间分析可表示为(24)式的优化问题:
(24)
式中:Yk+1为第k+1次混合迭代的区间最优点;Yk为第k次混合迭代的区间最优点;YU和YL分别代表区间的上、下界矢量。
为提高计算效率,在进行区间优化之前,首先检查优化问题的KKT条件,KKT优化条件见(25)式和(26)式。若满足KKT条件,则Yk+1=Yk;否则进行区间优化分析[18]。
对于(24)式中的优化问题,KKT条件为
(25)

(26)
式中:j=1,2,…,m表示m维区间变量的第j维。
在区间变量循环迭代中,固定随机变量Uk+1,故在以下区间分析中省略随机变量。设当前迭代循环次数为s,当前迭代点为Ys,功能函数进行2次泰勒展开,(24)式转化为二次规划问题:
(27)
式中:Hs为海森矩阵。
由于(27)式为区间约束的二次规划问题,当约束条件为区间约束时,将迭代方向投影到可行域上进行计算就相当方便,因此可以采用梯度投影法[19]高效地求得功能函数的极限值。首先将迭代方向投影于可行域,再在投影后的最速下降方向上搜索功能函数的第1个局部最优点,最后利用Schur直接法求解最优点。设最优点为Ys(*),则区间变量的迭代过程可表示为
Ys+1=Ys+γsYs(*),
(28)
式中:γs为迭代步长,为保证全局收敛,重复γs←γsρ,直至新迭代点Ys+1满足Arimijo条件,即
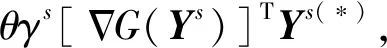
(29)
θ=1×10-4,ρ=0.8.
若新迭代点Ys+1满足KKT条件,则区间迭代停止,Yk+1=Ys+1;否则继续区间迭代。
按照以上算法进行迭代,如果满足‖Uk+1-Uk‖≤ε1且|G(Uk+1,Yk+1)|≤ε2(ε1和ε2是足够小的非负实数),则βL=βk+1,计算最坏情况下的失效概率Pfmax:
Pfmax=Φ(-βL).
(30)
综上所述,本文提出的基于二参数寻优MPP的混合可靠性分析算法流程如下:
1)将随机变量X转化为标准正态随机变量U,得G(U,Y)=0;
2)初始迭代k=0,输入初始值U0和Y0;
3)固定Yk,选择η和λ的值(0≤η<1,λ>0),在G=ηG(Uk)平面上确定Uk+1的搜索方向αk+1,并计算βk+1和Uk+1;
4)检查KKT条件,如果满足则Yk+1=Yk,转步骤6,否则转步骤5;
5)利用梯度投影法与Arimijo条件,计算Yk+1=Ys+1;
6)检查收敛,如果满足‖Uk+1-Uk‖≤ε1且|G(Uk+1,Yk+1)|≤ε2(ε1和ε2是足够小的非负实数),则βL=βk+1,转步骤7,否则k=k+1并转步骤3;
7)计算最坏情况下的失效概率Pfmax=Φ(-βL)。
3 案例分析
为验证所提算法的精度、效率及稳定性,本节通过两个案例进行分析。其中,收敛精度均取ε1=ε2=1×10-6,取λ>2,设定λ=λ/c,c=1.2以自适应更新迭代步长;N1和N2分别为混合可靠性分析循环序列迭代的迭代次数和函数调用次数。
3.1 悬臂梁失效概率计算
如图7和图8所示,在悬臂梁末端施加水平力Fx和垂直力Fy,悬臂梁长度为l、横截面宽度为w、高度为h,l(mm)、w(mm)和h(mm)服从正态分布。悬臂梁的最大应力不超过屈服强度极限值S=380 MPa,Fx和Fy为区间变量,其分布参数如表1所示。
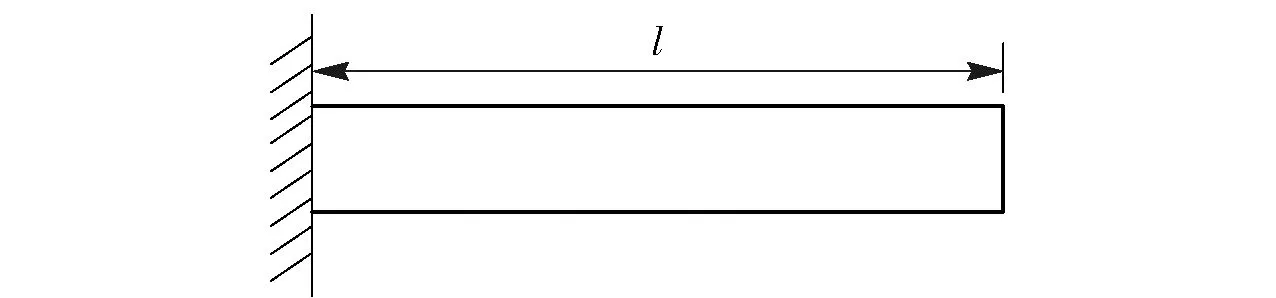
图7 悬臂梁Fig.7 Cantilever beam

图8 悬臂梁横截面Fig.8 Cross section of cantilever beam
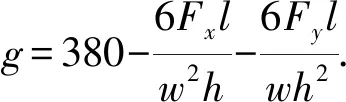
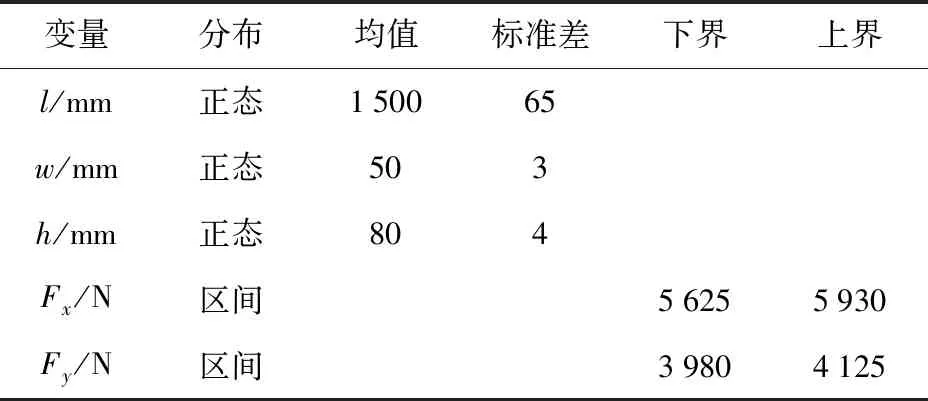
表1 悬臂梁的不确定性特征Tab.1 Uncertainty characteristics of cantilever beam
图9为本文算法与不同混合可靠性分析算法的收敛结果对比。由图9可知,当功能函数非线性程度较低时,相比于基于HLRF/iHLRF混合可靠性分析算法,本文所提算法同样具有较高的收敛效率。表2为η、λ取不同值时的分析结果。由表2可知,随着η的减小、λ的增大,本文所提算法精度基本不变,但收敛效率会逐渐提高。当η在0~1之间取任意值时,λ可取大于0的任意值,且随着λ的增大,收敛效率会提高;当λ取大于0任意值并固定时,η可取0~1之间的任意值,且随着η的减小,收敛效率会提高;当η=0、λ→∞时,本文算法与基于HLRF的混合可靠性分析算法具有相同的计算效率,迭代次数均为4,函数调用次数为53.

图9 本文算法与基于HLRF/iHLRF混合可靠性分析算法的收敛过程对比(η=0.1,λ=0.9)Fig.9 Comparison of the convergence process of the algorithm proposed in this paper and the mixed reliability analysis based on HLRF/iHLRF(η=0.1,λ=0.9)
为验证本文算法的精度,采取蒙特卡洛法(MCS)计算失效概率。首先将每个区间等分为10份,在区间变量的组合值下对随机变量抽取1×108次,则功能函数调用1×1010次。表3为悬臂梁最坏情况下的失效概率。由表3可知,本文算法相对误差为3.9%,与基于HLRF/iHLRF[19]混合可靠性分析算法的函数调用次数为同一数量级,收敛效率基本一致。综上所述,本文算法通过对两个参数的调整,既具有较高的计算精度,又具有较高的收敛效率。
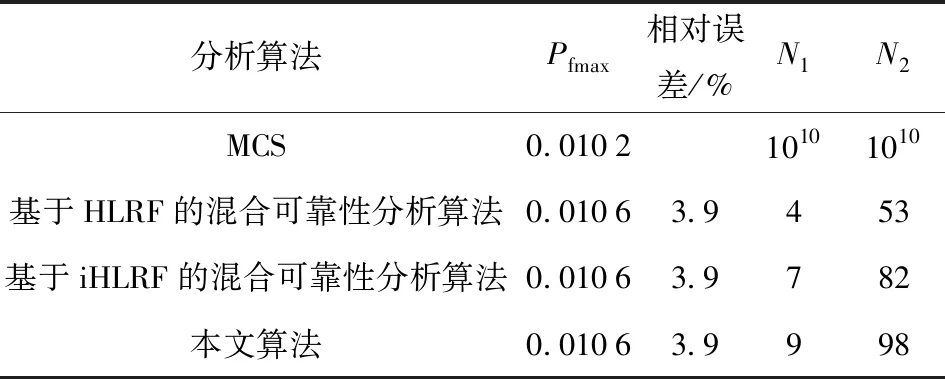
表3 悬臂梁最坏情况下的失效概率Tab.3 Failure probabilities cantilever beam in the worst case
3.2 简支梁失效概率计算
如图10所示,对简支梁施加均布载荷q和集中载荷F,梁的长度为l,杨氏模量为E. 简支梁在C点的挠度不超过极限值δ=6 mm,q和F为区间变量,E、l、w和h服从正态分布,其分布参数特征如表4所示。本例为概率-区间混合的结构可靠性问题,求解简支梁在C点的挠度不超过极限值的最大可能失效概率。
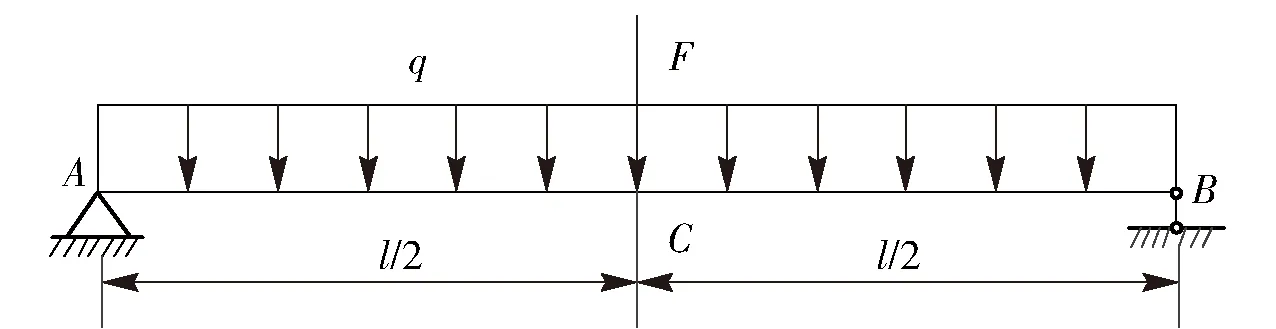
图10 简支梁Fig.10 Simple beam表4 简支梁的不确定性特征Tab.4 Uncertainty characteristics of simple beam
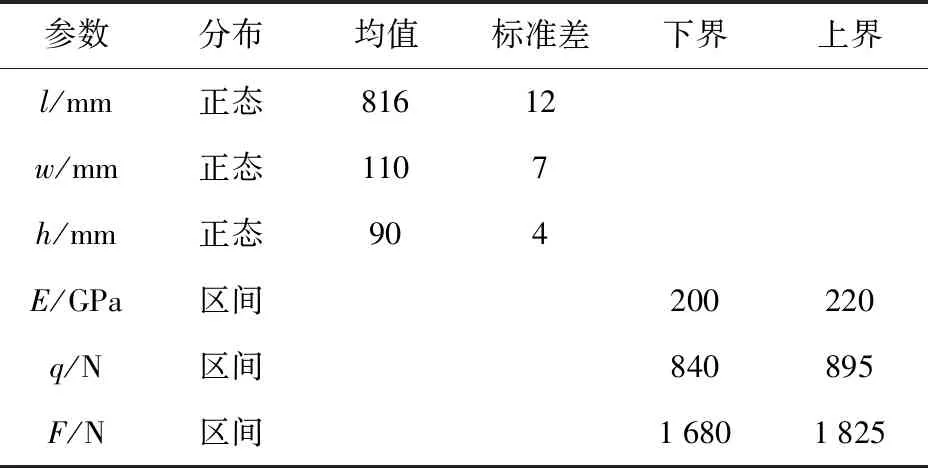
参数分布均值标准差下界上界l/mm正态81612w/mm正态1107h/mm正态904E/GPa区间200220q/N区间840895F/N区间16801825
表5为不同η、λ值时的失效概率分析结果。由表5可知,当功能函数非线性程度较高时,随着η取值减小,λ取值增大,分析结果存在不收敛的情况;当η取值趋于0时,本文算法和基于HLRF的混合可靠性分析算法类似,会存在计算收敛不稳定的问题;当η取值趋于1时,即收敛迭代步长减小,能解决计算结果收敛不稳定的问题,使计算结果收敛;当λ取值增大时,随着沿梯度方向的步长增加,收敛速度变快,但会引起收敛不稳定的问题,此时可以增加步长调整系数c,以自适应调整迭代步长,解决计算收敛不稳定的问题。
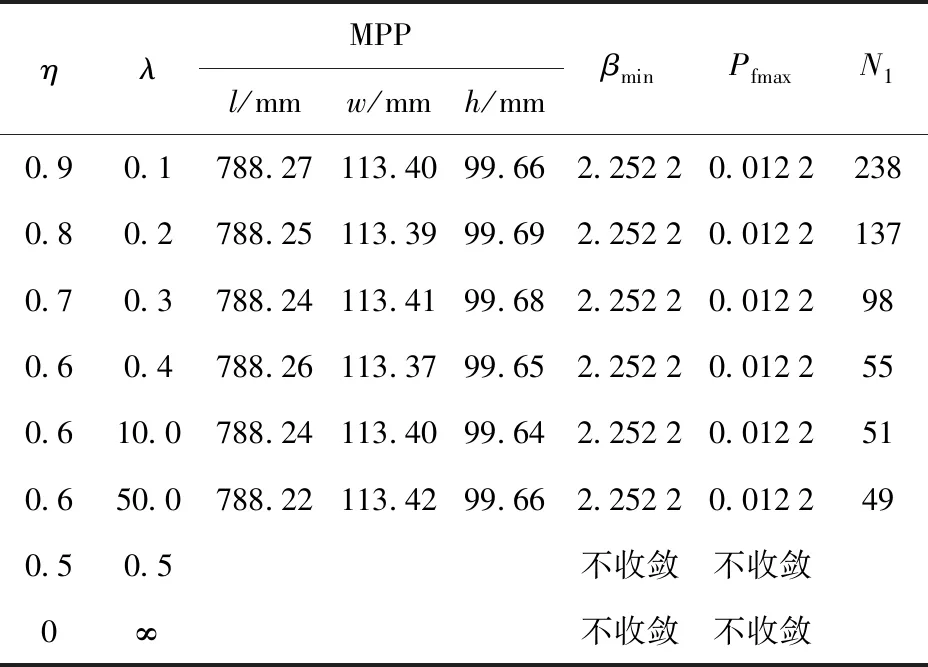
表5 简支梁不同η、λ取值的分析结果Tab.5 Analyzed results of different η and λ values for simple beam
为验证本文算法的精度,将每个区间等分为10份,采用MCS在区间变量的组合值下对随机变量抽取1×108次,则功能函数调用1×1011次。根据图11的不同分析方法收敛结果对比图及表6分析结果误差与效率对比可知,与MCS相比,本文所提算法计算结果相对误差为4.3%. 基于HLRF的混合可靠性分析算法,结果不收敛;基于iHLRF的混合可靠性分析算法,在迭代循环47次、函数调用526次后达到收敛;本文所提算法可在迭代循环50次、函数调用638次后达到收敛。以上对比结果表明,当功能函数非线性程度较高时,通过选定合适的η和λ的值,本文算法能解决收敛不稳定的问题,同时具有较高的计算精度和效率。

图11 非线性程度较高时本文算法(η=0.6,λ=10,c=1.2)与基于HLRF/iHLRF混合可靠性分析的收敛过程对比Fig.11 Comparison of convergence processes of the proposed algorithm (η=0.6,λ=10,c=1.2) and the mixed reliability analysis based on HLRF/iHLRF when the performance function having a high degree of nonlinearity 表6 简支梁最坏情况下的失效概率Tab.6 Failure probabilities of simple beam in the worst case
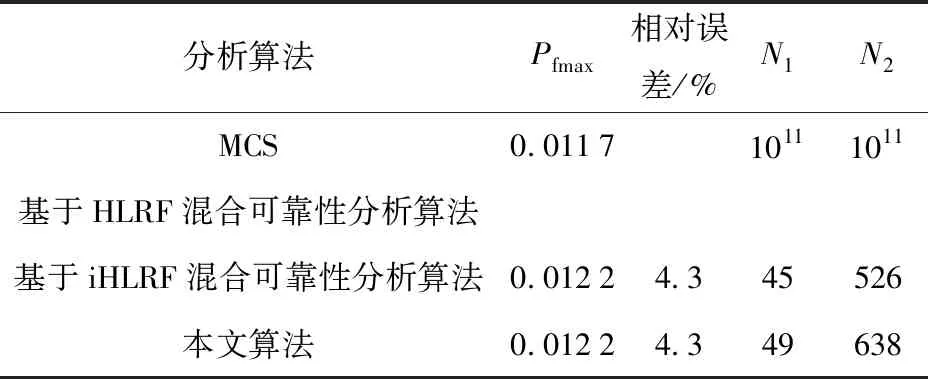
分析算法Pfmax相对误差/%N1N2MCS0.011710111011基于HLRF混合可靠性分析算法基于iHLRF混合可靠性分析算法0.01224.345526本文算法0.01224.349638
4 结论
本文针对机械结构中既有随机变量又含区间变量的混合可靠性问题,提出了基于二参数寻优MPP的混合可靠性分析算法。所得结论如下:
1) 针对概率-区间混合的可靠性问题,可将其转化为双层优化模型,实现概率分析和区间分析共同作用的高效序列迭代算法,使计算结果具有较高的计算精度和效率。
2) 在概率分析时,通过引入两个分别控制搜索方向和搜索步长的调整参数,当功能函数非线性程度较高时,同样能使计算结果收敛,且具有较高的计算效率。

