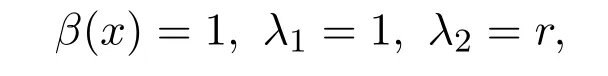关于Tsallis型非对称熵的若干研究

吴贤东,汪加梅,李婉晴

(安徽工业大学数理科学与工程学院,安徽 马鞍山 243032)

1 引言

在统计物理学中,香农熵是最基本的概念,刻画了系统无序性.Tsallis熵是香农熵的一个典型的不可加延伸,在非广延的统计学中扮演了至关重要的角色.

对于随机变量X的概率分布p(x)=p(X=x),Tsallis熵[1]定义为

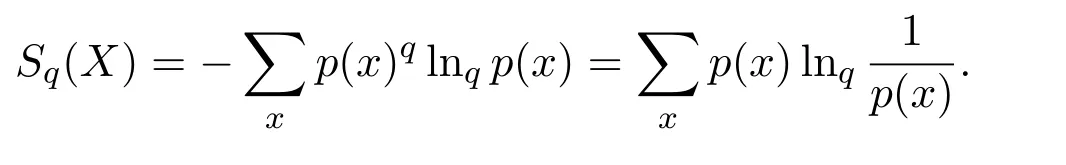
同时,其他的广义熵,如(r,s)-熵、Rényi熵、类型r的熵,统一 (r,s)-熵以及相应的相对熵被引进各种领域,并且对它们的性质进行了深入的研究[2-5].最大熵原理是1957年由文献[6]提出的,它建立了热动力学熵和信息理论熵之间的一个自然对应.由最大熵原理,一些普通的概率分布可以获得,但是一些系统即使是利用一些广义熵的最大熵原理也无法获得.后来,刘成仕通过引进一个辅助参数定义了非对称熵,该熵定义为

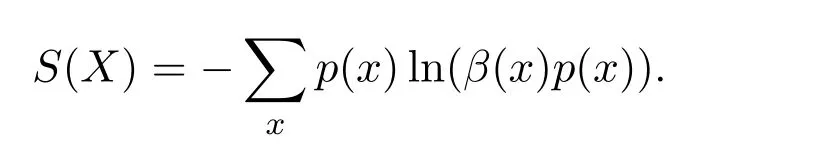
该熵在获得概率分布及幂律方面比起其他的熵更方便[7-8].文献[9-10]研究了最大熵方法的逆问题,就是假设某个概率密度在某种约束下使得熵最大,求这个约束条件.

本文首先定义了Tsallis型非对称熵,该熵包含Tsallis熵Tsallis相对熵,并且非对称熵是该熵的极限情形.因而,非对称熵可以看成是Tsallis型非对称熵的特例.其次讨论了离散情形和连续情形下的Tsallis型非对称熵以及相应的非对称熵原理,并且从这个最大熵原理获得了一些有用的分布.非对称熵可以看成是Tsallis型非对称熵的特例,本文的结果推广了文献[8]的结果.

2 最大的Tsallis型非对称熵原理

令X是一个离散型的随机变量,其取值为{1,2,···,m},且取值为i所对应的概率为

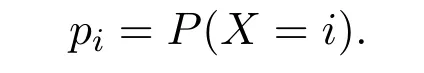
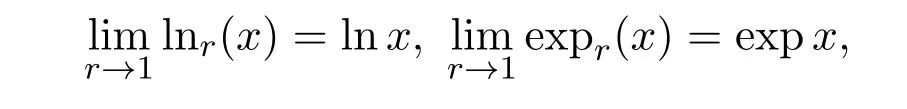
且

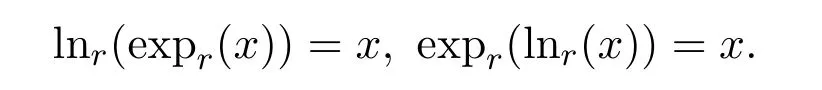
定义2.1 取值为i所对应的Tsallis辅助信息定义为:

其中βj>0是辅助信息参数.相应的,取值为i的Tsallis总信息定义为:

定义2.2 定义离散型随机变量X的Tsallis型非对称熵为如下函数:

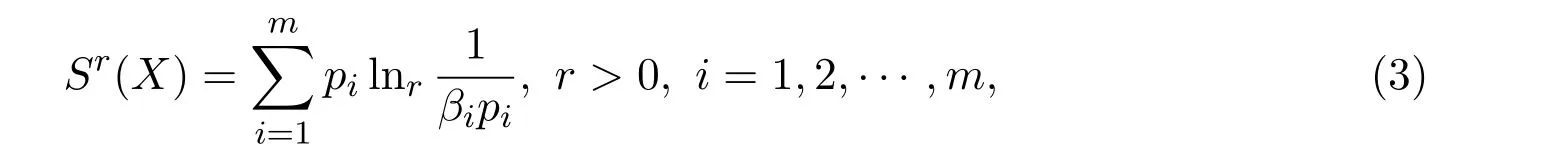
其中βj>0是一个辅助信息参数.

注2.1 由前面的记号,

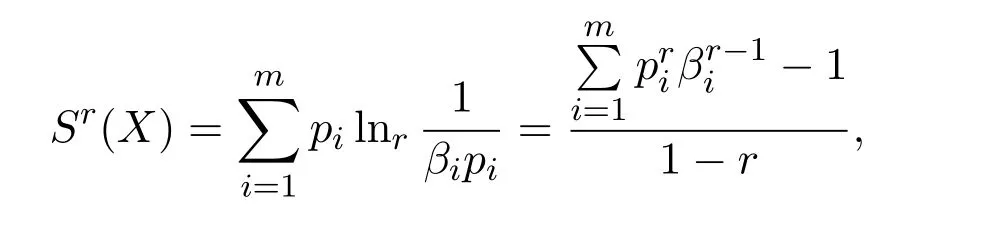
注意到

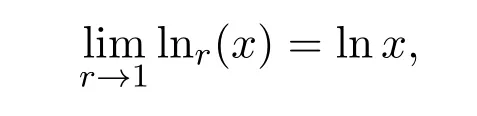
从而

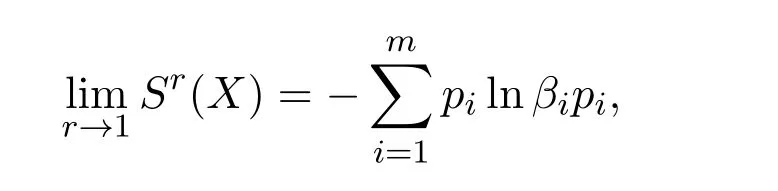
即为非对称熵.

注2.2 在(3)式中,令βi=1,可以得到离散条件下的Tsallis熵:

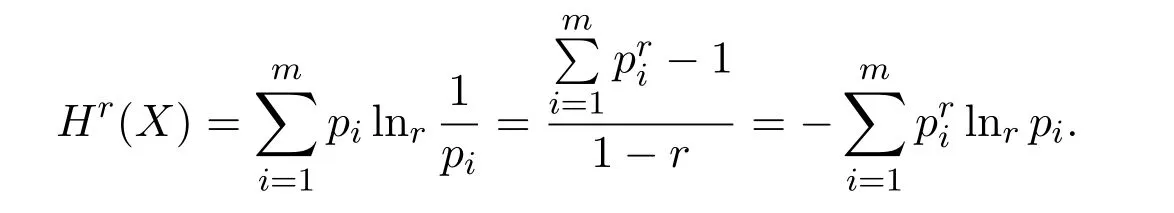
定理2.1(离散情形下的最大的Tsallis型非对称熵原理)如果{p1,p2,···,pm}满足

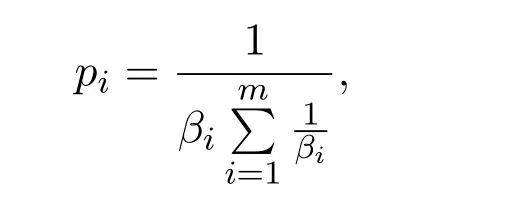
那么Tsallis型非对称熵Sr(X)取得最大值

证明令辅助函数

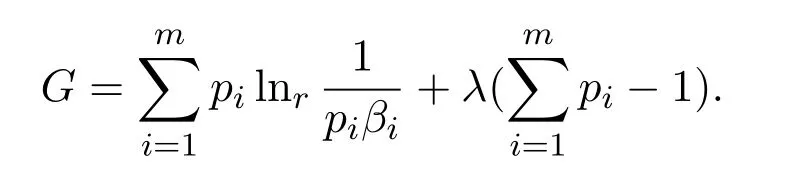
由

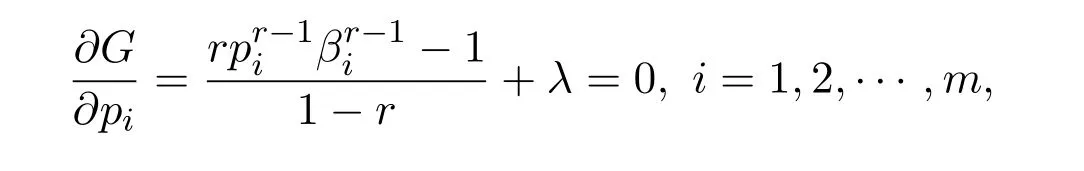
得到

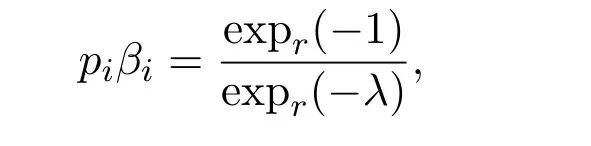
即

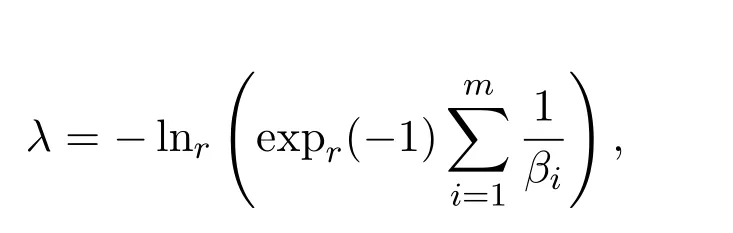
从而

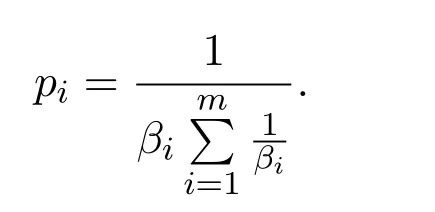
所以,可以得到

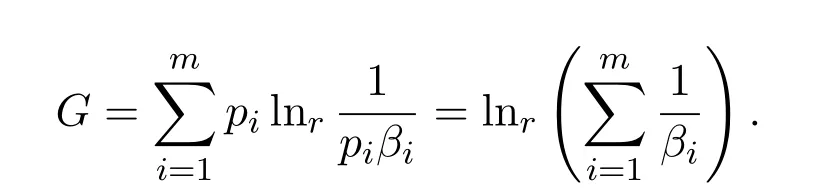
注2.3 取βi=iα,那么由 (5)式知

下面给出定理2.1的等价表述:

定理2.2 若存在一个概率分布P0=(p01,p02,···,p0m),使得

是一个与Pi无关的常数,那么P0是最大的Tsallis型非对称熵的分布,且是最大的Tsallis型非对称熵.

证明对于任意的概率分布P={p1,p2,···,pm},有:

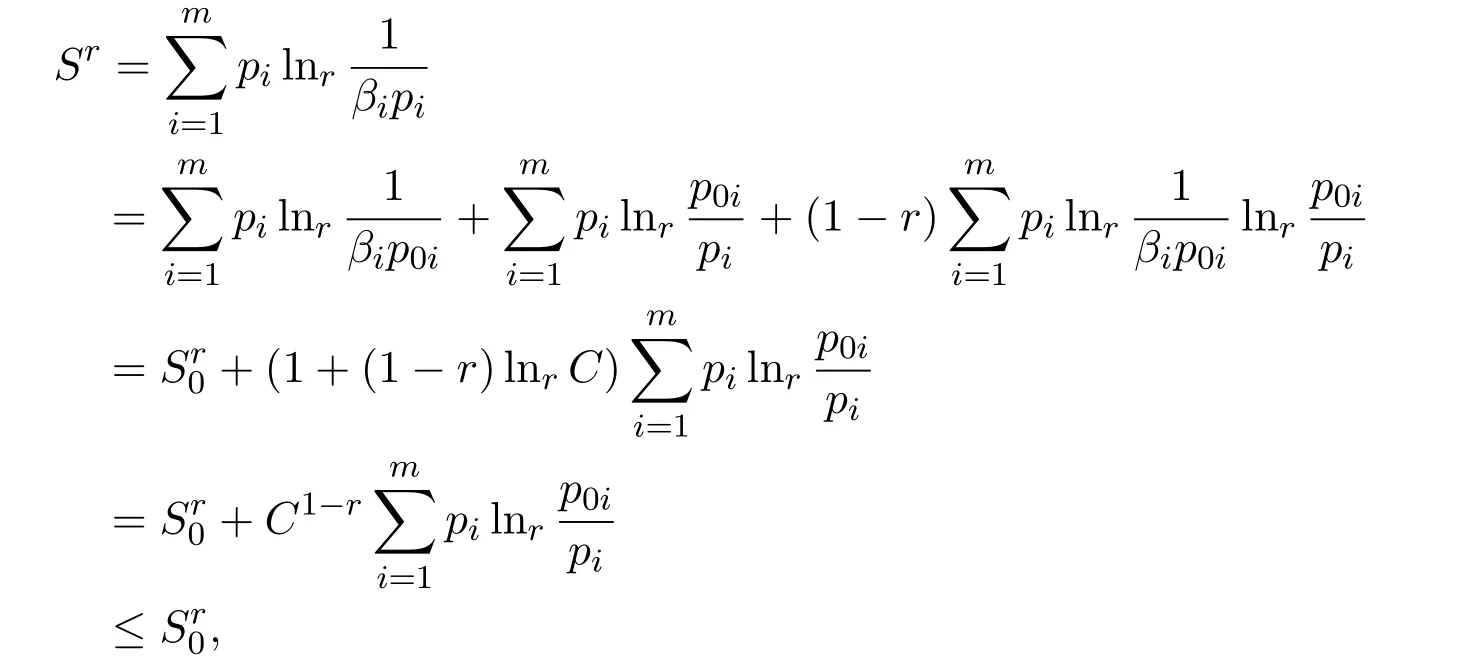
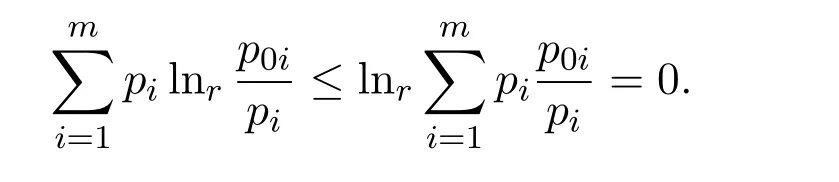
定理2.3假设,那么最大的Tsallis型非对称熵分布是

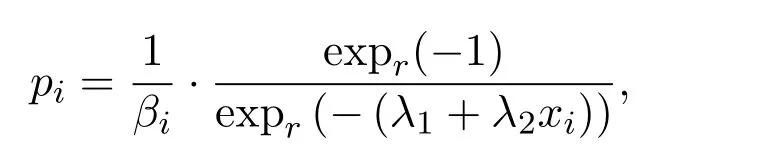
其中λ1和λ2满足两个约束条件:

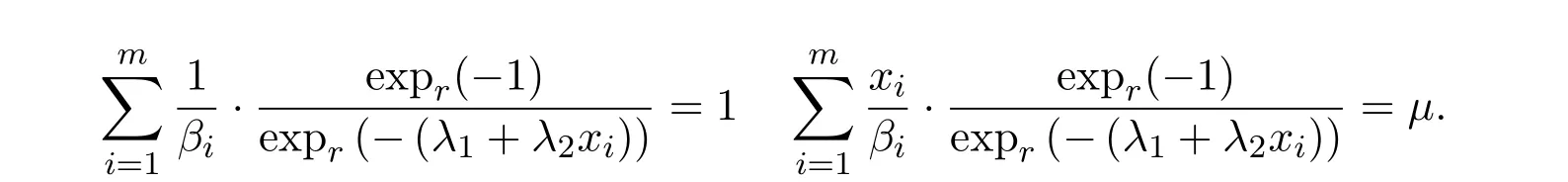
证明运用拉格朗日乘子法构造一个辅助函数:

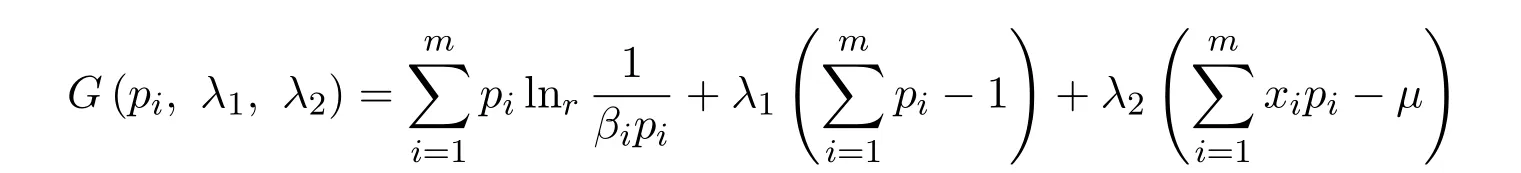
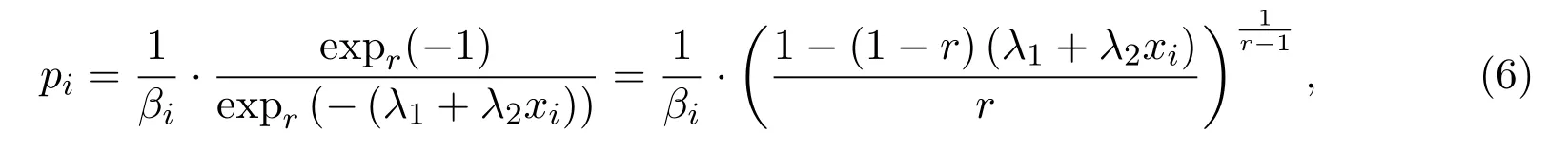
其中λ1和λ2满足两个制约条件

定理2.4 (在约束条件下的最大的Tsallis型非对称熵原理)Tsallis型非对称熵

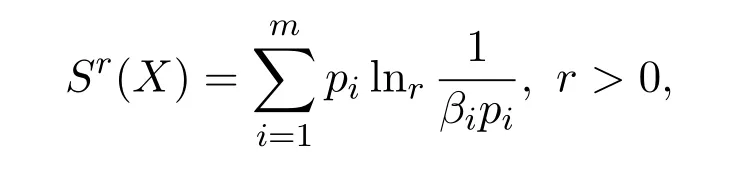
在n+1个约束条件,r=1,2,···,n下的最大熵分布为

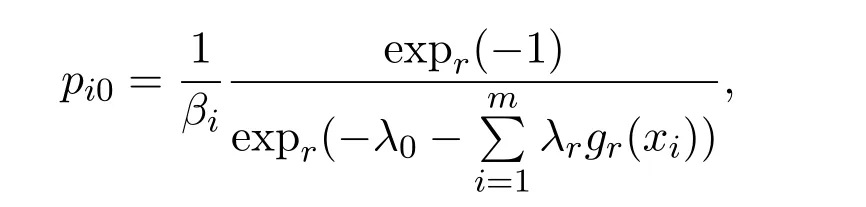
其中λ0和λ1(1≤i≤n)满足n+1个约束条件:

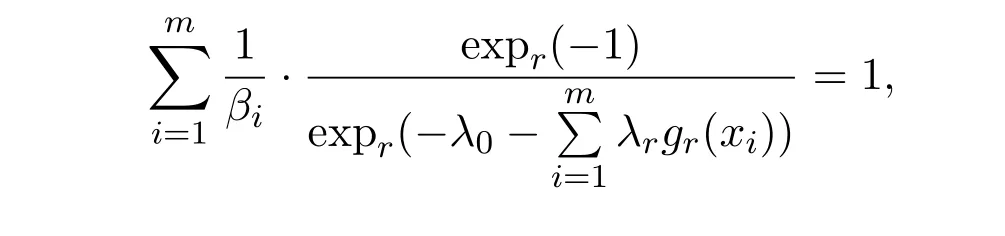
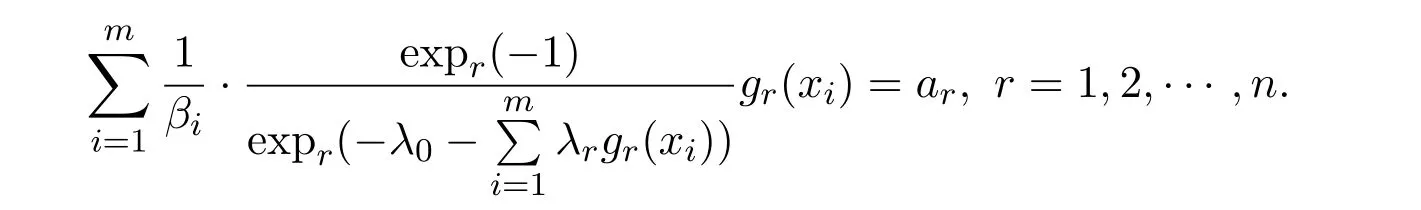
证明构造辅助函数

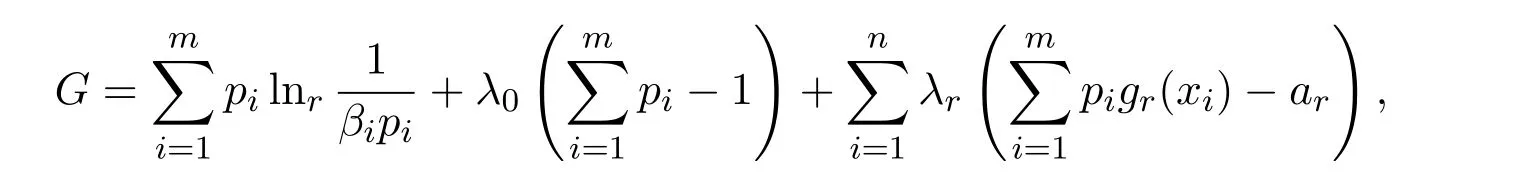
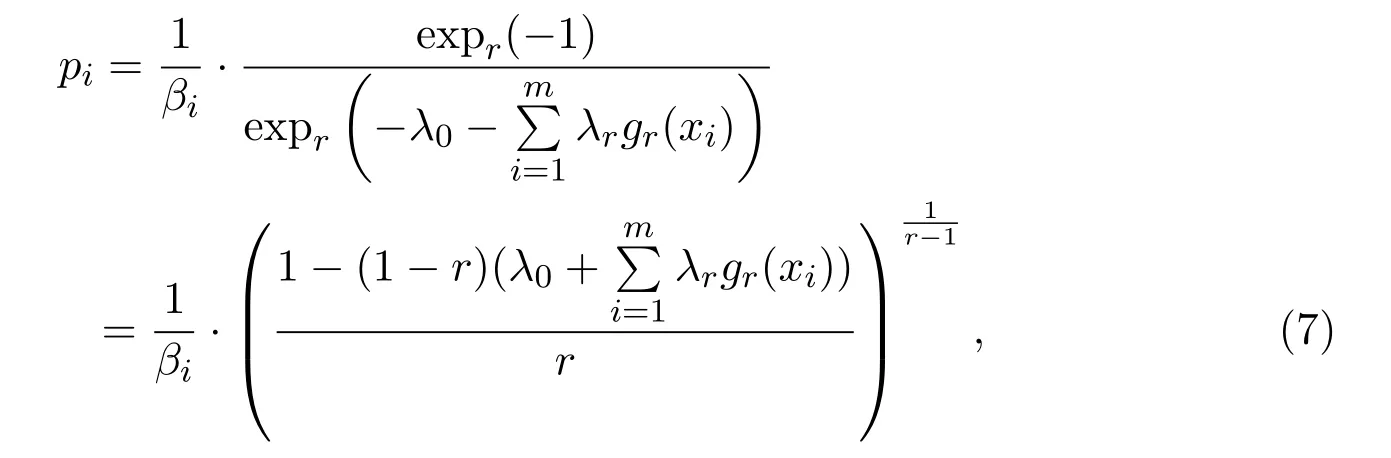
其中λ0,λ1,···,λn是拉格朗日乘子.

定义2.3 对于连续的情况,Tsallis型非对称熵定义为:

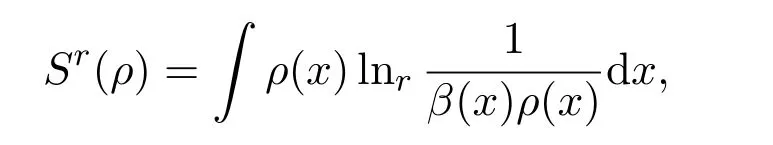
其中β(x)是辅助信息∫参数函数,ρ(x)是事件x的概率密度.

定理2.5 假设xρ(x)dx=µ,那么最大的Tsallis型非对称熵分布是

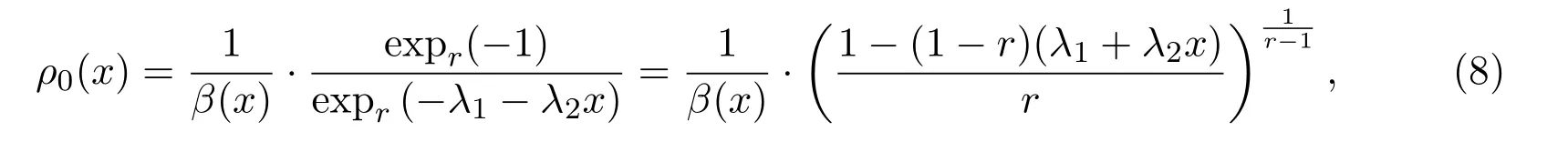
其中λ1和λ2满足两个约束条件:

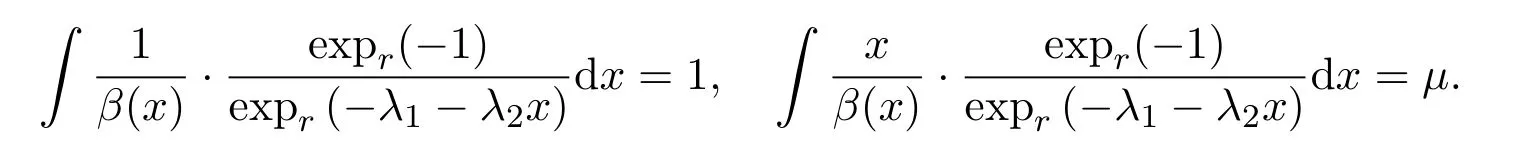
证明运用拉格朗日乘子法构造一个辅助泛函:

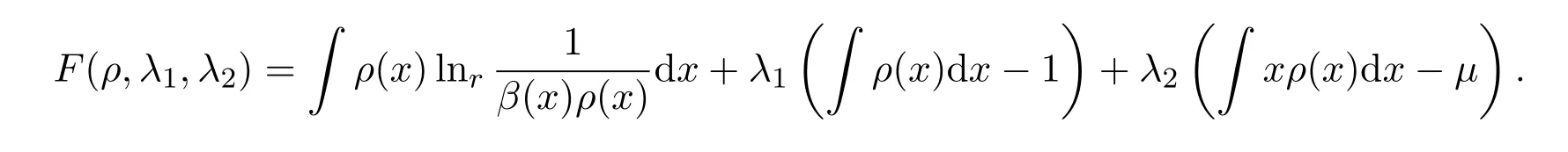
有

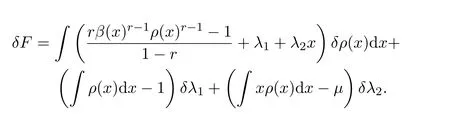
由δF=0,可以推出

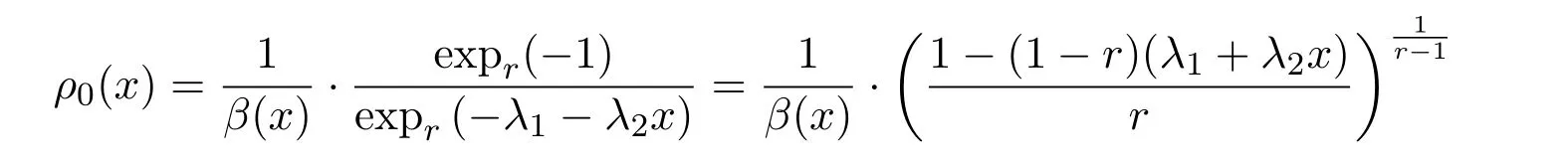
其中λ1和λ2满足两个制约条件

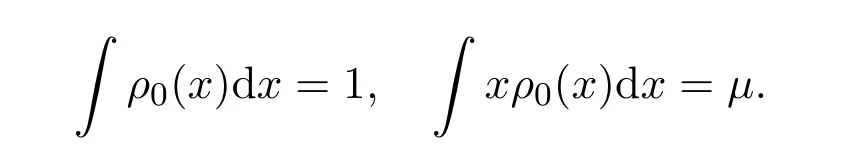
定理2.6 假设

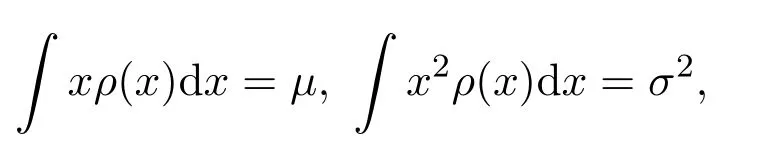
那么最大的Tsallis型非对称熵分布是

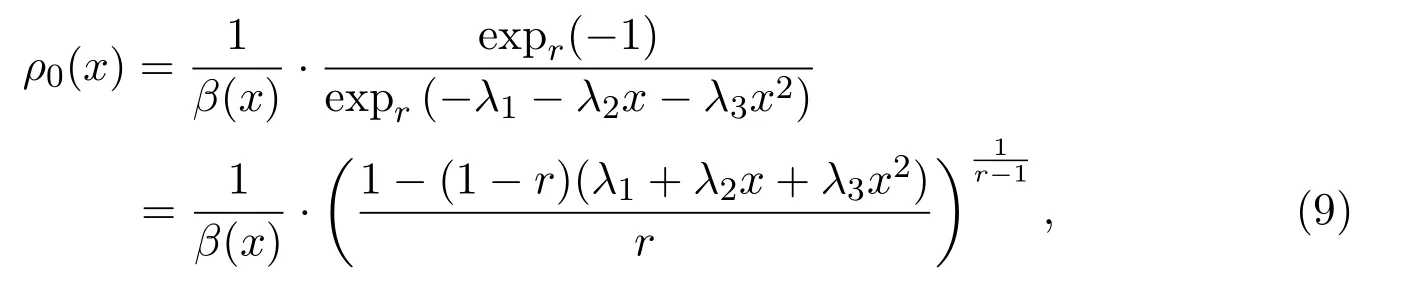
其中λ1,λ2和λ3满足 3个约束条件:

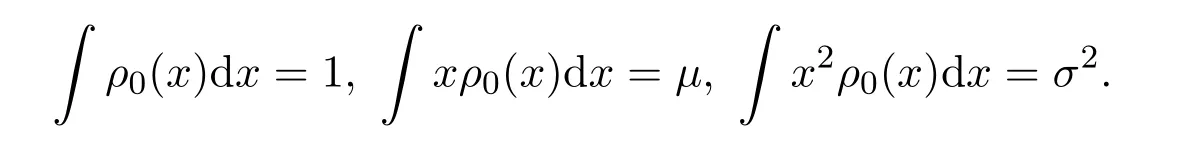
证明 运用拉格朗日乘子法构造一个辅助泛函:

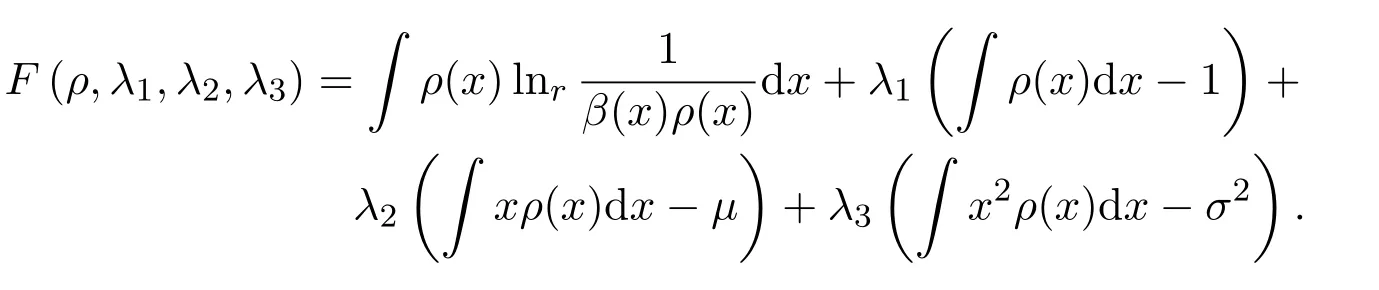
有

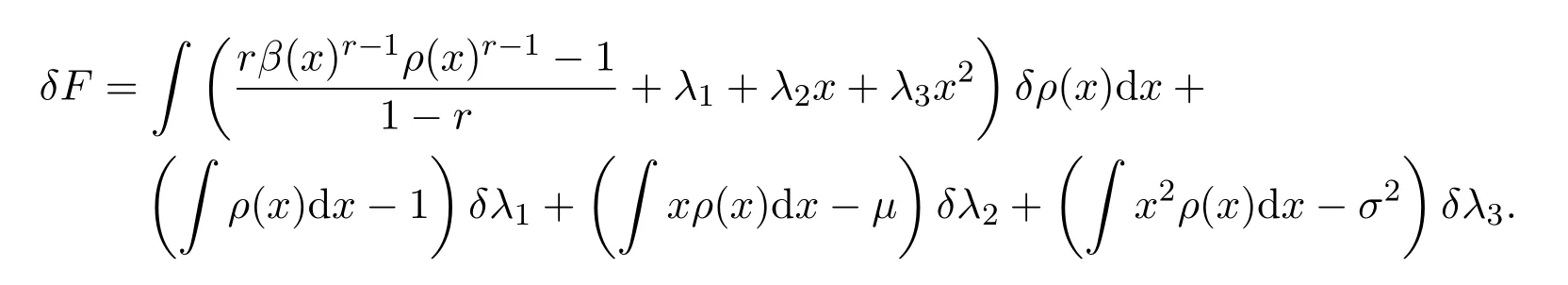
由δF=0,可以推出

其中λ1,λ2和λ3满足3个制约条件

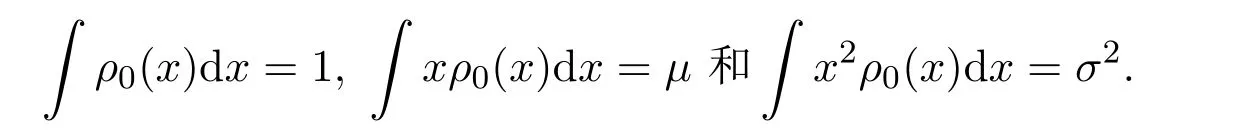
下面将离散情形下的最大的Tsallis型非对称熵原理推广到连续的情形.

定义2.4 令Λ是一类概率密度函数集,如果存在ρ0∈Λ,使得

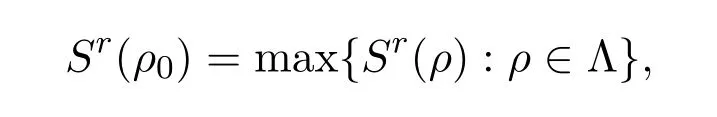
那么ρ0叫作最大的Tsallis型非对称熵的分布,Sr(ρ0)叫做最大的 Tsallis型非对称熵.

定理2.7 (连续情形下的最大的 Tsallis型非对称熵原理)令 Λ是一类固定的概率密度函数,如果存在ρ0∈Λ,使得,对于任意的ρ而言,它是一个与ρ(x)无关的常数.那么ρ(x)是最大的 Tsallis型非对称熵的分布,Sr(ρ0)=S0=lnrC是最大的Tsallis型非对称熵.

证明对于任意的ρ∈Λ,有

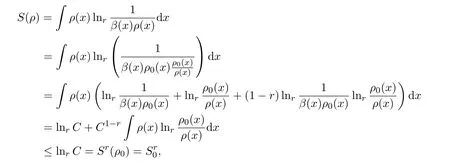
3 应用

利用(6)式-(9)式,可以得到许多特殊的分布.例如,在(8)式中,令