HilbertC∗-模中K-框架的对偶性
相中启,石黄萍
(上饶师范学院数学与计算机科学学院,江西 上饶334001)
1.引言
Hilbert空间中框架(经典框架)概念的出现可以追溯到上世纪50年代[1],当时它被用来处理非调和Fourier数中的一些深刻问题.1986年,Daubechies等[2]重新引入并进一步发展了框架理论,他们的开创性工作使得沉寂了30多年的框架理论再次进入人们的视野并引起了广泛关注.因许多好的性质,目前框架已在理论和应用领域中发挥着重要的作用,更多详情参看文[3-9].在研究算子的原子分解时,G˘avrut¸a[10]引入了K-框架的概念.由文[11-14]可知,尽管K-框架是框架的推广,但是由于有界线性算子K的制约,其性质几乎完全不同于框架.
最近,K-框架的概念被推广到了HilbertC∗-模中[15−16].虽然HilbertC∗-模是Hilbert空间的一般化,但是由于二者之间的一些本质差异(比如HilbertC∗-模中的闭子模未必正交可补;其上存在不可伴的有界算子,等),HilbertC∗-模上的C∗-代数的复杂性以及Hilbert空间中的一些有用的技巧不再适用于HilbertC∗-模,致使HilbertC∗-模中的K-框架问题要比Hilbert空间情形复杂很多,所以K-框架理论由Hilbert空间到HilbertC∗-模的推广工作并非平凡.
由于框架算子一般不可逆,所以HilbertC∗-模中的K-框架没有经典的典范对偶,这导致其对偶性问题研究起来相当困难,关于这方面的成果很少.本文从新的角度刻画了HilbertC∗-模中K-框架的对偶性.首先给出HilbertC∗-模中的序列成为给定K-框架的K-对偶Bessel序列的充分必要条件; 其次得到K-对偶Bessel序列的等价条件,使得K-框架及由其K-对偶Bessel序列诱导的Bessel序列可以在一个闭子模上交换位置; 最后给出条件使得给定K-框架存在唯一的、其解析算子取得最小范数的K-对偶Bessel序列,这为寻求HilbertC∗-模中K-框架的典范对偶的定义方式提供了一些思路.
2.准备工作
本节回顾一些记号、定义及下节所要用到的一些结果.
全文采用如下记号:A表示有单位元的C∗-代数,J有限或可数指标集.用F,H和K表示A上的有限或可数生成HilbertC∗-模,End∗A(H ,K)表示H到K的可伴算子的全体,End∗A(H ,H)缩写为End∗A(H).
定义2.1[15]设K ∈End∗A(H),{fj}j∈J是H中的序列,若存在常数C,D >0使得

则称{fj}j∈J是H的K-框架,C,D分别称为{fj}j∈J的下、上K-框架界.如果只有(2.1)右侧的不等式成立,则称{fj}j∈J是H的Bessel序列,D称为Bessel界.
设K ∈End∗A(H),{fj}j∈J是H中的序列,如果

则称{fj}j∈J是H的ParsevalK-框架.
由(2.2)易推知

设{fj}j∈J是H的Bessel序列,其解析算子定义为:

其中ℓ2(A)是由下式定义的A上的HilbertC∗-模:

易见,U的伴随算子由下式给出:

下面的定义是文[12]中定义2.5的推广.
定义2.2设K ∈End∗A(H),{fj}j∈J是H的K-框架,又设{gj}j∈J是H的Bessel序列.如果

则称{gj}j∈J是{fj}j∈J的K-对偶Bessel序列.
引理2.1[17]设Λ ∈End∗A(H ,K)有闭的值域,则存在Λ的Moore-Penrose逆Λ†∈End∗A(K ,H)使得
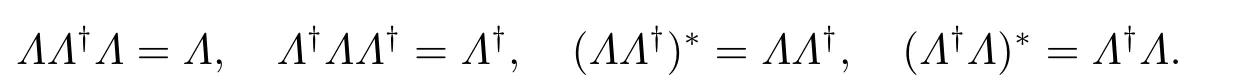
引理2.2[18]设T′∈End∗A(H ,F),T ∈End∗A(K ,F),且设正交可补,则以下论断等价:
1) 对某个λ>0,有T′T′∗≤λTT∗.
2) 存在µ>0使得任意z ∈F,∥T′∗z∥≤µ∥T∗z∥.
3) 存在S ∈End∗A(H ,K)使得T′=TS,即TX=T′有解.
4) Range(T′)⊆Range(T).
此外,存在唯一的S满足T′=TS以及Range(S)⊆(KerT)⊥.此时有

引理2.3[19]序列{fj}j∈J是H的界为D的Bessel序列当且仅当
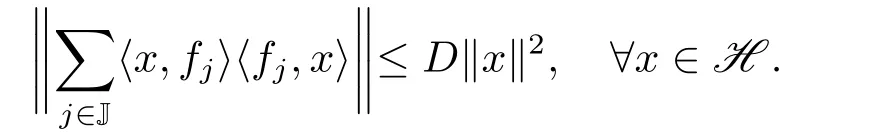
为了表述的方便,下文中Df和Uf分别用来表示Bessel序列{fj}j∈J的Bessel界和解析算子.进一步,如果{fj}j∈J是K-框架,则用Cf表示其下K-框架界.
3.主要结果
本节给出HilbertC∗-模中K-对偶Bessel序列的一些刻画,首先有
定理3.1设K ∈End∗A(H),{fj}j∈J是H的K-框架,则序列{gj}j∈J⊂H是{fj}j∈J的K-对偶Bessel序列当且仅当存在φ ∈End∗A(H ,ℓ2(A)),使得K=U∗fφ以及任意j ∈J有gj=φ∗ej,其中{ej}j∈J是ℓ2(A)的标准正交基.
证首先设{gj}j∈J是{fj}j∈J的K-对偶Bessel序列,则由(2.6)知K=U∗fUg.令φ=Ug,则K=U∗fφ.因为对任意x ∈H有所以

于是φ∗ej=U∗gej=gj,∀j ∈J.
反过来,对任意x ∈H可得

由引理2.3 知{gj}j∈J是H的界为∥φ∥2的Bessel序列.又
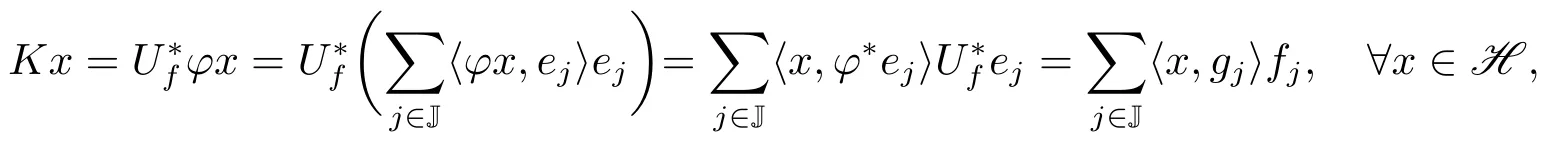
因此{gj}j∈J是{fj}j∈J的K-对偶Bessel序列.
易见(2.6)中{fj}j∈J和{gj}j∈J的位置一般不可交换(除非K自伴),但是如下关于K-对偶Bessel序列的充分必要条件表明,如果K有闭的值域,则{fj}j∈J和由{gj}j∈J诱导的Bessel序列可以在Range(K)上交换位置.
定理3.2设K ∈End∗A(H)有闭的值域,又设{fj}j∈J是H的K-框架,{gj}j∈J是H中的序列,那么以下论断等价:
1){gj}j∈J是{fj}j∈J的K-对偶Bessel序列.

证1)⇒2).任意z ∈KerK,由K-对偶Bessel序列的定义知

任意z ∈Range(K),联合(2.6)和引理2.1得

任意j ∈J,令hj=(K†|Range(K))∗gj,则对任意x ∈H有

由引理2.3,{hj}j∈J是H的界为Dg∥K†∥2的Bessel序列.现在,任意y,z ∈Range(K),

2)⇒1).因为Range(K†)=(KerK)⊥,所以每个x ∈H可表示为x=x1+x2,其中x1∈Range(K†),x2∈(Range(K†))⊥=KerK.由引理2.1,K†K是Range(K†)上的正交投影,所以由(3.1)知


这表明{gj}j∈J是{fj}j∈J的K-对偶Bessel序列.
一般地,K-对偶Bessel序列并不是K-框架.但是如果附加一些条件,则K-对偶Bessel序列可自然生成K-框架
定理3.3设K ∈End∗A(H)有闭的值域,{fj}j∈J是H的K-框架,{gj}j∈J是其K-对偶Bessel序列.如果正交可补,则{Kgj}j∈J是H的K-框架.
证对任意x ∈H有于是

因此

由于K有闭的值域,故K∗也有闭的值域.所以任意y ∈Range(K∗),由引理2.1知y=K∗(K∗)†y=K†Ky,从而∥y∥2=∥K†Ky∥2≤∥K†∥2∥Ky∥2.于是
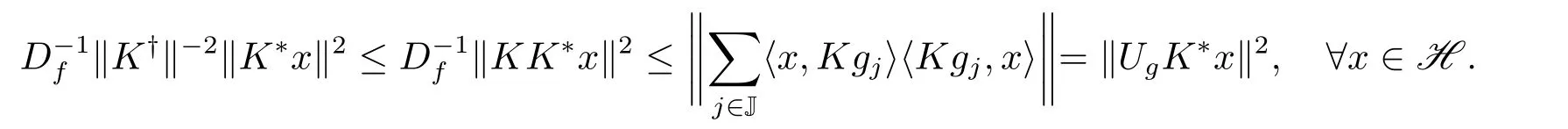
由引理2.2,存在λ>0使得KK∗≤λ(UgK∗)∗(UgK∗).故

这就完成了证明.
HilbertC∗-模上K-框架的K-对偶Bessel序列可能不唯一,请检查下面的例子.
例3.1设ℓ∞是所有有界复值序列的集合.任意u={uj}j∈N,v={vj}j∈N∈ℓ∞,定义

则A={ℓ∞,∥·∥}是一C∗-代数.
设H=C0是收敛于零的序列的全体.任意u,v ∈H,定义那么H是A上的HilbertC∗-模.
设{ej}j∈N是H的标准正交基且定义映射K:H →H如下:Ke1=e1,Ke2=e1,Kej=ej,j ≥3.
容易验证K ∈End∗A(H).任意j ∈N,令fj=Kej,则对任意x ∈H有

所以

说明{fj}j∈N是H的ParsevalK-框架.由(3.2)可推知这表明{gj}j∈N={ej}j∈N是{fj}j∈N的K-对偶Bessel序列.令

简单计算可知{hj}j∈N是H的Bessel序列.任意x ∈H,因为

所以{hj}j∈N是{fj}j∈N的K-对偶Bessel序列且
接下来的结果表明,HilbertC∗-模中给定K-框架的两个K-对偶Bessel序列之间的差别可视为一个可伴算子.
定理3.4设K ∈End∗A(H),{fj}j∈J是H的K-框架,{gj}j∈J是其K-对偶Bessel序列.那么序列{hj}j∈J⊂H是{fj}j∈J的K-对偶Bessel序列当且仅当存在φ ∈End∗A(H ,ℓ2(A))使得任意j ∈J和x ∈H,有U∗fφ=0,⟨x,hj−gj⟩=(φx)j.
证首先设{hj}j∈J是{fj}j∈J的K-对偶Bessel序列.定义映射φ:H →ℓ2(A),(φx)j如下:

则φ ∈End∗A(H ,ℓ2(A)).事实上,任意{cj}j∈J∈ℓ2(A)有


反过来,对任意x ∈H有


所以{hj}j∈J是{fj}j∈J的K-对偶Bessel序列.
下面的结果表明,一定条件下给定K-框架的所有K-对偶Bessel序列中存在唯一的K-对偶Bessel序列,其解析算子取得最小范数.
定理3.5设K ∈End∗A(H),{fj}j∈J是H的K-框架且Range(Uf)正交可补,则存在唯一的{fj}j∈J的K-对偶Bessel序列{gj}j∈J满足且使得对{fj}j∈J的任意K-对偶Bessel序列{hj}j∈J有∥Ug∥≤∥Uh∥.
证任意x ∈H,因为


任意j ∈J,令gj=S∗ej,其中的标准正交基.那么任意x ∈H,

所以{gj}j∈J是H的界为∥S∥2的Bessel序列.任意j ∈J,因为U∗fej=fj,故

说明{gj}j∈J是{fj}j∈J的K-对偶Bessel序列.又任意x ∈H,

因此Ug=S,进一步有现在设{hj}j∈J是{fj}j∈J的任一K-对偶Bessel序列,则K=U∗fUh,于是K∗=U∗hUf.任意x ∈H,因为

所以∥Ug∥2=∥S∥2≤∥Uh∥2,这等价于∥Ug∥≤∥Uh∥.
有趣的是,ParsevalK-框架可以自然生成自身的K-对偶Bessel序列.特别地,如果K有闭的值域,则该K-对偶Bessel序列取得最小范数.
定理3.6设K ∈End∗A(H)有闭的值域,{fj}j∈J是H的ParsevalK-框架,则{K†fj}j∈J是{fj}j∈J的K-对偶Bessel序列,且对{fj}j∈J的任意K-对偶Bessel序列{gj}j∈J有∥Ug∥≥∥U′f∥,其中U′f是{K†fj}j∈J的解析算子.
证因为{fj}j∈J是一ParsevalK-框架,则易于验证{K†fj}j∈J是H的Bessel序列且对任意x ∈H有由引理2.1 得

故{K†fj}j∈J是{fj}j∈J的K-对偶Bessel序列.现在设{gj}j∈J是{fj}j∈J的任一K-对偶Bessel序列,则任意x ∈H,
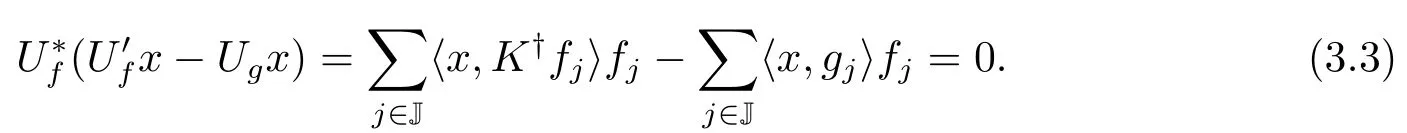
因为U′fx={⟨x,K†fj⟩}j∈J={⟨(K†)∗x,fj⟩}j∈J=Uf(K†)∗x,所以U′f=Uf(K†)∗.这与(3.3)一起得到

因此(U′f)∗(U′f−Ug)x=0,这等价于(U′f)∗U′f=(U′f)∗Ug.于是

由此可知∥U′f∥≤∥Ug∥.

