关于有限群p－超可解性与p－幂零性的新判定

陈德平， 尤 泽， 李保军

(成都信息工程大学应用数学学院，四川成都610225)

本文所研究的群皆为有限群，用G表示一个群，|G|表示群G阶，π(G)为|G|的所有素因子的集合，p为一个素数．文中所用符号和概念大多是标准的，未指明的符号和概念可参见文献［1－2］．

群G的子群H与T称为可置换的，如果HT=TH．已知群G的2个子群的乘积仍为子群的充要条件是它们可置换(参见文献［1］的定理1．2)．因此，子群的可置换性为子群的一个重要性质．一个群的正规子群与其所有子群可置换，但反之不然．若群G的子群H与G的所有子群可置换，则称H为G的拟正规子群［3］或置换子群［4］．推广这一概念，群 G的子群H被称为为s－置换子群(或s－拟正规子群)［5－6］，如果 H 与 G 的所有 Sylow 子群可置换．s－置换子群与置换子群有着很多相近的性质，如s－置换子群也是次正规子群以及无核s－置换子群幂零等．近年来，在对置换子群和s－置换子群研究的基础上，一些新的子群广义置换性质被提出并得到了较为广泛的研究，譬如 Guo 等［7－8］对 X－置换子群和c－置换子群的研究;Wang 等［9－10］对 c－正规子群和c－可补子群的研究等．这些广义置换子群也有着很好的性质并深刻的影响着群结构，文献［11］得到群G的无核X－置换子群(其中X为G的某一正规幂零子群)为超可解子群;文献［9］证明所有极大子群皆为c－正规的群一定可解．利用子群各类广义置换性质研究群结构的最为广泛的研究工作是通过极小子群和Sylow子群的极大子群刻画群结构［12－16］．统一和发展这方面的研究．2007 年，Skiba［17］提出了弱s－置换子群的概念，并利用这一概念，给出了一些有意义的研究成果．本文主要研究工作为利用某些子群的弱s－置换性质研究群的p－超可解性和p－幂零性，将得到一些关于群结构的新刻画．

1 预备知识

首先列出一些文中将会用到的基本概念和引理．

定义 1．1［5］群G的一个子群H在G中称为s－置换的，若对G阶的任意素因子p和G的任意Sylow p－子群 P，都有 HP=PH．

由定义所有正规子群和置换子群都是s－置换的．根据文献［16］中的引理 2．1(5)的证明，容易得到2个s－置换子群的交还是s－置换的．设H、K为G的2个子群，由于G有限，〈H，K〉一定可分解为有限多个H与K的乘积．因此，如果H与K都是s－置换的，则〈H，K〉也是．

定义 1．2［17］群G的一个子群H在G中称为弱s－置换的，如果G中存在一个次正规子群T，使得HT=G且T∩H≤HsG，其中HsG为含于H的G的最大s－置换子群．

对弱s－置换子群，有以下基本性质:

引理 1．3［17］设 H≤K≤G，则有

1)如果H在G中s－置换，则H在G中是弱s－置换的;

2)假设H是群G的正规子群，则K/H在G/H中弱s－置换当且仅当K在G中也是弱s－置换的;

3)如果H在G中弱s－置换，则H在K中也弱s－置换;

4)假设H是群G的正规子群，若在G中弱s－置换的子群E满足(|H|，|E|)=1，则商群HE/H在G/H中也弱s－置换．

引理 1．4 设H是群G的s－置换子群，P是G的一个 p－子群．若 p|H|，则 P≤NG(H)，进而有Oπ(G)≤N(H)，其中π ={p∣ p|H|}．

G

证明 设Gp为G的包含P的一个Sylow p－子群．因为H是群G的s－置换子群，所以HGp=GpH为G的一个子群．由p|H|知H为HGp的一个Hall子群．另一方面，由于s－置换子群必为次正规子群，得到H次正规于HGp．但次正规的Hall子群必然正规，因此HHGp．于是 P≤Gp≤NG(H)．由 P 的任意性，立即可以得到Oπ(G)=〈P∣P为准素子群且(|P|，|H|)=1〉≤NG(H)．

引理1．5 设G有唯一极小正规子群N．若N为初等交换 p－群且 N ≤/Φ(G)，则

N=Op(G)=F(G)=CG(N)．证明 因为N≤/Φ(G)，所以存在G的极大子群M使得N≤/M．因此G=NM．由N交换，N∩MNM=G．但N极小正规子群，因此N∩M=1．又由N为初等交换 p－群，显然有 N∈Op(G)∈F(G)∈CG(N)．设 C=CG(N)，则

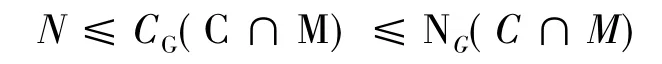
2 主要结果

定理2．1 设G为p－可解群．若对于G的任一非Frattini p－主因子 H/K，存在G的 Sylow p－子群的极大子群P1不覆盖H/K且在G中弱s－置换，则G是p－超可解的．

证明 假设定理不成立，并设G是一个极小阶反例．通过以下步骤完成证明．

1)Op'(G)=1．若Op'(G)≠1，假设 N 是包含在Op'(G)中G的极小正规子群．下面考虑商群G/N．设(H/N)/(K/N)为G/N的任一非Frattini p－主因子，则H/K为G的一个非Frattini p－主因子．由条件，存在G的Sylow p－子群的极大子群P1不覆盖H/K且在G中弱s－置换．显然，P1N/N为G/N的一个Sylow子群的极大子群．又由HP1K有

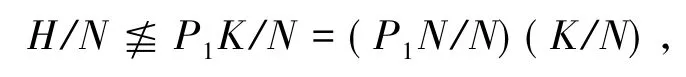
所以P1N/N不覆盖 H/N/K/N．又因为 N为 p'－子群，由引理1．3的 4)，有 P1N/N 在 G/N 中弱 s－置换．因此条件对G/N成立．又由G的极小性有G/N是p－超可解的，故G也是p－超可解的，矛盾．

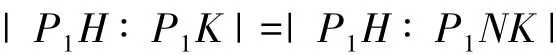
为 p'－数．另一方面|P1H ∶P1K|||H ∶K|为 p－数．因此|P1H ∶P1K|=1，即 P1H=P1K，矛盾．所以 N≤P1．由引理1．3的2)，P1N/N在G/N中是弱s－置换的．显然P1N/N不覆盖(H/N)/(K/N)，因此条件对G/N成立．于是G/N是p－超可解的．若G中包含不同于N的极小正规子群M，则N∩M=1，因此GG/M∩N为p－超可解，矛盾．所以N是G的唯一极小正规子群．又若N≤Φ(G)，则由p－超可解群的群类是一个饱和群系，可知G为p－超可解，因此NΦ(G)．由引理 1．5 有3)最后的矛盾．设N为G的极小正规子群，由2)，N是初等交换p－群且NΦ(G)．故能找到一个G的Sylow p－子群的极大子群P1，使得NP1且P1在G中弱s－置换，即存在LG，使得P1L=G且P1∩L≤P1sG．由N是G的唯一极小正规子群，有N≤Op(G)≤L．若不然 Op(G)=1，即 G 是p－群，矛盾．于是P1∩N=P1∩L∩N=P1sG∩N 在 G 中是 s－置换的．因此由引理1．4有

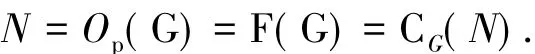
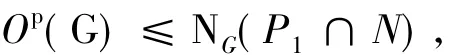
设Gp为包含P1的G的Sylow p－子群，由P1是Gp的极大子群，有 P1Gp．又 NGp，所以 P1∩NGp，因此 G=OP(G)Gp≤NG(P1∩N)，即 P1∩NG．但是 NP1且N为极小正规子群，因此P1∩N=1．于是|Gp|=|N||P1|，所以|N|=p．由 G/N 是 p－超可解，N是p阶的，说明了G也是p－超可解的．这一最后矛盾表明定理成立．

注 2．1 定理2．1中G为p－可解群的条件不可去掉．事实上，设G为5次交错群A5，则G的Sylow 3－子群的极大子群都为1，从在A5内是弱s－置换的，但显然A5不是3－超可解的．

定理2．2 设p是群 G阶的素因子且(p－1，|G|)=1．若对于G的任一非Frattini p－主因子H/K，存在G的Sylow p－子群的极大子群P1不覆盖H/K且在G中弱s－置换，则G是p－幂零的．

证明 假设定理不成立，并设G是一个极小阶反例．通过以下步骤完成证明．

1)Op'(G)=1．若Op'(G)≠1，假设 N 是包含在Op'(G)中G的极小正规子群．下面考虑商群G/N，设(H/N)/(K/N)为G/N的任一非Frattini p－主因子，则H/K为G的一个非Frattini p－主因子．由条件，存在G的Sylow p－子群的极大子群P1不覆盖H/K 且在 G 中弱 s－置换．由引理1．6，P1N/N 为 G/N的一个Sylow子群的极大子群．由HP1K有H/NP1K/N=(P1N/N)(K/N)，所以 P1N/N不覆盖(H/N)/(K/N)．又因为 N 为 p'－子群，由引理 2．3的4)，有P1N/N在G/N中弱 s－置换．因此条件对G/N成立．又由G的极小性有G/N是p－幂零的，故G也是p－幂零的，矛盾．

2)G的极小正规子群N是p－群．设N是G的任意极小正规子群，由1)知，N 是一个 pd－群．若p2N，则N为p－幂零的，由N的极小性且Op'(G)=1，知N是p－群．又若N≤Φ(G)，则N显然为p－群．设p2N且NΦ(G)，由定理条件，存在G的Sylow p－子群的极大子群P1在G中弱s－置换，即存在LG，使得P1L=G且P1∩L≤P1sG．若 N 不是 p－群，则 N=Op(N)≤Op(G)≤L，所以

P1∩N=P1∩L∩N=P1sG∩N

在G中是s－置换的，因此由引理1．4，可得P1∩N≤Op(G)．由 p2|N，P1∩N≠1，从而

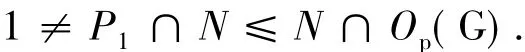
于是N≤Op(G)，此矛盾说明2)成立．

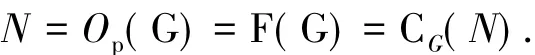
设N是G的任意极小正规子群，由2)知，N为一个p－群．设(H/N)/(K/N)为G/N的任一非Frattini p－主因子，则H/K为G的一个非Frattini p－主因子．设P1不覆盖 H/K，即 P1H≠P1K．若 NP1，则 NP1为G的一个Sylow p－子群．因此

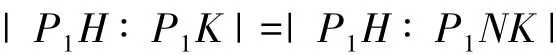
为 p'－数．另一方面|P1H ∶P1K|||H ∶K|为 p－数．则|P1H ∶P1K|=1，即 P1H=P1K，矛盾．所以N≤P1．又显然有P1N/N不覆盖(H/N)/(K/N)并且根据引理1．3的2)，可得定理条件G/N仍成立．由G的极小性，G/N是p－幂零的．若G中包含不同于N的极小正规子群M，则N∩M=1，因此GG/M∩N为p－幂零，矛盾．所以N是G的唯一极小正规子群．又若N≤Φ(G)，则由p－幂零群的群类是一个饱和群系，可知G为 p－幂零群，因此 NΦ(G)．由引理 1．5，N=Op(G)=F(G)=CG(N)成立．

4)最后的矛盾．设N为G的极小正规子群，由3)，N是初等交换p－群且NΦ(G)．故能找到一个G的Sylow p－子群的极大子群P1，使得NP1且P1在G中弱s－置换．即存在LG，使得P1L=G且P1∩L≤P1sG．由N是G的唯一极小正规子群，有N≤Op(G)≤L．若不然 Op(G)=1，即 G 是p－群．于是 P1∩N=P1∩L∩N=P1sG∩N在G中是s－置换的，因此由引理 1．4 有

设Gp为包含P1的G的Sylow p－子群，由 P1是 Gp的极大子群，有 P1Gp．又 NGp，所以 P1∩NGp，因此 G=OP(G)Gp≤NG(P1∩N)，即 P1∩NG．但是NP1且N为极小正规子群，因此P1∩N=1，于是|Gp|=|N||P1|，所以 |N|=p．由 N/C 定理，G/CG(N)同构于Aut(N)一个子群．因此但由条件(|G|，p－1)=1，因此 G/CG(N)=1．再由G/N是p－幂零，有G是p－幂零的．

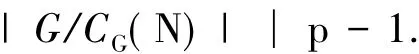
推论2．3 设p是群G阶的任意一个素因子．若对于G的任一非Frattini p－主因子H/K，存在G的Sylow p－子群的极大子群P1在G中弱s－置换且H/KP1K/K，则G是超可解的．

证明 设p是群G阶的极小素因子，必然有(p－1，|G|)=1，由定理 2．2 以及 Feit－Thompson 奇

阶群可解定理，知G是可解的．再由定理2．1，对于 任意素数p，G是p－超可解的，因此G为超可解．