基于UKF-GM-PHD滤波算法的非线性多目标跟踪方法研究*
齐海明 张安清
(1.海军91648部队 葫芦岛 125004)(2.海军大连舰艇学院信息系统系 大连 116018)
1 引言
目前,基于PHD滤波的多目标跟踪方法研究已成为目标跟踪领域的热点。PHD滤波[1]可以更好地反映出目标跟踪问题的本质,以集合形式描述多目标跟踪问题,同时可以描述跟踪过程中目标的新生、消失和衍生等情况,即可完成目标的状态估计,也可以实现目标的数目估计,避免了数据关联的难题,受到国内外众多学者的关注。
PHD 滤波算法[2~5]是一种基于有限集统计学(Finite Set Statistics,FISST)的次最优多目标Bayes滤波器,但该方法在进行迭代运算时存在多重积分,仍需要采取数值计算的方法来实现近似。Vo基于线性高斯假设条件,利用高斯混合技术提出了高斯混合PHD(GM-PHD)滤波器[6],同时在理论上证明该滤波器存在闭合解。GM-PHD滤波器计算量较小,并且状态估计峰值提取相对容易,工程易实现。而现实情况中目标跟踪问题很多是非线性的,因此,如何实现GM-PHD滤波器的非线性目标跟踪问题一直是研究的重点和难点。本文基于GM-PHD滤波算法在进行预测和更新过程中,是基于Kalman滤波原理,提出将传统非线性处理方法UKF与GM-PHD滤波算法相结合,提出UKF-GM-PHD算法,实现GM-PHD算法在非线性系统的应用。
2 PHD滤波器
PHD滤波器[7]实际是Bayes滤波器在随机有限集理论的推广,与传统Bayes滤波一样,分为预测步和更新步。
1)预测方程:
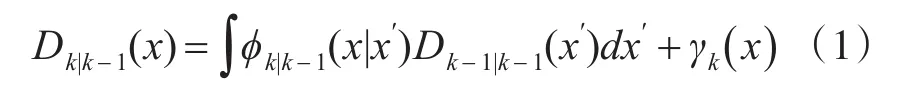
其中,Dk|k-1(x)代表多目标状态后验密度pk|k-1(Xk|Z1:k-1)的PHD函数,x和x′分别是k时刻和k-1时刻单目标状态。
2)更新方程:
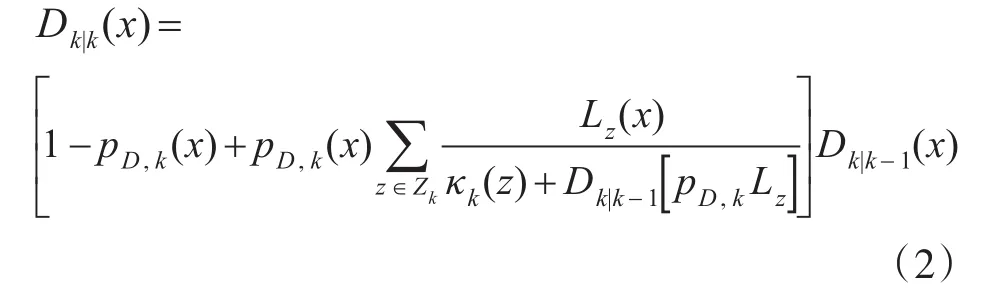
Lz(·)代表单目标量测似然函数,κk(·)为杂波量测的PHD。
与Bayes滤波算法递推公式一样,目标数目估计为[8]
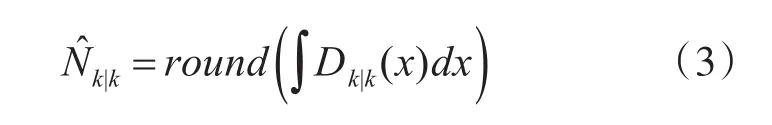
Dk|k(x)的N̂k|k个峰值对应的状态x即为目标集的状态估计x̂。由此可知,PHD滤波算法与传统目标跟踪算法不同,避免了复杂的数据关联过程,可同时实现对多个目标状态和目标数目的双重估计。
3 GM-PHD滤波器
GM-PHD滤波器为了得到闭合解,除了PHD滤波器的假设条件外,还需要以下假设[9~10]:
1)每个目标的Markov状态转移密度函数和目标量测似然函数均是线性高斯的;
2)目标存活概率PD,k()x和目标检测概率相互独立;
3)新生目标随机集Γk(·)PHD和衍生目标随机集Bk(·)PHD均是高斯混合的。
GM-PHD滤波器为了得到闭合解,在进行高斯分量迭代时是基于Kalman滤波原理,下面给出GM-PHD滤波算法的滤波流程:
预测过程:
k-1时刻的后验分布PHD高斯混合形式为
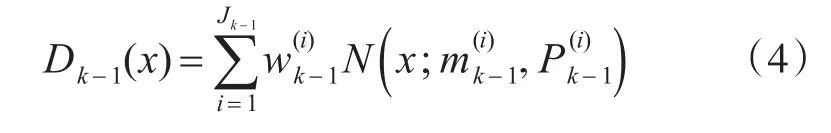
在文献[7]中Mahler已推导证明GM-PHD预测公式是三部分求和形式,公式表示为
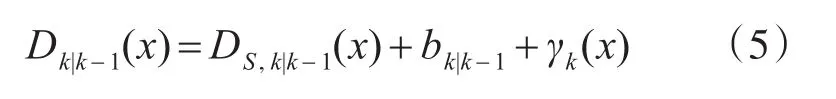
其中,DS,k|k-1(x),bk|k-1和γk(x)分别代表存活目标预测,衍生目标预测和新生目标预测PHD。
那么,k时刻的预测PHDDk|k-1(x)的高斯混合形式为
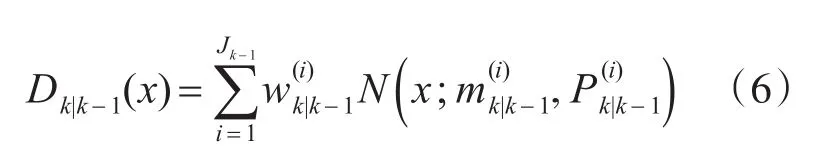
更新过程:
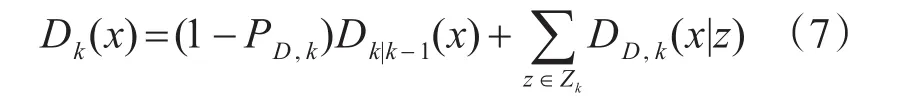
其中,第一部分是对漏检目标进行PHD更新;第二部分是对已检测目标进行PHD更新。
4 UKF-GM-PHD滤波器
在非线性目标跟踪系统中,系统的离线状态方程和量测方程为[11]
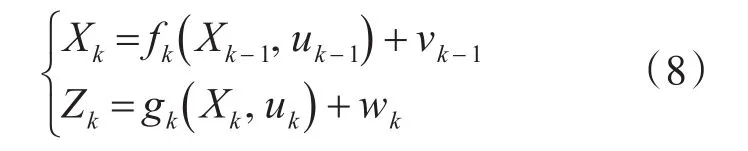
其中,fk和gk是非线性系统函数,uk为输入控制矩阵,vk-1是服从均值为零,协方差阵为Qk的正态分布过程噪声,wk是服从均值为零,协方差阵为Rk的正态分布量测噪声,且vk-1和wk相互独立。
4.1 UKF基本原理
UKF[12]是以Unscented变换(U变换)为基础,采用Kalman滤波原理,利用采样粒子逼近非线性函数。
U变换的原理:设x和y均为n维随机变量,满足非线性关系y=f(x),xˉ、yˉ和Px、Py分别是x和y的均值和协方差。选取一组采样点,确保采样点的均值与协方差不变,得到N个附带权值wi的sigma点χi,利用非线性函数关系获得每个采样sigma点对应的yˉ和Py。下面给出UKF的具体过程:
首先选取 2n+1个带有权值wi,i=0,1,…,2n的采样sigma点χi,根据非线性函数y=f(x),得到对应2n+1个yi,即:
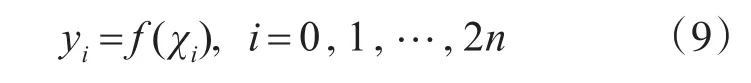
则yi对应的均值yˉ、协方差Py和互相关阵Pxy为
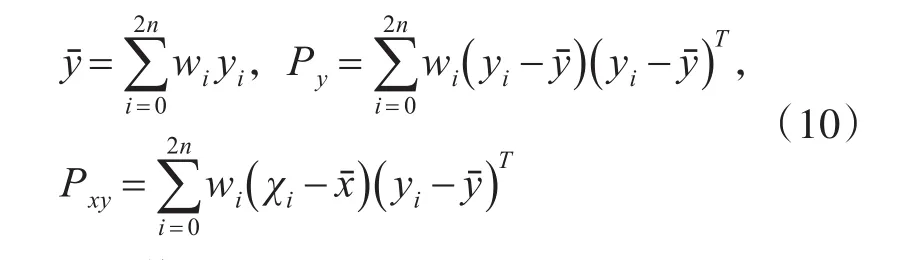
利用权值为wi的采样点χi对系统方程进行近似,将U变换原理用于非线性系统模型中,其中wi和采样点χi取值分别为
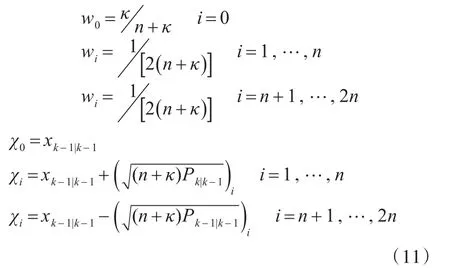
其中,κ为调整尺度参数,用于调整采样点与xˉ的距离,同时n+κ≠0,一般令为均方根矩阵(n+κ)Px的第i行。
由式(11)可得到状态预测值xk-1|k-1和协方差阵Pk|k-1,然后根据式(10)和(9),可得到量测值zk|k-1,新息协方差矩阵Pzz、互相关矩阵Pxz、状态估计值xk|k和协方差矩阵Pk|k。UKF滤波的递推过程为
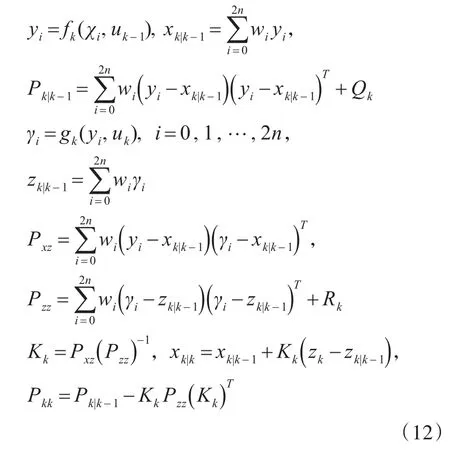
4.2 UKF-GM-PHD滤波器
下面给出UKF-GM-PHD滤波器的预测和更新方程。
1)UKF-GM-PHD预测方程
假定k-1时刻,多目标PHD函数为
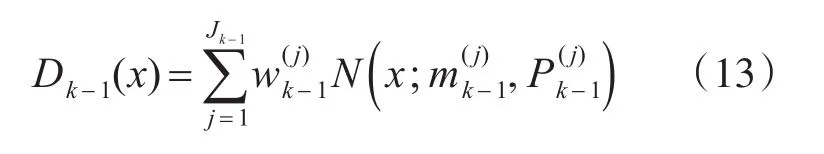
选取2n+1个加权sigma采样点{χl,wl} ,l=0,1,…,2n其选取形式与式(11)相同。
通过UKF进行线性化得到目标转移函数fk(·)的特征参数为
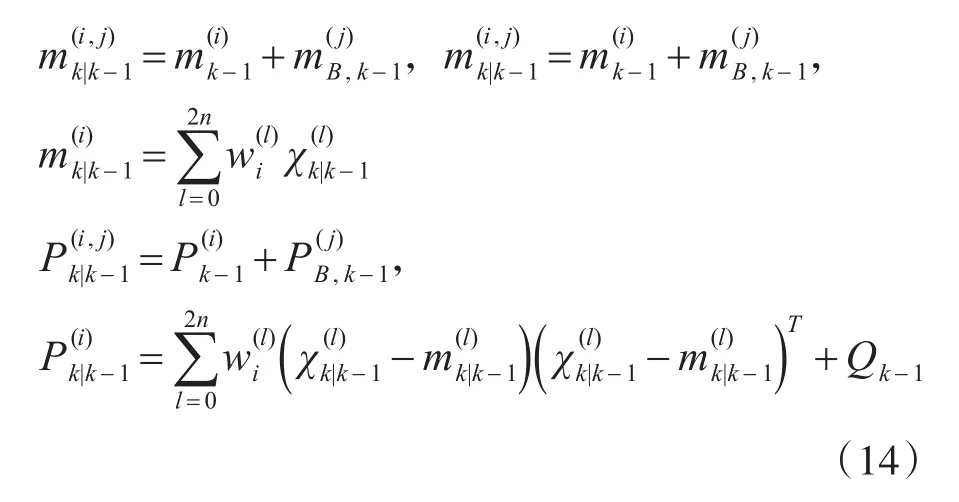
根据GM-PHD预测方程,得到UKF-GM-PHD算法的预测方程为
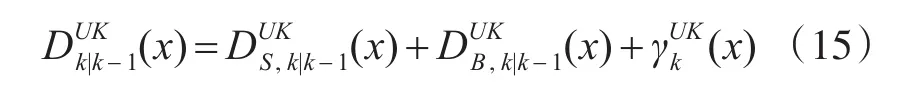
由此可得到UKF-GM-PHD滤波器的预测方程GM形式为
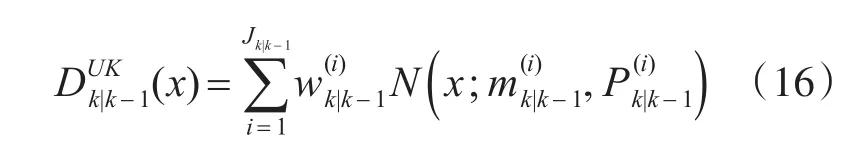
2)UKF-GM-PHD更新方程
通过U变换得到非线性量测方程gk()·的预测为
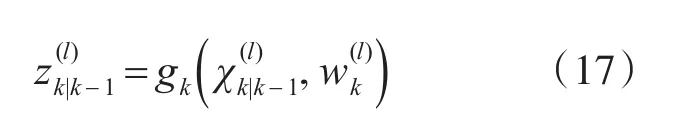
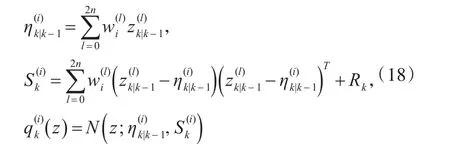
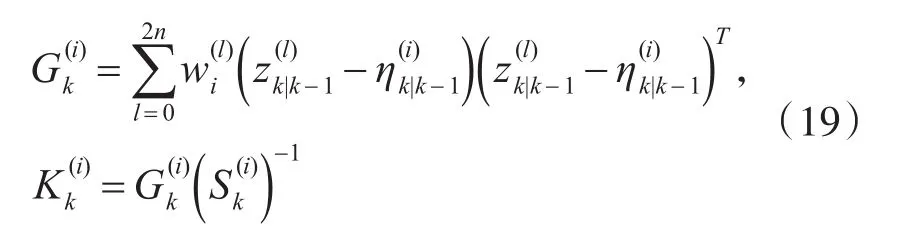
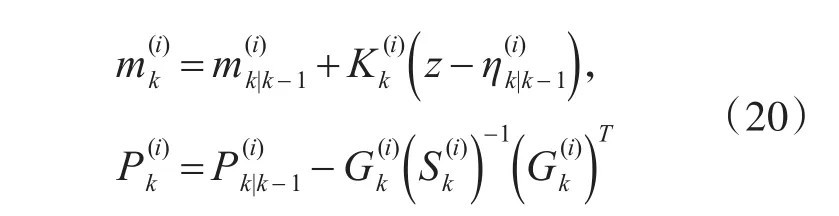
根据GM-PHD更新方程,可得到UKF-GM-PHD滤波器的更新方程为
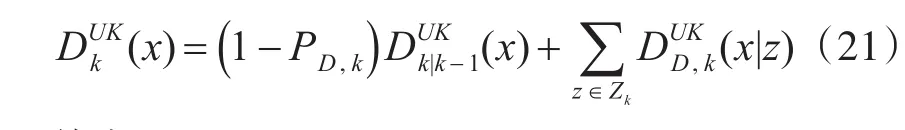
其中:
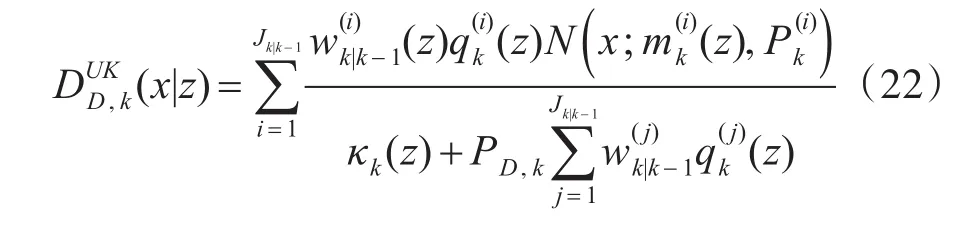
5 仿真分析
为更好验证提出的UKF-GM-PHD算法的滤波精度,将EKF-GM-PHD滤波算法与提出算法进行对比。
5.1 仿真参数设定
监控时间40s,采样间隔时间T=1s。3个目标的初始状态分量x0,P0,w0分别为
表1是3个目标的出现时刻、存活时间、消失时刻,以及目标做CV、CT和CA运动模型时刻表。

表1 3个目标的运动模型时刻表
5.2 仿真结果分析
图1是目标在非线性系统的真实轨迹和量测图。图2为GM-PHD算法的位置估计图。图3为EKF-GM-PHD算法的位置估计图。图4为UKF-GM-PHD算法的位置估计图。从三种算法的位置估计图可以明显看出,GM-PHD滤波算法在非线性系统中已失效,而其他两种算法可以实现较好的目标跟踪,验证了两种非线性处理方法在GM-PHD滤波算法上应用是有效的。
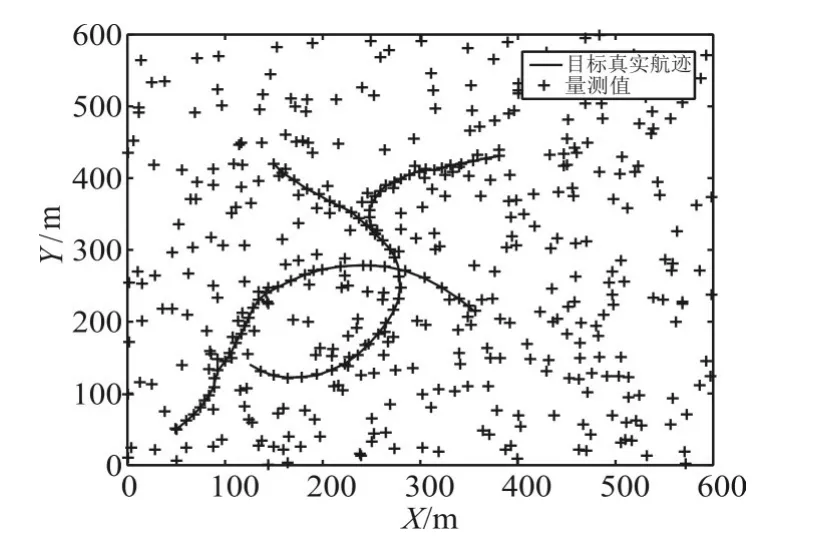
图1 目标的真实航迹和量测图
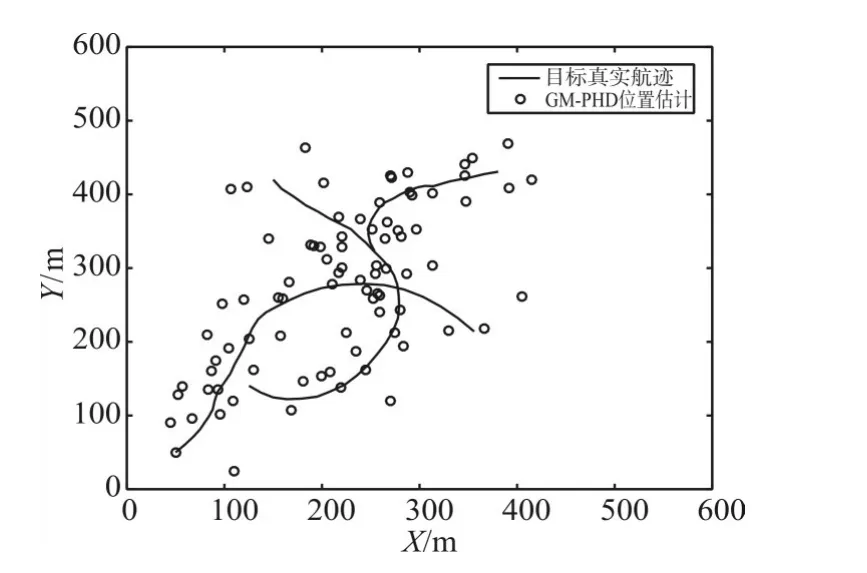
图2GM-PHD位置估计
图5和图6分别是三种算法在目标数目估计和OSPA距离的对比图。在图5中可以看到,在40s的监控时间内,GM-PHD、EKF-GM-PHD算法和UKF-GM-PHD算法丢失目标次数分别是14次、5次、1次。因此,EKF-GM-PHD算法和UKF-GM-PHD算法在监控时间段内完成了较好的跟踪滤波,但后者目标丢失率更低。从图5可以明显看出,在OSPA距离误差方面,EKF-GM-PHD算法和UKF-GM-PHD算法较GM-PHD算法很大程度上减小了误差,同时UKF-GM-PHD算法的误差比EKF-GM-PHD算法的误差小,滤波效果更好。
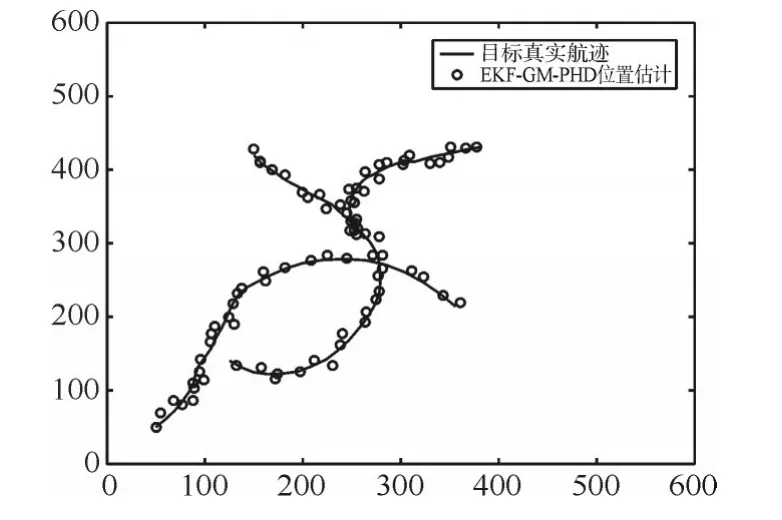
图3EKF-GM-PHD位置估计
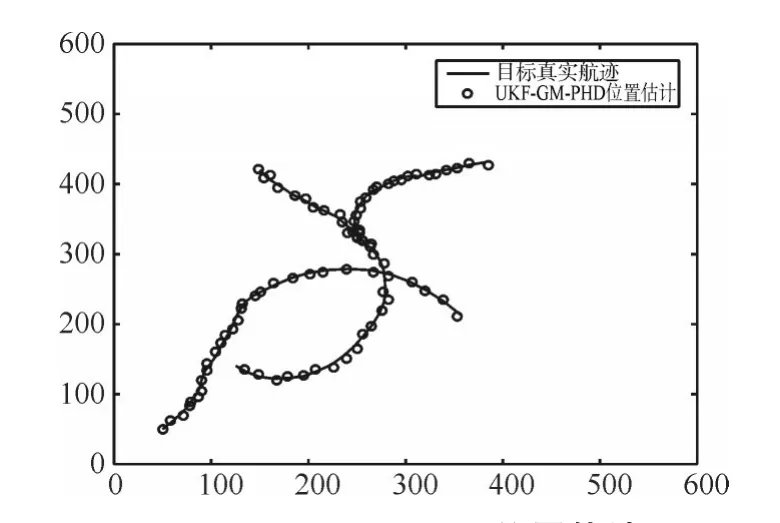
图4UKF-GM-PHD位置估计
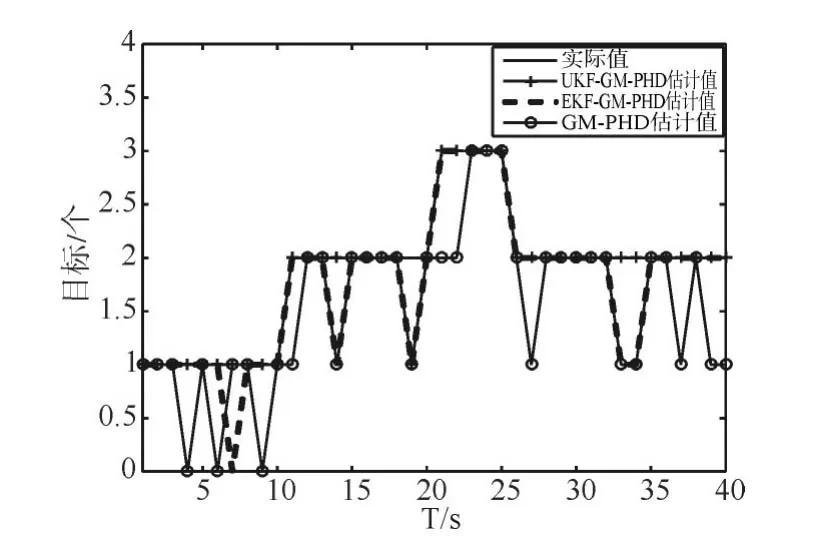
图5 目标数目估计
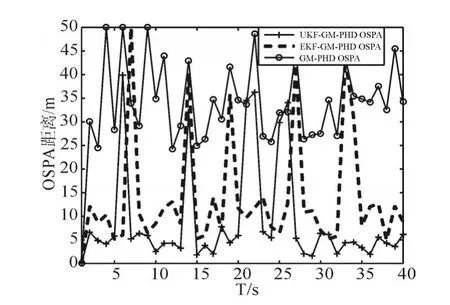
图6 OSPA距离
表2为三种算法在运行时间、目标丢失率和OSPA距离均值三方面的对比数据。表3为三种算法100次Monte Carlo仿真实验,在算法运行时间、目标丢失率和OSPA距离均值三方面的对比数据。
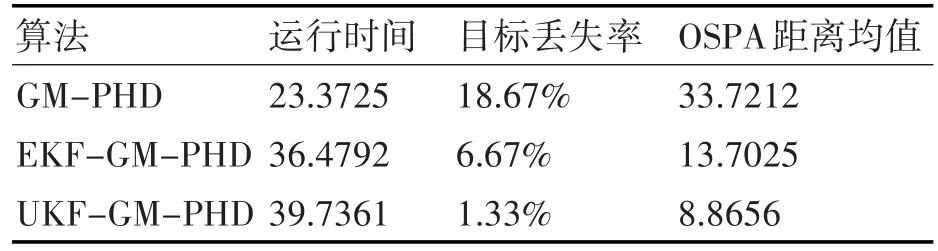
表2 三种算法数据对比
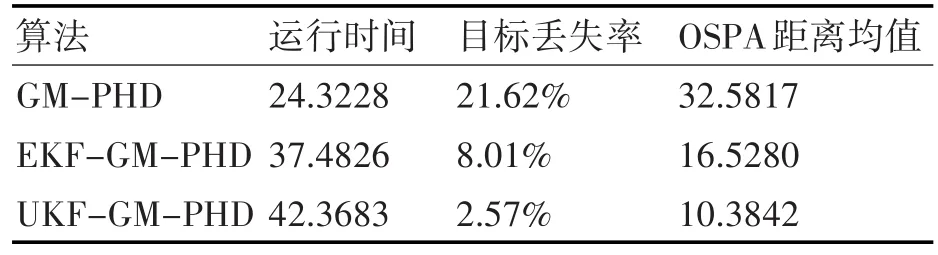
表3 100次Monte Carlo实验数据对比
从表2和表3数据对比来看,EKF-GM-PHD算法和UKF-GM-PHD算法在运行时间上相差不大,与GM-PHD算法相比,算法运行时间有了一定的增加,但在目标丢失率和OSPA距离误差上,都有了显著的提高。UKF-GM-PHD算法相对EKF-GM-PHD算法,算法运行时间相差并不大,而目标丢失率相对较低,同时OSPA距离误差也相对较小,滤波效果更好。
6 结语
本文开展基于GM-PHD滤波器在非线性目标跟踪系统中的方法研究,基于GM-PHD滤波算法在进行预测和更新过程中是基于Kalman滤波原理,将传统非线性处理方法UKF与GM-PHD滤波算法相结合,提出了UKF-GM-PHD滤波算法,通过验证提出算法的有效性,仿真多机动目标运动情形,将提出算法与EKF-GM-PHD滤波算法进行分析对比,验证了提出算法具有更高的滤波精度。

