基于模糊度的姿态测量仿真与实现
张道成
(中国人民解放军91404部队,河北 秦皇岛 066200)
随着科学技术的不断发展,载体姿态的测量得到了越来越多的应用,不仅广泛地应用在民用中,而且在军事技术上也得到了很好的应用。世界上不少研究机构或者公司都对其开展了深入的研究。美国宇航局(NASA)于20世纪90年代末开展了GPS/INS组合用于航天飞机姿态测量的研究,精度要求为0.5°/m。美国斯坦福大学于20世纪90年代末在实验室也得到了0.25°/m-0.5°/m的精度[1],茅文深针对双频姿态测量算法和组合测姿开展了研究[2]。
在短基线载波相位双差观测模型中,主要考虑两组未知数,分别是基线矢量和双差整周模糊度。本文主要对模糊度中的最小二乘去相关平差法(LAMBDA)[3]开展研究。
1 参数估计模型和准则
已知双差载波相位线性观测方程的最小二乘目标函数为

(1)

为n维整数空间,R3为3维实数空间。式(1)的最小化问题可以看成带有整数约束的最小二乘问题。
上述最小二乘估计[4]的二次型目标函数可以分解为下列形式

(2)


从上面分析可以看出最小二乘解可以分为三部分,第一步求解无约束的实数解,即根据式(1),去掉N∈Zn的约束,直接通过加权最小二乘获取实数解和对应的方差-协方差矩阵,计算结果如下
(3)

(4)
(5)
2 LAMBDA算法实现步骤
针对上面的模糊度固定问题,Delft科技大学的P.J.G Teunissen博士提出了一种快速有效的模糊度固定方法——最小二乘降相关平差法(LAMBDA),它主要有两部分:模糊度条件搜索和模糊度去相关处理(又称整数Z变换)。
2.1 模糊度整数最小二乘搜索
对于式(4)的整数最小二乘问题目前没有统一的解析求解方法,目前都是通过离散搜索的方法来得以实现。具体实现为利用式(4)来构造一个n维的实数椭球搜索范围Rn,进行搜索。这个模糊度搜索椭球可以定义为

(6)
搜索空间χ2的确定,合适的χ2可以保证最优值在搜索区域内又可以保证搜索效率,所以它在搜索过程中起着重要的作用。下面介绍LAMBDA算法中χ2的确定方法。
当期望得到的模糊度候选值个数小于等于n+1时,χ2的取值方法是取浮点解的最近整数按照式(4)的目标函数计算得到的值。即先由浮点解的最近整数求的1个二次型的值,然后分别让其中一个浮点解取次整数,其他浮点解不变,可以得到n个二次型的值,这样一共得到n+1个二次型的值。如果从这n+1个数值中选取次最小的值作为χ2,这样确定的模糊度搜索椭球大小可保证至少2个,至多几个候选模糊度;同理,取第i个最小的二次型的值可以保证搜索椭球内至少有i个候选模糊度。
当期望得到的模糊度候选值个数大于n+1时,χ2的取值方法是通过计算椭球体积大小来确定,具体计算如下:
椭球区域的体积公式为

(7)
式中,Vn为体积函数
(8)
当n≥3时,体积函数可以通过Vn=2πVn-2/n等式进行循环计算,其中V1=2,V2=π。
对于确定的方差-协方差矩阵,有下列表达式
(9)

所以由式(7)得到χ2的表达式

(10)
相关实验结果证明体积En的大小也大致确定了椭球区域内所包含的候选值的数量,即En与候选值模糊度个数k有近似关系k=int(En)[5],当k≥10时,该式较准确;但当k<10时,该式误差比较大。
2.2 模糊度去相关处理
由于模糊度浮点解之间存在着很大的相关性,使得式(6)进行模糊度搜索时效率非常低,为了避免这种情况,LAMBDA算法中加入了对模糊度浮点解进行去相关处理的方法,其基本思想为利用一个整数变换矩阵Z对模糊度以及它的协方差矩阵进行线性变换,使变换后的模糊度和其协方差矩阵相关性变弱,具体体现在由式(7)构成的搜索椭球空间规则化,从而使搜索效率提高。
2.2.1 模糊度搜索停滞现象
理论和数值分析均表明,存在着突变,为了从理论上解释突变现象,以二维模糊度的方差-协方差矩阵为例进行阐述。同时,这个二维矩阵的结构和n维的模糊度方差-协方差矩阵的内部结构相似。

(11)
假设
(12)
注意到式(11)被分解成两个秩分别为1和2的矩阵和的形式。式(12)存在的目的是使秩为2的矩阵中的元素远小于秩为1的矩阵中的元素。

(13)


(14)
同样,n维模糊度方差-协方差矩阵也可以写成两个矩阵和的形式。第一个矩阵的秩为n,同时由于载波相位观测值的精度较高,所以对应的元素值都很小。第二个矩阵的秩为3,原因是模糊度值为实数值时,估计得到的基线精度较低,所以对应的元素值都很大。由于这种结构的原因,实际上的模糊度条件方差的变化范围在第三个之后都显得很大的突变性。图1是文献[6]为例计算得到的各个模糊度的条件方差的分布图。

图1 12维条件方差取值范围
很显然,前3个和后9个模糊度条件方差之间有很大的突变,所以消除模糊度条件方差的这种突变性对于搜索效率非常重要,下面介绍的整数Z变换就是为降低这种条件方差的突变性而提出的。
2.2.2 模糊度去相关(整数Z变换)


(15)
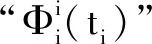

(16)

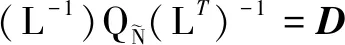
(17)
由于D为对角矩阵,所以变换后的模糊度完全不相关,但是实际中,由于模糊度的整数特性,不可能完全去相关,即取Z=int(L-1),这样D就不是对角矩阵,但非对角元素经过这样变换后一般都变得很小,有时还要经过多次这样的变换得到Z矩阵。

3 仿真分析
1) 模糊度去相关前后搜索空间的比较
这里我们采用二维模糊度作为例子,数据为文献[4]中第100页的相关数据。

(18)
经过高斯整数变换后的模糊度和对应协方差矩阵为:

(19)
显然,去相关后的模糊度对应的方差明显比变换前小,而且两者之间相关性也减弱。具体结果见图2。
其中,图2a为变换前的搜索空间,图2b为变换后的搜索空间,可以看出,变换前的空间被压缩的很狭长,N1和N2要经过很长搜索时间才能遍历所有可能整数,而对搜索空间图2b显然更容易搜索。所以整数Z变换极大提高了搜索效率。
2) 模糊度去相关前后条件方差比较
采取12维模糊度协方差矩阵,具体条件方差见图3。
从图3中可以看出,去相关后的模糊度条件方差很小并且都在同一数量级,很好的平滑了原始模糊度条件方差突变现象,从而提高了搜索效率。

图2 变换前后搜索区间比较

图3 去相关前后模糊度条件方差比较
4 结束语
本文对模糊度解算算法中的LAMBDA算法进行了详细的分析和研究,分析了参数估计模型和准则,该模型中包括基线向量和模糊度向量两组未知参数。由于模糊度的整数特性,使得模糊度的整数解没有统一的解析公式,只能通过有效的搜索方法来得到。LAMBDA算法提出了一种序贯条件最小二乘整数搜索,然而由于模糊度间的强相关性使得搜索椭球空间极其狭长,导致搜索效率很低,甚至会出现停滞现象,所以LAMBDA算法还提供了降低模糊度相关性的整数Z变换,文中给出了整数高斯Z变换的实现步骤,通过Z变换后的模糊度搜索效率大大提高从而达到实时求解的目的。

