具幂零鞍点的Hamilton系统的周期环域的环性

李慧敏, 张二丽

(郑州财经学院 信息工程学院, 河南 郑州 450001)

1 主要结果

1900年,德国数学家Hilbert在第二届国际数学家大会上提出了著名的23个数学问题,其中第16个问题的后半部分是:对于平面n次实多项式系统

其中Fn(x,y)和Gn(x,y)是n次实多项式.它可能具有的极限环个数的最小上界是多少?这些极限环的相对位置如何?最近几十年,数学工作者对该问题进行了广泛的研究[1-5].1977年,前苏联数学家Arnold提出:对平面Hamilton系统的扰动系统

(1)

其中,0<|ε|≪1,H(x,y)是关于x和y的m次实多项式,f(x,y)和g(x,y)是关于x和y的n次实多项式.假设系统(1)的未扰动系统(1)ε=0有连续闭轨线族{Γh},Σ为h的最大存在开区间,即Γh={(x,y)∈R2|H(x,y)=h,h∈Σ}.系统(1)的一阶Melnikov函数为

M(h)=∮Γhg(x,y)dx-f(x,y)dy,

h∈Σ,

(2)

问M(h)的孤立零点的最大个数是多少(计重数)?该问题称为弱Hilbert 16问题[6].相关的研究很多,详见文献[7-13].由Poincaré-Pontryagin定理[14]可知,当M(h)≠0时,系统(1)在未扰动系统(1)ε=0的闭轨线族{Γh}形成的紧致区域内产生的极限环个数(计重数)不超过M(h)的孤立零点的最大个数(计重数).

本文研究Hamilton函数

2x2y2-x4+y4

(3)

相应的向量场

(4)

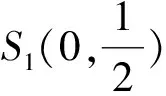
(5)

图 1 系统(4)的相图

定理 1.1对任意0<|ε|≪1和n次实多项式f(x,y)与g(x,y),当n≥5时,扰动系统(5)至多存在4n+10个极限环;当n=3,4时,扰动系统(5)至多存在9个极限环;当n=1,2时,扰动系统(5)不存在极限环.

2 一阶Melnikov函数M(h)和Picard-Fuchs方程

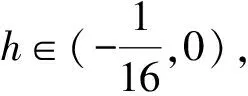
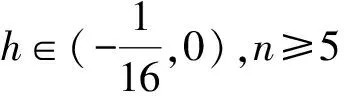
M(h)=α(h)I0,1+β(h)I0,3+

γ(h)I2,1+δ(h)I2,3,

(6)

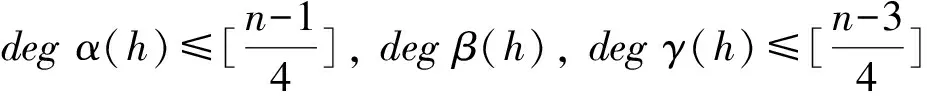
证明因为Γh关于x-轴和y-轴对称,所以Ii,2j=I2i+1,2j+1≡0.由Green公式可得

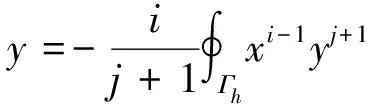
所以

其中τij是常数.

对H(x,y)=h两端同时关于x求导可得

(7)

其中H(x,y)由(3)式定义.(7)式两端同乘以xi-3yjdx并沿着Γh积分可得

(8)

(3)式两端同时乘以xiyj-4dx,并沿着Γh积分可得

(9)

由(8)和(9)式可得

(10)

(11)

下面用数学归纳法证明结论成立.当n=5,7时,由(10)和(11)式可得

所以当n=5时结论成立.假设当i+j≤2k-1(k≥3)时结论成立.当i+j=2k+1(k≥2)时,在(10)式中取(i,j)=(0,2k+1),(1,2k),(2,2k-1),…,(2k-3,4),在(11)式中取(i,j)=(2k-2,3),(2k-1,2),(2k,1)可得

其中

是k+1阶方阵.计算可得detA=2,所以

因此

同理可得

证毕.

引理 2.2记V=(I0,1,I0,3,I2,1,I2,3)T,则V满足Picard-Fuchs方程

(Bh+C)V′=V,

(13)

其中

证明对H(x,y)=h两端同时关于h求导可得

其中H(x,y)由(3)式定义,所以

(14)

进而可得

(15)

(14)式两端同乘以h并注意到(3)式可得

(16)

(17)

由(15)～(17)式可得

(18)

在(18)式中分别取(i,j)=(0,1),(0,3),(2,1)和(2,3)可得

注意到(10)和(11)式可得结论成立.证毕.

引理 2.3令

(19)

则I01、I03、I21和Z满足

(20)

其中

证明对(13)式两端关于h求导得

(Bh+C)V″=(I-B)V′,

其中I是4×4阶单位矩阵.假设

本文是在南阳理工学院软件学院《软件工程》课程基础上，实施OBE工程教育模式的经验总结。基于OBE教学模式定义软件工程课程目标，学生学习软件项目开发过程，掌握软件开发的主流方法，了解软件开发过程中应遵循的原则、标准、规范和流程，在项目开发过程中，培养科学的思维方法，灵活运用知识的能力，养成良好的编程习惯，积累软件项目开发经验，为学生职业能力培养和职业综合素质培养起重要支撑作用。

G(h)V″=(Bh+C)*(I-B)V′=

(21)

其中G(h)=det(Bh+C),(Bh+C)*表示矩阵Bh+的伴随矩阵.由(21)式可得(20)式成立.证毕.

由(3)和(4)式可得

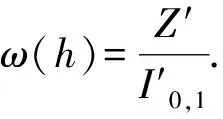
G(h)ω′(h)=-σ12(h)ω2(h)+

(σ42(h)-σ11(h))ω(h)+σ41(h).

(22)

证明由(20)式的第一个和第四个方程即可得(22)式成立.引理得证.

3 定理1.1的证明

(i) 由(6)、(13)和(19)式可得

(23)

其中,αs(h)、βs(h)、γs(h)和δs(h)是关于h的多项式,且满足:

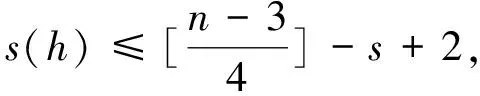
γ1(h)M′(h)=γ2(h)M(h)+F1(h),

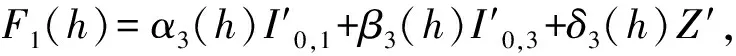
由文献[15]中引理5.1可得

#{M(h)=0}≤#{γ1(h)=0}+

#{F1(h)=0}+1≤

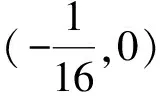
其中

(24)

其中

(25)

所以

由文献[9]中引理4.2可得

{#F1(h)=0}≤#{β3(h)=0}+

#{F2(h)=0}+1≤

(26)

其中

由文献[9]中引理4.4可得

{#R0(h)=0}+{#δ4(h)=0}+1≤

综合(i)～(iii)可得

#{M(h)=0}≤

再由Poincaré-Pontryagin定理可知,当n≥5时,系统(5)至多有4n+10个极限环.

当n=1,2时,M(h)=λ0I01(h),其中λ0是非零常数.因为

I01(h)=∮Γhydx=-∬Ddxdy≠0,

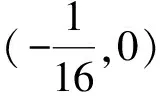
当n=3,4时,M(h)=λ1I01+λ2I03+λ3I21,其中λ1、λ2和λ3是常数.由(19)和(20)式可知

其中

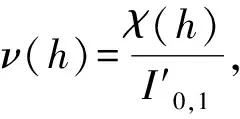
G(h)λ5(h)ν′(h)=-σ12(h)ν2(h)+

λ6(h)ν(h)+λ7(h),

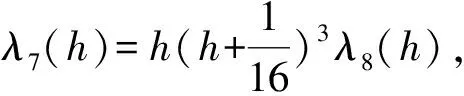
#{M″(h)=0}=#{χ(h)=0}=#{ν=0}≤

#{λ5(h)=0}+#{λ7(h)=0}+1≤8.

又I(0)=0,所以#{M(h)=0}≤9.定理1.1证毕.