圆锥曲线等效判别式及其应用

北京市育英学校(100036) 牛文政

北京市昌平区大东流中学(102211) 王素文

一、等效判别式

在研究直线与圆锥曲线的位置关系时,为了使直线与曲线的位置关系问题更易于处理,我们选用直线的一般式与有心圆锥曲线联立,可以得到相应一元二次方程的等效判别式,其形式优美,并且在处理相切问题时比较有效.

1.1 有心圆锥曲线的等效判别式

命题1当m2A2+n2B20时,设直线l:Ax+By+C=0(A2+B2/=0),有心圆锥曲线=1(其中m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数),记,则

(1)直线l与有心圆锥曲线Γ相切⇔Δc=0;

(2)直线l与有心圆锥曲线Γ相交⇔Δc＞0;

(3)直线l与有心圆锥曲线Γ相离⇔Δc＜0.

我们有以下定义:

定义1当m2A2+n2B20时,叫做直线l:Ax+By+C=与有心圆锥曲线=1(其中m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数)联立所得一元二次方程的有心圆锥曲线的等效判别式.

1.2 抛物线Γ:y2=2px(p0)的等效判别式

命题2设直线l:Ax+By+C=0(A2+B2/0),抛物线Γ:y2=2px(p0),当A/0时,

(1)直线l与抛物线Γ相切⇔Δp1=

(2)直线l与抛物线Γ相交⇔Δp1=

(3)直线l与抛物线Γ相离⇔Δp1=

当A=0时,直线l与抛物线Γ有且只有一个交点.

定义2当A/0时,叫做直线与抛物线Γ:y2=2px(p0)联立所得一元二次方程的抛物线Γ:y2=2px(p/0)的等效判别式.

1.3 抛物线Γ:x2=2py(p0)的等效判别式

命题3设直线l:Ax+By+C=0(A2+B2/0),抛物线Γ:x2=2py(p/0),当B0时,

(1)直线l与抛物线Γ相切⇔Δp2=

(2)直线l与抛物线Γ相交⇔Δp2=

(3)直线l与抛物线Γ相离⇔Δp2=

当B=0时,直线l与抛物线Γ有且只有一个交点.

定义3当B/0时叫做直线与抛物线Γ:x2=2py(p0)联立所得一元二次方程的抛物线Γ:x2=2py(p0)的等效判别式.

圆锥曲线等效判别式是变量的对应系数相乘平方的代数和,形式优美、简洁、和谐.运用等效判别式,我们可以得到圆锥曲线的弦长公式与圆锥曲线的焦点弦长公式,并举例说明它们的应用.

二、等效判别式的应用

2.1 有心圆锥曲线的弦长公式

运用椭圆的等效判别式,可得到有心圆锥曲线的弦长公式:

命题4当m2A2+n2B20时,若直线l:Ax+By+C=0(A2+B2/0)与有心圆锥曲线(其中m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数)相交于不同两点P,Q,则有有心圆锥曲线的弦长公式(一):

证明设P(x1,y1),Q(x2,y2),将直线l代入有心圆锥曲线Γ,化简整理得:当时,其中则则

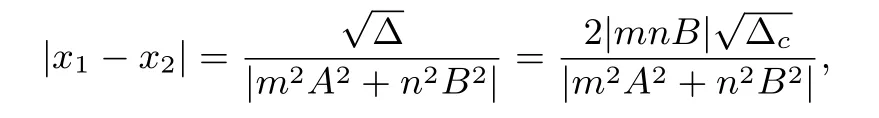
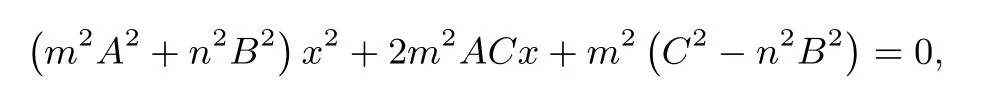
则

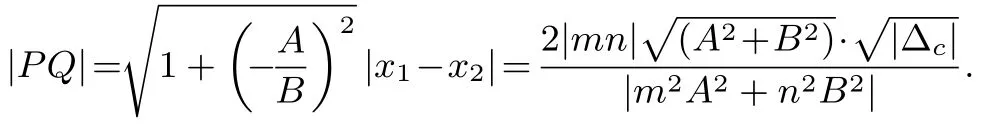
当B=0时,可以验证满足上式.证毕.

情形1若直线l:Ax+By+C=0 (A2+B20)与椭圆=1(a,b＞0,ab)相交于不同两点P,Q,则有椭圆标准方程的弦长公式(二):

圆可以看作特殊的椭圆,根据圆的等效判别式,可得到圆的弦长公式:

情形2若直线l:Ax+By+C=0(A2+B20)与圆Γ:x2+y2=r2相交于不同两点P,Q,则有圆的弦长公式(三):

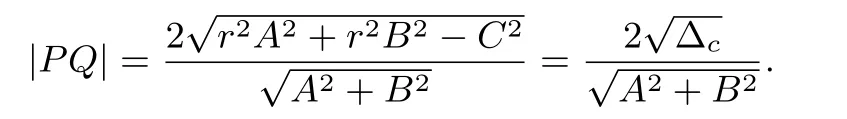
情形3若直线l:Ax+By+C=0与双曲线=1(a,b＞0)相交于不同两点P,Q,则有焦点在x轴上的双曲线标准方程的弦长公式(四):

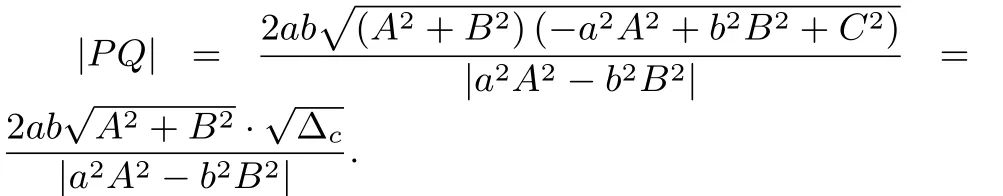
情形4若直线l:By+Ax+C=与双曲线相交于不同两点P,Q,则有焦点在y轴上的双曲线标准方程弦长公式(五):

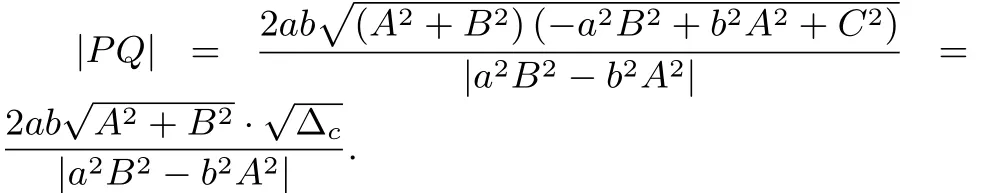
当直线过圆锥曲线焦点时,其焦点弦长公式如下:

推论1当m2A2+n2B2/0时,若直线l:Ax+By+C=0(A2+B2/0)与有心圆锥曲线(其中m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数)相交于不同两点P,Q,则有有心圆锥曲线的焦点弦长公式(六):

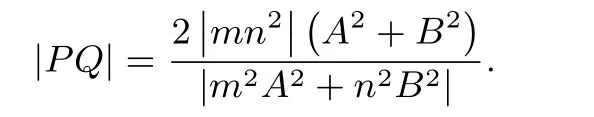
上面公式中,圆锥曲线退化为圆时,焦点弦退化为直径.

情形5若直线l:Ax+By+C=0过椭圆的焦点,与椭圆Γ相交于不同两点P,Q,则有椭圆标准方程的焦点弦长公式(七):

情形6若直线过双曲线=1(a,b＞0)的焦点,与双曲线Γ相交于不同两点P,Q,则有焦点在x轴上的双曲线标准方程的焦点弦长公式(八):

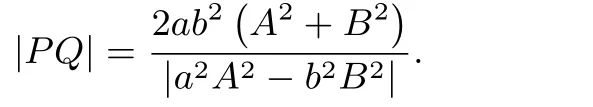
情形7若直线过双曲线=1(a,b＞0)的焦点,与双曲线Γ相交于不同两点P,Q,则有焦点在y轴上的双曲线标准方程的焦点弦长公式(九):

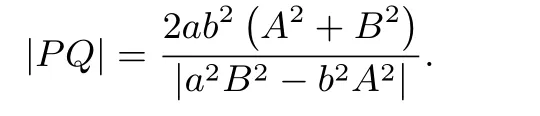
2.2 抛物线的弦长公式

命题5当A0时,若直线l:Ax+By+C=0(A2+B20)与抛物线Γ:y2=2px(p0)交于不同两点P,Q,则有抛物线Γ:y2=2px(p/0)的弦长公式(十):

命题6当B0时,若直线l:Ax+By+C=0(A2+B2/0)与抛物线Γ:x2=2py(p0)交于不同两点P,Q,则有抛物线Γ:x2=2py(p/0)的弦长公式(十一):

推论2当A0时,若直线l:Ax+By+C=0(A2+B2/0)与抛物线Γ:y2=2px(p0)交于不同两点P,Q,则有抛物线Γ:y2=2px(p/0)的弦长公式(十二):

推论3当B0时,若直线l:Ax+By+C=0(A2+B20)与抛物线Γ:x2=2py(p0)交于不同两点P,Q,则有抛物线Γ:x2=2py(p0)的弦长公式(十三):

三、等效判别式的应用举例

3.1 等效判别式对蒙日圆的证明

在椭圆中,任意两条互相垂直的切线的交点都在同一个圆上,它的圆心是椭圆中心,半径等于长半轴与短半轴平方和的算数平方根,这个圆叫蒙日圆,是法国数学家、画法几何的创始人G.Monge(1745-1818)最先发现的,单墫教授将其命名为准圆.

文[1]给出了两种解析几何、两种平面几何证明方法.文[2]给出了一种平面几何证明方法,并得到了其逆命题.以下命题7-10,12,13出现在文[1],[2],[3]中.下面我们运用等效判别式,给出一种新的代数证明,进而得到其统一形式的命题及证明.

命题7椭圆(a,b＞0,a/b)的两条互相垂直的切线的交点P的轨迹是圆x2+y2=a2+b2.

命题8过圆x2+y2=a2+b2上任意点P作椭圆=1 (a,b＞0,ab)的两条切线,则两条切线相互垂直.

命题9双曲线=1 (a＞b＞0)的两条互相垂直的切线的交点P的轨迹是圆x2+y2=a2-b2.

命题10过圆x2+y2=a2-b2上任意点P作双曲线=1(a＞b＞0)的两条切线,则两条切线相互垂直.

对于焦点在y轴上的双曲线,也有类似命题:

命题11双曲线(a＞b＞0)的两条互相垂直的切线的交点P的轨迹是圆x2+y2=a2-b2.

命题12过圆x2+y2=a2-b2上任意点P作双曲线=1(a＞b＞0)的两条切线,则两条切线相互垂直.

命题13当m2+n2＞0时,有心圆锥曲线Γ:=1(其中m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数)的两条互相垂直的切线的交点P的轨迹是圆x2+y2=m2+n2.

证明(1)设点P(x0,y0),两条互相垂直的切线分别为:l1:Ax+By+C=0(A2+B20)与l2:Bx-Ay+C1=0,由命题1,知

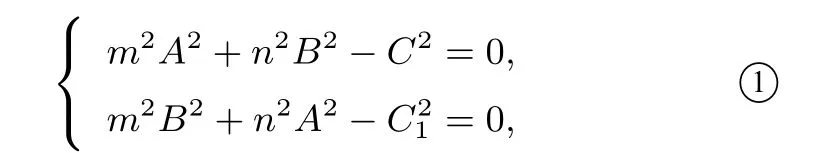
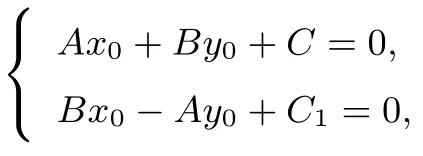
(2)在圆x2+y2=m2+n2上任取点P1(x1,y1),则,过P1作曲线Γ的一条切线l3:Dx+Ey+F=0 (D2+E20),则由命题1,知m2D2+n2E2=F2.过P1作l3的垂线l4:Ex-Dy+F1=0,下面我们证明直线l4与曲线Γ相切:由两式相加得:则()()则m2E2+n2(-D)2-F21=0,由命题1知,l4与椭圆Γ相切,即过圆x2+y2=a2+b2上任意点P1作椭圆Γ的两条切线互相垂直.

由(1),(2)可知,命题13得证.

当m2+n2＞0时,若m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数时,圆x2+y2=m2+n2就是单墫教授曾命名的(外)准圆.

在上述证明中,其实蕴含了命题13的逆命题:

命题14过圆x2+y2=m2+n2(m,n＞0;或m＞0,n为实数或纯虚数;或n＞0,m为实数或纯虚数)上任意点P作有心曲线的两条切线,则两条切线相互垂直.

对于抛物线,有以下命题:

命题15抛物线的两条互相垂直的切线的交点P的轨迹是该抛物线的准线.

证明不妨设抛物线Γ:y2=2px(p0).

(1)设点P(x0,y0),两条互相垂直的切线分别为:l1:Ax+By+C=0 (A2+B20)与l2:Bx-Ay+C1=0,由命题2知:两式相加得:=2(AC+BC1),又点P(x0,y0)在l1,l2上,有则(A2+B2)x0+AC+BC1=0,则即抛物线Γ的两条互相垂直的切线的交点P都在准线上.

在上述证明中,其实蕴含了命题15的逆命题:

命题16过抛物线的准线上任意点P作抛物线的两条切线,则两条切线相互垂直.

3.2 等效判别式的应用举例

例1(2016年高考全国新课标理科II卷)已知椭圆的焦点在x轴上,A是E的左顶点,斜率为k(k＞0)的直线交E于A,M两点,点N在E上,MA⊥NA.(I)当t=4,|AM|=|AN|时,求△AMN的面积;(II)当2|AM|=|AN|时,求k的取值范围.

解(I)(II)由题意t＞3, k＞0,直线AM:由命题4的椭圆标准方程的弦长公式(二)知,同理可得:由2|AM|=|AN|得:则故

例2设直线l:Ax+By+C=0 (A2+B2/0)与椭圆=1(a＞b＞0)交于不同两点P,Q,O为坐标原点,试证:当且仅当a2A2+b2B2=2C2时,△OPQ有最大面积

证明由命题4知,

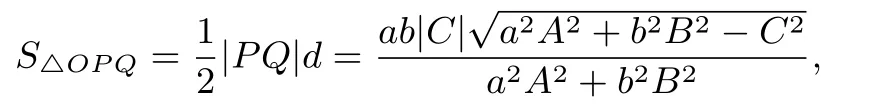
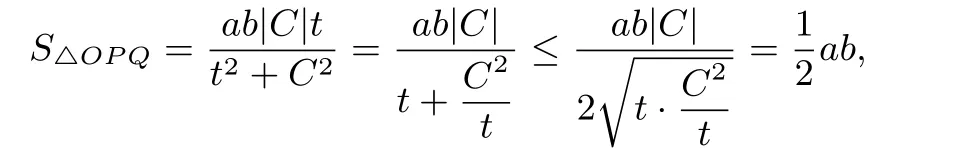
例3(2007武汉大学自主招生试题)过抛物线Γ:y2=8x上一点P(2,4)作倾斜角互补的两条直线,分别与抛物线交于A,B两点,(I)求直线AB的斜率;(II)如果A,B两点均在y2=8x(y≤0)上,求△PAB面积的最大值.

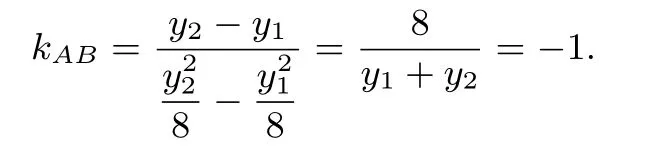
(II)设直线AB的方程为:x+y+C = 0,由A,B两点均在y2= 8x(y ≤ 0)上及命题2,得即C∈[0,2),由命题5,

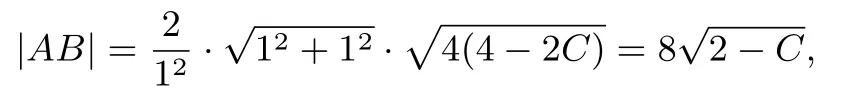
圆锥曲线的等效判别式,形式优美,应用广泛.其实不需要记忆,使用时用直线的一般方程与圆锥曲线联立,很快能推导得到字母表达形式,再加以运用,有时会有很好的效果.