浅谈利用极限思想分析函数图像

郑鹏

【摘 要】极限思想不仅仅局限于大学数学分析等高等数学中的应用，在高中的函数及其图像问题中，也起到了很重要的作用。

【关键词】极限思想;函数图像;趋近于;变化趋势

“极限”是数学中的分支——微积分的基本概念，广义的“极限”是指：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”的过程中，此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的指A就叫做“极限值”。这是百度百科对“极限”一词的描述。极限的英文名叫“limit”，在数学中的符号就是“lim”，主要应用于微积分。

而所谓极限思想，其实就是用极限的概念分析问题和解决问题的一种数学思想。这是微积分的基本思想，在大学数学分析这门课中，如函数连续性、导数以及定积分等等都是借助于极限来定义的。

用极限思想解决问题的一般步骤就是：对于被考察的未知量，先设法正确地构思一个与它的变化有关的另外一个变量，确认此变量通过无限变化过程的“影响”趋势性结果就是非常精密的约等于所求的未知量;用极限原理就可以计算得到被考察的未知量的结果。与一切科学的思想方法一样，极限思想也是社会实践的大脑抽象思维的产物。极限思想可以追溯到古代，例如，刘徽“割圆术”就是建立在直观图形研究基础上的一种原始可靠的“不断靠近”的极限思想的应用。

那么在数学史中占据如此重要地位的极限思想，是否仅用于大学数学分析等高等数学中的研究呢？它在我们高中数学教学中又有哪些重要的应用，就是我想阐述的本篇文章中我个人对极限思想在高中数学中的应用，尤其是在函数及其图像中的应用。

在高中数学的函数内容学习中，函数单调性是函数最重要的一个性质，等同于一个函数的灵魂，有了单调性，我们就把握住了一个函数的命脉，知道了它的走向。我们利用导数来分析函数单调性，有了单调递增和单调递减，或者恒等于某个值，这些都是我们可以通过函数的导数得到的。但是知道了一个函数单调性，我们离画出一个函数图像还存在一个难点，就是从哪开始，又到哪结束。这就好比于我们知道了一个函数走向，可是从哪走到哪我们并不清楚，画出的图像也是存在问题的。

用一个最简单的我们最熟悉的函数来看：反比例函数，我们通过求导发现，导数，是恒小于零的，意味着是一直單调递减的，那我们是否在定义域上就画出一条递减的曲线呢？那我们在画出它的图像中，还存在一个难点，就是从哪递减到哪，这也就是很多学生困惑的地方。虽说大家都对反比例函数图像很了解，但是为什么长这样，大部分同学还是停留在初中对它利用描点法画出的图像上。那么我们的极限思想，在这就对函数图像有一些新见解。我们发现，当值无限趋近于时，值仍然是正数，且接近于0;当值无限趋近于0但仍然为正数时，值就会趋近于。而在区间上，导数又是一直小于零的，所以我们能分析出来，这个函数在上单调递减，而且是从开始一直递减到接近0的，且一直为正数。

同样道理，在上，当值无限趋近于时，等于将会变成一个无限靠近0的负数;当值无限趋近于0且为负数时，值就会趋于。所以这个函数在上也是单调递减，而且是从接近0的负数开始一直递减到的，且一直为负数。

那么如此我们针对的图像就有了大概的形状，当然，这只是对一个简单函数的应用，极限思想的厉害之处不仅于此，我们来看一下下面一些题型，感受下极限思想的重要之处。

例1：函数的大致图像是（ ）

这种函数图像的问题是高考热点题型，对于这个函数，我们发现它并没有奇偶性，求导分析又过于复杂，也没有任何一个特殊值的位置，那么分析起来就存在一定的难度，这时候我们可以借助极限思想来分析函数，当值从右边无限趋近于0时，即无限趋近于0且为正数时，分子为正数，也为正数，则为正数。所以排除选项。当无限趋近于时，分子为正数，也为正数，但是指数函数相对于二次函数来说增长性是最强的，（当无限趋近于时，函数增长性：指数函数>三次函数>二次函数>一次函数>对数函数），所以分母相对于分子来说特别地大，则函数值将会无限趋于0且为正数，则能选出正确选项。

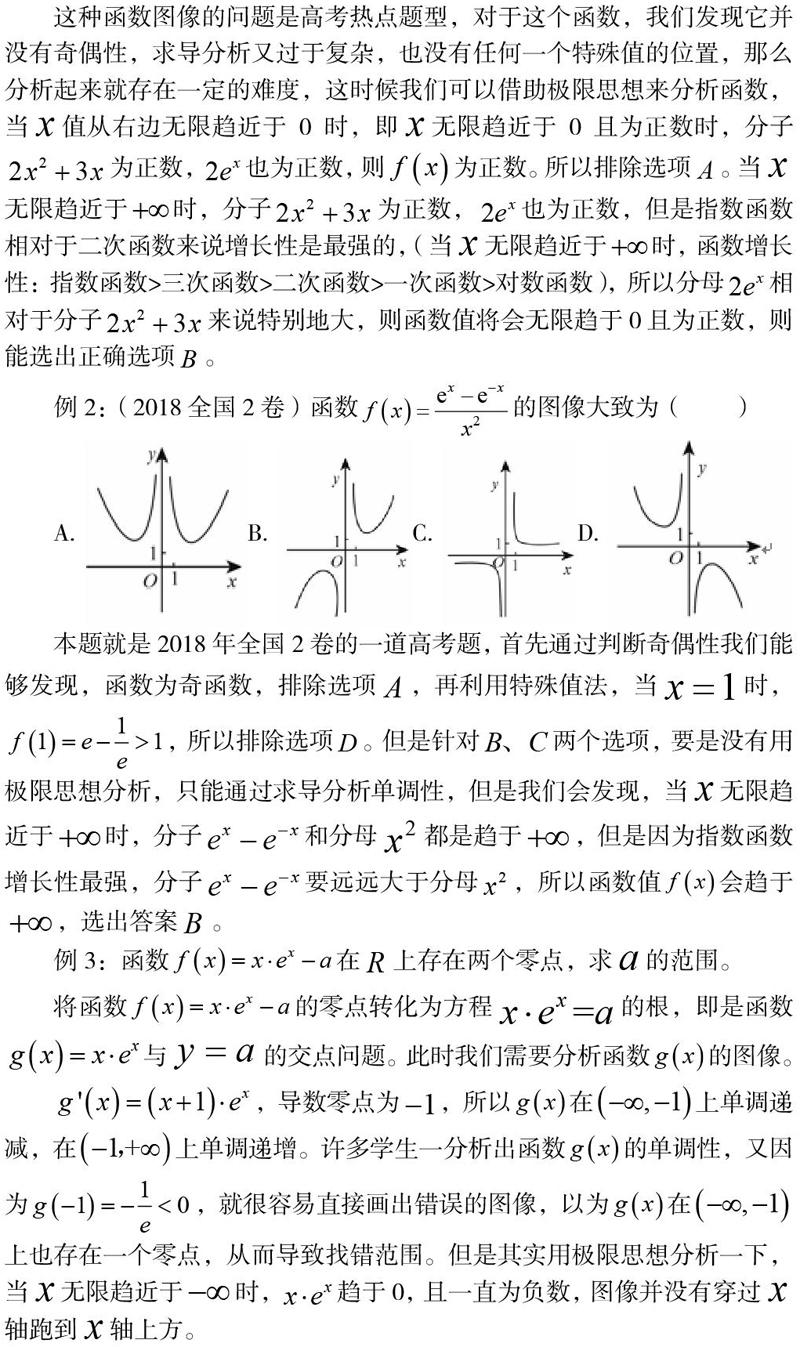
例2：（2018全国2卷）函数的图像大致为（）

本题就是2018年全国2卷的一道高考题，首先通过判断奇偶性我们能够发现，函数为奇函数，排除选项，再利用特殊值法，当时，，所以排除选项。但是针对两个选项，要是没有用极限思想分析，只能通过求导分析单调性，但是我们会发现，当无限趋近于时，分子和分母都是趋于，但是因为指数函数增长性最强，分子要远远大于分母，所以函数值会趋于，选出答案。

例3：函数在上存在两个零点，求的范围。

将函数的零点转化为方程的根，即是函数与的交点问题。此时我们需要分析函数的图像。

，导数零点为，所以在上单调递减，在上单调递增。许多学生一分析出函数的单调性，又因为，就很容易直接画出错误的图像，以为在上也存在一个零点，从而导致找错范围。但是其实用极限思想分析一下，当无限趋近于时，趋于0，且一直为负数，图像并没有穿过轴跑到轴上方。

以上三道例题，充分体现了极限思想在函数的学习过程中起到了至关重要的作用。某些高考热门题型，利用极限思想就能够迅速得到答案。然而现在许多学生都只是停留在通过求导分析函数单调性的地步，某些基础好一些的同学可能能够根据某些点处的函数值大概确定函数图像，但是并不知道在无穷远这些没有边界的地方，函数是怎样变化的。所以我觉得在高中的数学教学中，将极限思想渗透到学生分析函数过程的固有思维中，能够加强学生对函数这一大块重难点的突破。

参考文献：

[1]李芳.极限思想的产生与发展[J].语数外学习（高中版中旬），2020（05）：64-66.

[2]梅永健.浅谈高中数学中的极限思想[J].语数外学习（高中版上旬），2017（06）：43.

[3]谢慧杰.极限思想的产生、发展与完善[J].数学学习与研究（教研版），2008（09）：27.

（作者单位：云南衡水呈贡实验中学）